Каким знаком обозначается расстояние в математике: S – расстояние (путь); t – время, за которое пройдено расстояние S ; v – скорость движения.». Скачать бесплатно и без регистрации.
Каким знаком пишется скорость. Урок математики: «Скорость
Эта тема будет полезна не только учащимся средней школы, но даже взрослым. Кроме того, статья будет интересна родителям, желающим объяснить своим детям простые вещи из естественных наук. Среди очень важных тем — это скорость в физике.
Довольно часто ученики не могут разобраться в решении задач, отличить имеющиеся виды скоростей, а еще сложнее понять научные определения. Здесь мы рассмотрим все на более доступном языке, чтобы было не только все ясно, но даже интересно. А вот запомнить некоторые вещи все же придется, так как технические науки (физика и математика) требуют заучивать наизусть формулы, единицы измерения и, конечно же, значения символов в каждой формуле.
Где встречается?
Для начала вспомним, что данная тема относится к такому разделу физики как механика, подразделу «Кинематика». Кроме того, изучение скорости на этом не заканчивается, оно будет и в последующих разделах:
- оптика,
- колебания и волны,
- термодинамика,
- квантовая физика и так далее.

Также понятие скорость встречается в химии, биологии, географии, информатике. В физике тема «скорость» встречается чаще всего и изучается углубленно.
Кроме того, данное слово употребляется в повседневной жизни всеми нами, особенно среди автомобилистов, водителей транспортной техники. Даже опытные кулинары иногда используют фразу, например, «взбить яичные белки миксером на средней скорости».
Что такое скорость?
Скорость в физике — это кинематическая величина. Означает расстояние, которое преодолевается телом за какой-то промежуток времени. Допустим, молодой человек движется от дома к магазину, преодолевая двести метров за одну минуту. Напротив, его старенькая бабушка пройдет тем же маршрутом за шесть минут мелкими шажками. То есть парень перемещается намного быстрее своей пожилой родственницы, так как развивает скорость гораздо больше, делая очень быстрые длинные шаги.
То же самое стоит сказать про автомобиль: одна машина едет быстрее, а другая медленнее, потому что скорости движения разные. Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.
Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.
Формула
На уроке в школе обязательно рассматривается формула скорости в физике для того, чтобы было удобно решать задачи.
- V — это, соответственно, скорость движения;
- S — расстояние, которое преодолевается телом при перемещении от одной точки в пространстве до другой;
- t — время перемещения.
Следует запомнить формулу, потому что она пригодится в будущем при решении множества задач и не только. Например, вам может стать интересно, с какой скоростью дойдете от дома до работы или места учебы. Но вы заранее можете узнать расстояние по карте в смартфоне или на компьютере, либо по бумажному варианту, зная масштаб и имея при себе линейку. Далее вы засекаете время, перед тем, как начать движение. Придя на место назначения, смотрите, сколько минут или часов потребовалось пройти без остановки.
В чем измеряется?
Скорость чаще всего измеряется по системе единиц СИ.
- км/ч (километр в час) — транспорт;
- м/с (метр в секунду) — ветер;
- км/с (километр в секунду) — космические объекты, ракеты;
- мм/ч (миллиметр в час) — жидкости.
Давайте для начала разберемся, откуда взялась дробная черта и почему единица измерения именно такая. Обратите внимание по физике на формулу скорости. Что вы видите? В числителе стоит S (расстояние, путь). В чем измеряется расстояние? В километрах, метрах, миллиметрах. В знаменателе, соответственно, t (время) — часы, минуты, секунды. Отсюда и единицы измерения величины именно такие, как представлены в начале данного раздела.
Закрепим с вами изучение формулы скорости в физике следующим образом: какое расстояние преодолеет тело за конкретный промежуток времени? Например, человек пройдет 5 километров за 1 час. Итого: скорость движения человека — 5 км/ч.
От чего зависит?
Нередко учителя задают ученикам вопрос: «От чего зависит скорость?». Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.
Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.
Во многих задачах по кинематике приходится строить графики зависимости, где по оси Х — время, а по оси Y — расстояние, путь. По таким изображениям можно легко оценить характер скорости движения. Стоит отметить, что во многих профессиях, связанных с транспортом, электрическими машинами часто применяются графики. Например, на железной дороге.
В нужный момент измеряем скорость
Есть еще одна тема, которая пугает учеников средней школы, — мгновенная скорость. В физике это понятие встречается как определение величины скорости в мгновенный промежуток времени.
Давайте рассмотрим простой пример: машинист ведет поезд, его помощник наблюдает за скоростью движения время от времени. Вдалеке виднеется Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.
Вдалеке виднеется Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.
Начало движения
Без начальной скорости физика не представляет практически ни одно движение транспортной техники. Что это за параметр? Это скорость, с которой начинает движение объект. Допустим, машина не может начинать движение моментально со скоростью 50 км/ч. Ей нужно разогнаться. Когда водитель нажимает педаль, автомобиль плавно начинает движение, например, со скоростью сначала 5 км/ч, потом постепенно 10 км/ч, 20 км/ч и так далее (5 км/ч и есть начальная скорость).
Конечно, можно совершить резкий старт, какой бывает у бегунов-спортсменов, при ударе теннисного мяча ракеткой, но все равно всегда существует начальная скорость. Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.
Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.
Равномерная скорость
Скорость в физике — это совокупность отдельных явлений и характеристик. Различают также равномерное и неравномерное движение, криволинейное и прямолинейное. Давайте приведем пример: человек идет по прямой дороге с одинаковой скоростью преодолевая из точки А в точку В расстояние 100 метров.
С одной стороны, это можно назвать прямолинейной и равномерной скоростью. Но если присоединить человеку очень точные датчики скорости, маршрута, то можно заметить, что разница все же есть. Неравномерная скорость — это когда скорость регулярно или постоянно меняется.
В быту и технике
Скорость движения в физике существует всюду. Даже микроорганизмы перемещаются, пусть и с очень медленной скоростью. Стоит отметить, что существует вращение, которое характеризуется также скоростью, но имеет единицу измерения — об/мин (обороты в минуту). Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).
Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).
В географии и химии
Даже вода имеет скорость движения. Физика всего лишь является дочерней наукой в сфере процессов, происходящих в природе. Допустим, скорость ветра, волны в море — это все измеряется привычными физическими параметрами, величинами.
Наверняка, многие из вас знакомы с фразой «скорость химической реакции». Только в химии это имеет иное значение, так как имеется в виду, за какое время произойдет тот или иной процесс. Например, марганцовка быстрее растворится в воде, если взболтать сосуд.
Скорость-невидимка
Существуют невидимые явления. Например, мы не можем видеть, как перемещаются частицы света, различных излучений, как распространяется звук. Но если бы не было движения их частиц, то никакое бы из этих явлений не существовало в природе.
Информатика
Практически каждый современный человек сталкивается с понятием «скорость» во время работы на компьютере:
- скорость Интернета;
- скорость загрузки страниц;
- быстрота загрузки процессора и так далее.

Примеров скорости движения в физике можно привести огромное множество.
Внимательно прочитав статью , вы познакомились с понятием скорости, узнали, что она из себя представляет. Пусть данный материал поможет вам углубленно изучить раздел «Механика», проявить к нему интерес и побороть страх при ответах на уроках. Ведь скорость в физике — это часто встречающееся понятие, которое легко запомнить.
Цель : продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Задачи :
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел — скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.

Оборудование : карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
учебник.
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы : формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.
Учитель : Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам — шофер (Имитируют управление автомобильным рулем.)
И сам — мотор.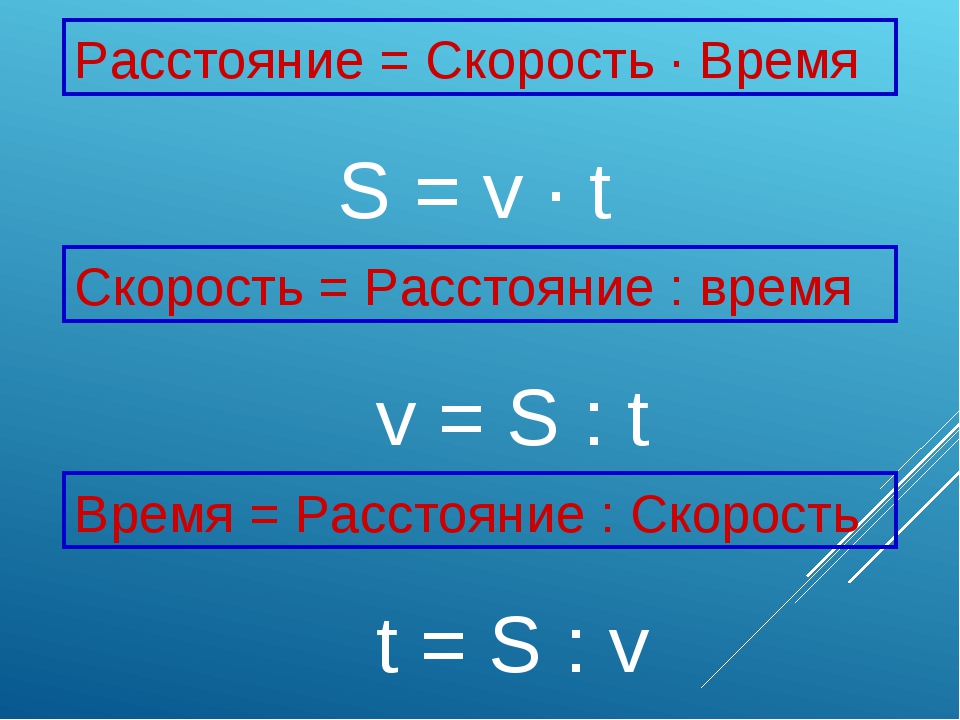
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Слайд № 6
Решение задачи № 2
Автобус
S — 90 км 90: 45= 2 часа
T — ?
V — 45 км/ч
Легковая машина
S — 270 км 270: 90 = 3 часа
T — ?
V — 90 км/ч
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный — радость
- Жёлтый — приятное
- Зелёный — спокойное
- Синий — грустное
- Фиолетовый — тревожный
- Оранжевый — удовлетворение
- Чёрный — неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок —
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Скорость является одной из основных характеристик . Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
Единицей измерения скорости в системе СИ является м/с .
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).
Отрицательная скорость
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
Равномерное и неравномерно движение
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.
ОПРЕДЕЛЕНИЕ
Равномерное движение – это движение с постоянной по модулю скоростью.
В случае неравномерного движения говорят о :
Примеры решения задач по теме «Скорость»
ПРИМЕР 1
| Задание | Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля. Определите среднюю скорость автомобиля. |
| Решение | Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. Воспользуемся определением средней скорости: Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить. Время, потраченное автомобилем на прохождение всего отрезка пути: где — время, затраченное на прохождение первой половины пути, а — время, затраченное на прохождение второй половины пути. Суммарное перемещение равно расстоянию между населенными пунктами, т.е. . Подставив эти соотношения в формулу для средней скорости, получим: Переведем скорости на отдельных участках в систему СИ: Тогда средняя скорость автомобиля: (м/с) |
| Ответ | Средняя скорость автомобиля равна 18,8 м/с |
ПРИМЕР 2
| Задание | Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля. Определить среднюю скорость автомобиля. |
| Решение | Сделаем рисунок. |
Как вы думаете, кто двигается быстрее агроном Васечкин, автомобиль Renault или самолет Боинг? Кто из них быстрее доберется от Москвы до Краснодара? Ответ очевиден Renault быстрее Васечкина, но медленнее Боинга.
То есть мы не только знаем, как двигаются разные объекты, но и можем сравнить их скорости. А что такое скорость в физике? Как найти скорость тела, и что такое единицы измерения скорости?
Скорость в физике: как найти скорость?
В 7 классе на уроках физики вводят понятие скорости. Без сомнения, все школьники к этому моменту уже знакомы с этим словом и представляют, что оно означает.
- А также знают, что скорость измеряется в км/ч и обозначается буквой V.
Но объяснить, что же такое скорость в физике, каковы единицы скорости, связно вряд ли смогут. Именно потому это простое, казалось бы, понятие требует пояснений и разбора.
В физике быстроту движения Васечкина, Renault и Боинга называют скоростью их движения. И скорость эта характеризует, какой путь преодолевает каждый из участников этого путешествия за единицу времени. И если в полете расстояние в 1350 километров между Москвой и Краснодаром мы преодолеем за два часа, на машине нам потребуется никак не меньше 15 часов, то пешком бесшабашный Васечкин сможет в бодром темпе как раз прошагать весь свой отпуск и прибыть на место лишь для того, чтобы поцеловать тещу, отведать блинов и сесть на самолет до Москвы, дабы успеть на работу в понедельник.
Соответственно, за единицу времени за час самолет пролетит 670 километров, машина проедет 90 километров, а турист Васечкин отмахает аж целых пять километров дороги. И тогда говорят, что скорость самолета 670 километров в час, машины 90 км в час, а пешехода 5 км/ч. То есть, скорость определяется делением пройденного пути на единицу времени на час, на минуту или на секунду.
Единицы измерения скорости
На практике применяются такие единицы, как км/ч, м/с и некоторые другие. Обозначают скорость буквой v, расстояние буквой s, а время буквой t. Формула для нахождения скорости в физике выглядит так:
Обозначают скорость буквой v, расстояние буквой s, а время буквой t. Формула для нахождения скорости в физике выглядит так:
Где s — пройденный путь
t — время, затраченное на преодоление этого пути
А если нам надо пересчитать скорость не в километрах в час, а в метрах за секунду, то пересчет происходит следующим образом. Так как 1 км=1000 м, а 1 ч = 60 мин = 3600 с, то можно записать: 1 км/ч=(1000 м)/(3600 с). И тогда скорость самолета будет равна: 670 км/ч=670×(1000 м)/(3600 с)=186м/с
Кроме своего числового значения, скорость имеет еще и направление, поэтому на рисунках скорость обозначают стрелкой и называют векторной величиной.
Средняя скорость в физике
Отметим еще один момент. В нашем примере водитель машины вел машину со скоростью 90 км/ч. По шоссе он мог ехать равномерно с такой скоростью долгое время. А вот проезжая по пути разные города, он то останавливался на светофорах, то полз в пробках, то короткими урывками набирал хорошую скорость.
Т.е. его скорость на разных участках пути была неравномерной. В таком случае вводят понятие средней скорости. Средняя скорость в физике обозначается V_ср и считается также как и скорость при равномерном движении. Только берут общее расстояние пути и делят на общее время.
Скорость численно равна пути (путь обозначается S), пройденного телом за единицу времени (время обозначается t).
Единица измерения скорость — это метр в секунду (м/с).
Скорость в физической науке обозначается латинской буквой «V».
Основной его расшифровкой служит определение: Скорость — это отношение пройденного пути (расстояния) за определенный промежуток времени. То есть: V=S/t
Основной единицей измерения скорости, как можно понять из формулы, служит отношение км/ч (иногда м/с). А вообще, данную единицу измерения скорости можно переформулировать в зависимости от процесса и науки, в котором ее измеряют!
Обычно в физике скорость обозначается латинской буквой v. Иногда эту букву пишут прописной, иногда строчной.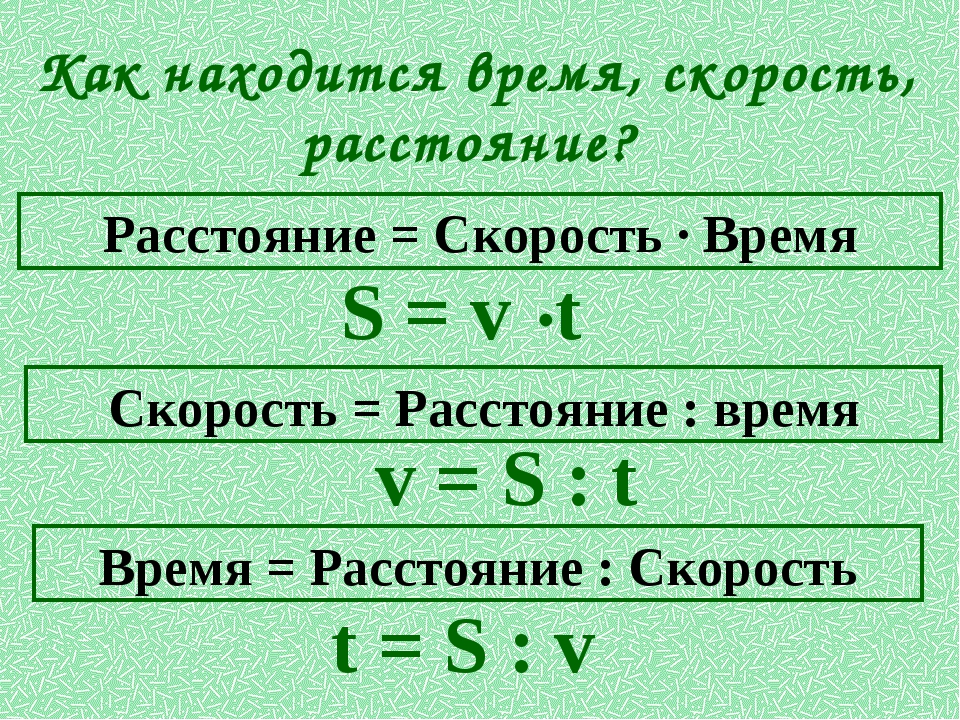
Однако есть одно исключение. Скорость обозначается буквой с, если равна скорости света.
111111 222222 333333 444444
Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Для того, чтобы отличить скорость света от переменной скорости, эти скорости обозначаются разными буквами.
Скорость в физике, алгебре и других науках принято обозначать латинской буквой v (английская буква в). Измеряется скорость по системе СИ в метрах в секунду — м/с. Скорость может являться векторной величиной, в алгебре и физике в таком случае над обозначающей скорость буквой ставится значок вектора.
Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета. Скорость обычно обозначается английской буквой «V». Как правило в физике и математике рассматривается скорость какого-либо тела.
В физике скорость обозначают латинской «V». Еще с уроков математики помню формулу:
Скорость равна: расстояние разделить на затраченное время.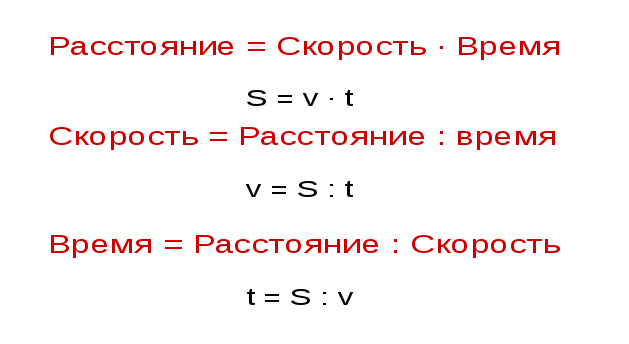
Бесплатная юридическая консультация:
Вот так выглядят эти формулы:
Измеряется скорость обычно в км/ч, хотя иногда измеряют в м/с.
Скорость в физики имеет символ от латинской буквы «V», только прописной и в некоторых случаях со стрелкой сверху, которая смотрит направо, к сожалению редактор не поддерживает прописную букву, поэтому приходится на картинке показать:
В физике, как впрочем и в математике, скорость обозначается латинской буквой «V».
Все мы прекрасно помним еще со школы, чтобы найти Скорость (V), нужно Расстояние (S) разделить на Время (t), которое затратили на преодоление этого расстояния (пути).
Бесплатная юридическая консультация:
Скорость движущихся объектов может измеряться в км/ч или м/с.
Насколько мне известно, в настоящее время в физике скорость обозначается буквой «V». Вообще, существует ещё скорость света, которая является постоянной величиной, и обозначается буквой «C». Кстати, скорость всегда равняется отношению пройденного расстояния в единицу времени.
Скорость обозначается буквой —
Скорость величина векторая, так что зачастую требуется указывать направление скорость.
Самая простая формула скорость, это длина деленная на расстояние.
Бесплатная юридическая консультация:
Очень часто люди путают скорость с ускорением, что приводит плохим последствиям.
Латинской буквой V. Такое обозначение используется и в математике, и в физике.
Список обозначений в физике
Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин. Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Бесплатная юридическая консультация:
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
В силу исторических причин, многие из обозначений используют латинские буквы — от первой буквы слова, обозначающего понятие на иностранном языке (преимущественно латинском, английском, французском и немецком). Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква O .
Среди латинских букв для обозначения физических величин практически не используется буква O .
Обозначения с несколькими буквами
Для обозначения некоторых величин иногда используют несколько букв или и отдельные слова или аббревиатуры. Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Латинские названия математических функций и операций, которые часто используются в физике:
Крупные греческие буквы, которые в написании похожи на латинские (A , B , E , Z , H , I , K , M , N , O , P , T , Υ , X ,\mathrm ,\mathrm ,\mathrm ,\mathrm ,\mathrm ,\mathrm ,\mathrm ,\mathrm
,\mathrm ,\Upsilon ,\mathrm >) используются очень редко.
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж . Гребень Дирака иногда обозначают буквой Ш , так как график функции визуально схож с формой буквы.
Гребень Дирака иногда обозначают буквой Ш , так как график функции визуально схож с формой буквы.
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Например, f(x, y) означает, что величина f является функцией x и y.
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x .
Обозначения физических величин часто имеют нижний, верхний, или оба индекса. Обычно нижний индекс обозначает характерный признак величины, например её порядковый номер, тип, проекцию и т. п. Верхний индекс обозначает степень, кроме случаев, когда величина является тензором.
Для наглядного обозначения физических процессов и математических операций используются графические обозначения: Фейнмановские диаграммы, спиновые сети и графические обозначения Пенроуза.
обозначение скорости
2.33 обозначение скорости:
2.33. 1. Буква алфавита, указывающая скорость, на которой шина может использоваться при нагрузке, о которой свидетельствует соответствующий индекс нагрузки;
1. Буква алфавита, указывающая скорость, на которой шина может использоваться при нагрузке, о которой свидетельствует соответствующий индекс нагрузки;
2.33.2. Обозначения скорости и соответствующие им максимальные значения приведены в таблице 2.
Словарь-справочник терминов нормативно-технической документации. academic.ru . 2015 .
Смотреть что такое «обозначение скорости» в других словарях:
Обозначение — сопряжения, контролируемого размера, поверхности или зоны контроля, номер сварного шва или обозначение пересечения сварных швов, указываемого номерами сварных швов, через тире, например № 1 2, и других параметров. Источник … Словарь-справочник терминов нормативно-технической документации
коэффициент скорости реактивного сопла — коэффициент скорости сопла Отношение средней по массе скорости газа в выходном сечении реактивного сопла ГТД к идеальной скорости, соответствующей расширению потока газа до давления в окружающей среде. Обозначение φс [ГОСТ] Тематики… … Справочник технического переводчика
ГОСТ Р7: Инструмент абразивный.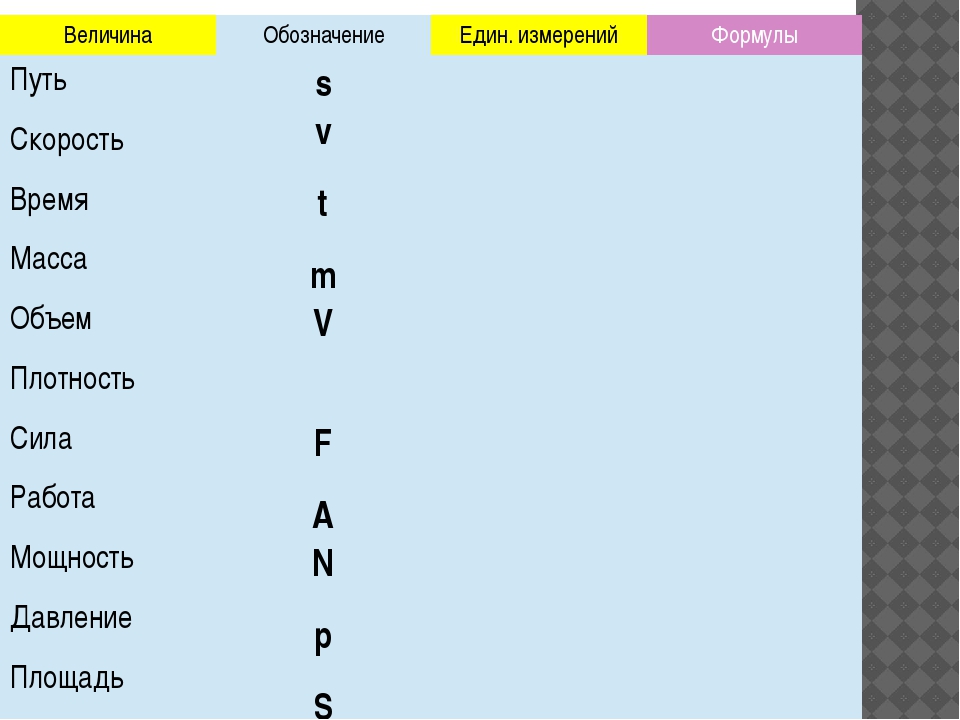 Акустический метод определения твердости и звуковых индексов по скорости распространения акустических волн — Терминология ГОСТ Р7: Инструмент абразивный. Акустический метод определения твердости и звуковых индексов по скорости распространения акустических волн оригинал документа: 3.2 звуковой индекс абразивного инструмента; ЗИ: Условное… … Словарь-справочник терминов нормативно-технической документации
Акустический метод определения твердости и звуковых индексов по скорости распространения акустических волн — Терминология ГОСТ Р7: Инструмент абразивный. Акустический метод определения твердости и звуковых индексов по скорости распространения акустических волн оригинал документа: 3.2 звуковой индекс абразивного инструмента; ЗИ: Условное… … Словарь-справочник терминов нормативно-технической документации
категория скорости пневматической шины — категория скорости шины Условное обозначение, определяющее максимальную скорость качения пневматической шины. [ГОСТ] Тематики шины пневматические Обобщающие термины конструктивные обозначения пневматических шин Синонимы категория… … Справочник технического переводчика
категория скорости массивной шины — Условное обозначение, определяющее максимальную скорость качения массивной шины. [ГОСТ] Тематики шины пневматические Обобщающие термины показатели функциональной и технической эффективности массивных шин EN speed category FR catégorié de … Справочник технического переводчика
ГОСТ Р 41. 109-99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов — Терминология ГОСТ Р 41.109 99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов оригинал документа: 2.38 … Словарь-справочник терминов нормативно-технической документации
109-99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов — Терминология ГОСТ Р 41.109 99: Единообразные предписания, касающиеся официального утверждения в отношении производства шин с восстановленным протектором для транспортных средств неиндивидуального пользования и их прицепов оригинал документа: 2.38 … Словарь-справочник терминов нормативно-технической документации
Индекс — 6. Индекс Кодированная импульсная последовательность, записанная на сервоповерхности вида: dddddododdo, где d означает: для сервозоны пару дибитов, для защитных зон одиночный дибит; о означает: для сервозоны отсутствующую пару дибитов, для… … Словарь-справочник терминов нормативно-технической документации
индекс нагрузки — 2.32 индекс нагрузки: Цифровая кодировка, свидетельствующая о нагрузке, которую может выдержать шина при скорости, на которую указывает соответствующее обозначение скорости, и в рабочем режиме, соответствующем условиям эксплуатации, указанным… … Словарь-справочник терминов нормативно-технической документации
Трель — Обозначение трели Трель (итал. trillare дребезжать) один из наиболее употребительных мелизмов; быстрое чередование двух соседних нот, отстоящих на секунду, большую или малую. Первая нота называется главной и по отношению к… … Википедия
trillare дребезжать) один из наиболее употребительных мелизмов; быстрое чередование двух соседних нот, отстоящих на секунду, большую или малую. Первая нота называется главной и по отношению к… … Википедия
Симистор — Обозначение на схемах Эквивалентная схема симистора … Википедия
Книги
- Угол атаки, Джесси Рассел. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. High Quality Content by WIKIPEDIA articles! Угол атаки (общепринятое обозначение — буква… ПодробнееКупить за 743 руб
Мы используем куки для наилучшего представления нашего сайта. Продолжая использовать данный сайт, вы соглашаетесь с этим. Хорошо
Как обозначается скорость
Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел — скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.

- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование: карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы: формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Ход урока
Организационный момент
Прозвенел заливистый школьный звонок.
Учитель: Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Извычти частное числои 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисели 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
(образец в тетради)
Прочитайте числа.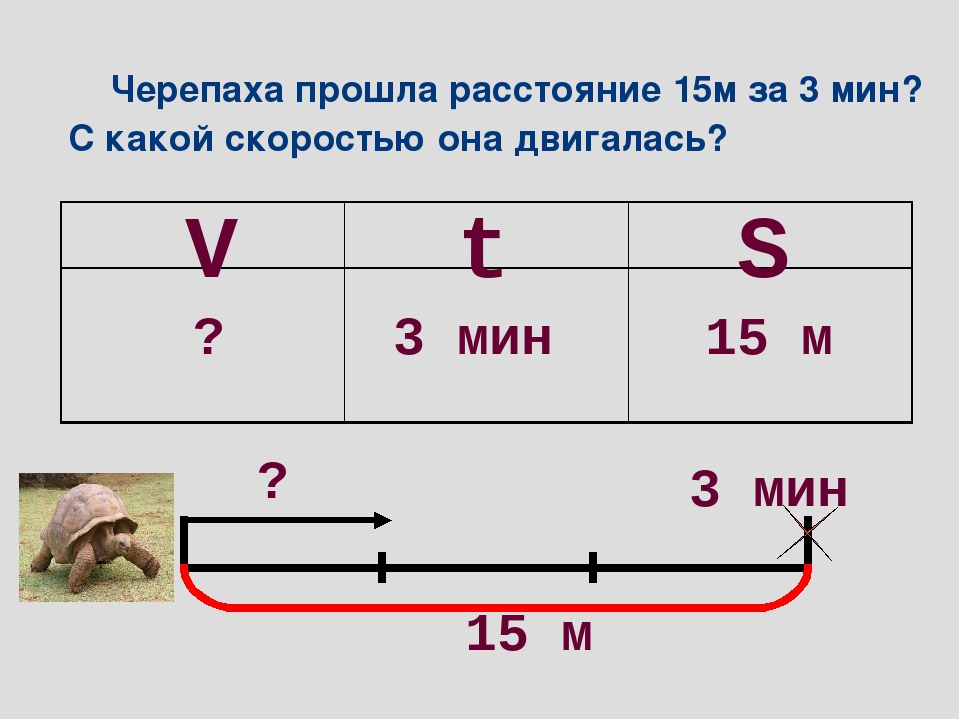 Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Физминутка
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам — шофер (Имитируют управление автомобильным рулем.)
И сам — мотор. (Круговые движения плечами вперед-назад. )
)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Решение задачи № 2
S — 90 км 90: 45= 2 часа
Sкм 270: 90 = 3 часа
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный — радость
- Жёлтый — приятное
- Зелёный — спокойное
- Синий — грустное
- Фиолетовый — тревожный
- Оранжевый — удовлетворение
- Чёрный — неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок —
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен58 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Как известно, масса тела равна его объему, умноженному на плотность. Обычно это утверждение записывается в виде формулы, посредством общепринятых условных обозначений.
Как обозначается объём
И в математике, и в физике объём обозначается буквой V. Произносится это обозначение так же, как и обозначение скорости, т.е. [вэ], но визуально обозначения различны. Скорость обозначается строчной (т.е. маленькой) буквой v, а объём обозначается заглавной (т.е. большой) буквой V.
Произносится это обозначение так же, как и обозначение скорости, т.е. [вэ], но визуально обозначения различны. Скорость обозначается строчной (т.е. маленькой) буквой v, а объём обозначается заглавной (т.е. большой) буквой V.
Как обозначается плотность
Плотность обозначается греческой буквой «ро». Этой буквой обозначается плотность любого вещества (газа, воды или любой другой жидкости, воздуха, металла, льда и прочего). При необходимости, если требуется в рамках одной задачи обозначить плотность нескольких веществ, используются нижние индексы (буквенные, числовые или буквенно-числовые). Поскольку буквенные индексы имеют преимущество — смысловой оттенок, их использование предпочтительнее, чем числовых. Например, плотность льда можно обозначить как р л, а плотность воды — как р в. Такие обозначения, со смысловым оттенком, удобнее, чем р 1 и р 2 . Но, если необходимо обозначить, к примеру, плотность нескольких жидкостей, будут удобны числовые индексы: р 1, р 2 , р 3 , р 4 , р 5 . Если нужно обозначить плотности нескольких жидкостей и нескольких газов, целесообразно использовать буквенно-числовые индексы: р ж1, р ж2 , р ж3 , р ж4 , р ж5 для жидкостей и р г1, р г2 , р г3 , р г4 , р г5 для газов.
Если нужно обозначить плотности нескольких жидкостей и нескольких газов, целесообразно использовать буквенно-числовые индексы: р ж1, р ж2 , р ж3 , р ж4 , р ж5 для жидкостей и р г1, р г2 , р г3 , р г4 , р г5 для газов.
Как обозначается масса тела
Масса тела обозначается буквой «m» (читается: [эм]). При необходимости, в обозначении массы используются нижние буквенные, числовые или буквенно-числовые символы. Например, массу шара и массу куба можно обозначить в одной задаче как m ш m к (в данном случае буквенные индексы использовать удобнее, так как они несут смысловую нагрузку). Если же нужно обозначить массы, например, десяти коробок, то удобнее пользоваться числовыми индексами (m 1 , m 2 , m 3 и т.д.)
Как обозначается вес тела
В физике часто приходится обозначать буквой вес тела. Для этого используют буквы G (читается: [жэ]) или Р (читается: [пэ]). Когда речь идёт о собственном весе тела, обычно используют букву G. Когда речь идёт о весе тел, создающих внешнюю нагрузку на рассматриваемое тело, их вес обозначается обычно буквой Р, но может использоваться и G.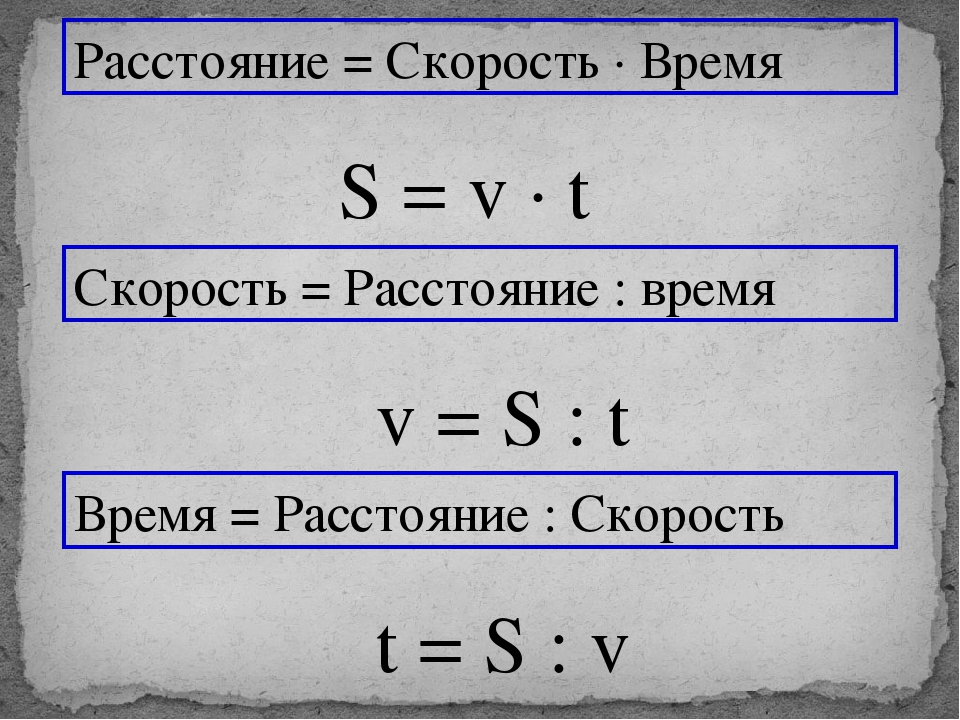 При необходимости, к этим обозначениям добавляют нижний индекс (числовой, буквенный или буквенно-числовой). Например, рассматривается балка массой m. Её собственный вес G = m*g. На этой балке расположены грузы массой m 1 , m 2 , m 3 , m 4 , m 5 . По отношению к этой балке они создают внешнюю нагрузку, поэтому их вес обычно обозначается не буквой G, а буквой Р (Р 1 , Р 2 , Р 3 , Р 4 , Р 5). Если же речь шла бы не о балке, а непосредственно об этих пяти грузах, для обозначения их веса была бы выбрана буква G (т.е. G 1 , G 2 , G 3 , G 4 , G 5). Бывает, что при обозначении веса удобно использовать не числовые, а буквенные или буквенно-числовые индексы. Например, если в одной задаче нужно обозначить вес шара и вес цилиндра, в качестве индекса лучше использовать не «1» и «2», а несущие смысловой оттенок «ш» и «ц». Если же в одной задаче нужно обозначить, например, вес двух шаров и трех цилиндров, лучше использовать буквенно-числовые нижние индексы: G ш1 , G ш2 , G ц1 , G ц2 , G ц3 .
При необходимости, к этим обозначениям добавляют нижний индекс (числовой, буквенный или буквенно-числовой). Например, рассматривается балка массой m. Её собственный вес G = m*g. На этой балке расположены грузы массой m 1 , m 2 , m 3 , m 4 , m 5 . По отношению к этой балке они создают внешнюю нагрузку, поэтому их вес обычно обозначается не буквой G, а буквой Р (Р 1 , Р 2 , Р 3 , Р 4 , Р 5). Если же речь шла бы не о балке, а непосредственно об этих пяти грузах, для обозначения их веса была бы выбрана буква G (т.е. G 1 , G 2 , G 3 , G 4 , G 5). Бывает, что при обозначении веса удобно использовать не числовые, а буквенные или буквенно-числовые индексы. Например, если в одной задаче нужно обозначить вес шара и вес цилиндра, в качестве индекса лучше использовать не «1» и «2», а несущие смысловой оттенок «ш» и «ц». Если же в одной задаче нужно обозначить, например, вес двух шаров и трех цилиндров, лучше использовать буквенно-числовые нижние индексы: G ш1 , G ш2 , G ц1 , G ц2 , G ц3 .
Читайте также.
Как устроиться на работу в полицию
Как научиться делать шпагат — хорошая растяжка без возрастных ограничений
Как самому изготовить защитную сетку от насекомых — видео
Как послушнику в монастыре живется
Работа со сводными таблицами в экселе
Как сделать морфологический разбор
Выбираем самые модные и актуальные платья
Вполне может быть, что за этим также скрывается какая-нибудь серьёзная легенда о том, что данный амулет будет защищать вас «до гроба», а то и дольше
Делаем короб для сабвуфера своими руками
Карта скидок. Что она даёт? Как получить? Нужна ли от «Икеа Фэмили» карта? Как получить, и что она дает?
Как научиться рисовать: советы для начинающих
Большая Энциклопедия Нефти и Газа
Обозначение — скорость
Обозначения скоростей и углов см. фиг.
Припишем обозначениям скорости и эффективной массы отсутствующих электронов индекс О и определим отсутствующий электрон (или дырку) как гипотетическую частицу, представляющую собой совокупность электронов заполненной зоны, в которой отсутствует только один электрон.
Индекс 1 принят для обозначения скоростей и углов на входе в рабочее колесо, индекс 2 — на выходе из него.
Индекс 1 принят для обозначения скоростей жидкости на входе в рабочее колесо, индекс 2 — на выходе из него.
Введем также индекс 1 для обозначения скоростей и углов на входе в рабочее колесо и индекс 2 — на выходе из него.
Введем также индекс 1 для обозначения скоростей и углов на входе в рабочее колесо и индекс 2 для обозначения тех же величин на выходе из него.
XII-XIV мы используем U для обозначения скорости свободного потока вместо (обычно не существующего) потенциала скорости.
Около ручек управления на шильдиках нанесены обозначения скорости вращения диска, включения и выключения ЭПУ, включенного и выключенного положения автостопа.
Около ручек управления на шильдиках нанесены обозначения скоростей вращения диска, включения и выключения ЭПУ, включенного и выключенного положения автостопа.
Дорожки 2, 8 и 4 служат для обозначения скорости вращения шпинделя, при которой выполняется данный этап технологического цикла.
Урок математики в 3-м классе по теме «Скорость. Время. Расстояние»
Цели урока:
- ввести понятие скорости как новой единицы измерения; установить зависимости между величинами – скорость, время, расстояние; учить решать задачи на нахождение скорости по известным расстоянию и времени движения используя формулу движения;
- повторить табличные и внетабличные случаи умножения и деления, формировать вычислительные навыки, закрепить знание единиц времени и длины;
- способствовать развитию логического мышления, внимания, речи, самостоятельности;
- прививать интерес к физкультуре и спорту.
Планируемые достижения учащихся на уроке:
- знать понятие скорости как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание
единиц длины и времени.

Оборудование: Петерсон Л.Г. Математика, 3кл., III часть; рабочая тетрадь по математике, сигнальные карты, таблицы с дифференцированными заданиями для самостоятельной работы, название единиц длины и единиц времени на карточках, индивидуальные карточки для учащихся, нарисованные герои “Улицы Сезам” (Зелибоба, Кубик, Бусинка).
ХОД УРОКА
- Самоопределение к деятельности.
Урок я хочу начать словами французского философа Ж.Ж. Руссо (1712-1778гг.): “Вы — талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” Я желаю вам уже сегодня на уроке убедиться в этих словах, ведь вас ждёт открытие новых знаний при решении задач.
- Актуализация знаний.
- Узнав о том, что вы любите смотреть детские телепрограммы, я пригласила
героев одной телепередачи к нам на урок.
 А они появятся здесь, как только вы
назовёте эту передачу. Но слова зашифрованы. Что же делать?
А они появятся здесь, как только вы
назовёте эту передачу. Но слова зашифрованы. Что же делать? - Правильно, надо решить примеры и расшифровать слова. Для этого вам необходимо вспомнить табличные и внетабличные случаи умножения и деления.
- Приготовьте сигнальные карты, контролируем правильность решения примеров.
(Два ученика работают индивидуально на карточках.)
|
|
Индивидуальные задания на карточках
|
|
- Почему некоторые ребята допускали ошибки? Как этого избежать?
- Что мы им посоветуем?
- Прочитайте слова, расставляя ответы в порядке убывания.

I вариант – первое слово (1 столбик)
II вариант – второе слово (2 столбик)
- Кто готов? (Улица, Сезам)
- Молодцы, ваши знания помогли вам расшифровать названия передачи. У нас в гостях “Улица Сезам”.
- Назовите героев этой передачи. (Зелибоба, Бусинка и Кубик)
- Наши друзья ведут здоровый образ жизни, учатся правильно питаться, занимаются спортом. Увлекаясь ходьбой на лыжах, Зелибоба и Кубик решили всерьёз заняться лыжным спортом и готовиться к Зимним Олимпийским играм, которые пройдут в г. Сочи в 2014 году.
Бусинка объявила старт. Соперники преодолели путь 24 метра. Зелибоба пришёл к финишу через 3 минуты, а Кубик через 4 минуты.
Проблемный вопрос: Почему так произошло? (Один быстрее двигался, а другой медленнее)
- Да, они двигались с разной скоростью.
- Где вы встречались с понятием “скорость”? (В машине спидометр измеряет скорость)
- Как измерить скорость движущихся тел, у которых нет спидометра?
- Назовите тему урока.

- Что будем учиться измерять на уроке?
- Постановка темы урока
- Чтобы точнее сформулировать тему и цели урока, найдём опорные слова. Они необходимы для определения скорости. Для этого, работая в парах, расположите данные вас единицы измерения в порядке возрастания.
- Какие единицы измерения у I и III ряда? (Длины)
- У II ряда? (Времени)
Кто готов назвать их в порядке возрастания? (Ученики называют и выкладывают на наборное полотно.)
мм, см, дм, м, км
с, мин, ч, сут, мес
Проверьте правильность выполнения, переверните каждую карточку и прочитайте слово. (I и III ряды: расстояние; II ряд: время)
Расстояние – это промежуток между двумя пунктами, точками, между
чем-нибудь. В чём измеряется расстояние? (В единицах длины).
Время – это продолжительность, длительность чего-нибудь.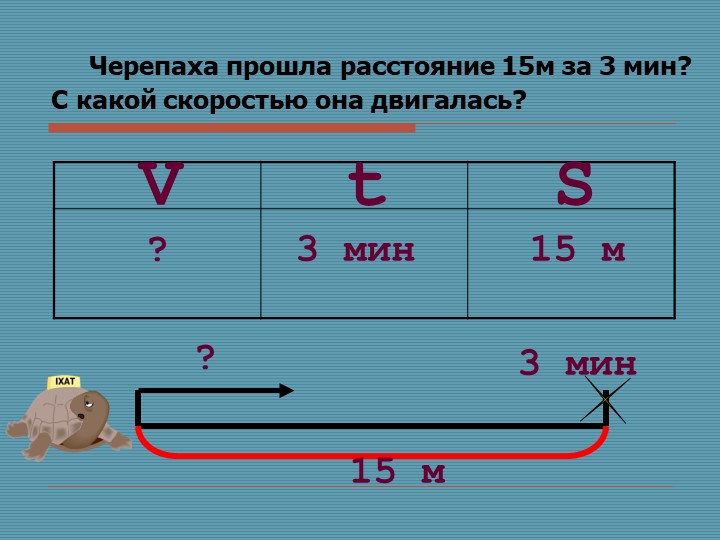 В чём измеряется время?
(В единицах времени).
В чём измеряется время?
(В единицах времени).
Проблемный вопрос:
- А что называется скоростью?
- В чём измеряется скорость движения?
- Уточните тему нашего урока. (Скорость. Время. Расстояние.)
- Чему будем учиться на уроке? (Ответы детей).
Сегодня нам предстоит узнать как скорость движения связана со временем движения и расстоянием, научиться решать задачи на нахождение скорости движения.
- Открытие новых знаний.
- Что называют скоростью? Где найти ответ на наш вопрос? (В учебнике)
- Откройте учебник с. 1, найдите выделенное слово “скоростью”. Прочитаем определение скорости. (Скоростью называют расстояние, пройденное в единицу времени.)
- Так что же называют скоростью?
- Какими величинами будем пользоваться для определения скорости? (Расстоянием и временем)
- И в качестве единиц измерения скорости мы будем пользоваться и единицами
длины и единицами времени.

- Обычно используют такие единицы скорости, как метр в секунду, метр в минуту, километр в час, а записывают так: м/с, м/мин, км/ч. Обратите внимание, что предлог “в” в математике заменили чёрточкой “ / ”.
- Прочитайте единицы скорости км/с м/мин км/ч м/с
- Из каких единиц измерения образуются названия единиц скорости? (Из единиц длины и единиц времени).
Физминутка.
Руки ставим все вразлёт,
Появился самолёт.
Мах крылом туда-сюда,
Делай раз и делай два.
Отпустите руки вниз
И на место все садитесь.
Работа с учебником
- Интересно, а какая скорость у самолёта?
- Объясните смысл предложений, записанных в задании № 1, стр.2. (Самолёт летит со скоростью 800 км/ч, т.е. за 1 ч самолёт преодолевает расстояние 800 км)
Молодцы. Откройте тетради, запишите число, классная работа. Следите за
осанкой. Мы будем учиться решать задачи на нахождение скорости движения по данному
расстоянию и времени. Зелибоба и Кубик очень хотят узнать свою скорость движения. Поможем им. Решим
задачу.
Откройте тетради, запишите число, классная работа. Следите за
осанкой. Мы будем учиться решать задачи на нахождение скорости движения по данному
расстоянию и времени. Зелибоба и Кубик очень хотят узнать свою скорость движения. Поможем им. Решим
задачу.
Задача 1. Зелибоба прошёл на лыжах расстояние, равное 24 метрам за 3 минуты. С какой скоростью он шёл?
Что нам известно?
- Расстояние – 24 м
- Время – 3 мин.
Что нужно узнать? Скорость Зелибобы, т.е. расстояние, которое проходил Зелибоба за 1 мин.
Сделаем чертёж к задаче
Чертим отрезок. Чему равно расстояние? Обозначим время на отрезке. Весь путь, который прошёл Зелибоба, мы может разделить на 3 равные части, потому что в каждую минуту Зелибоба проходил одинаковое расстояние.
- Кто из вас догадался, с какой скоростью двигался Зелибоба?
- Как узнать скорость его движения? (Расстояние разделить на время)
Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы.
Т.е. за 1 мин Зелибоба проходил 8 м.
Напишем ответ задачи. Ответ: 8 м/мин.
- Первичное закрепление.
Закрепим умение решать задачи на движение, а именно на нахождение скорости.
Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. С какой скоростью двигался Кубик?
- Что известно в задаче? (Расстояние – 24 м, время – 4 минуты)
- Что надо узнать? (Скорость Кубика)
На доске чертёж.
Ребята, а всегда ли удобно делать чертёж к задаче? В Математике принято обозначать величины латинскими буквами:
- расстояние – S
- время – t
- скорость — v
Итак, запишем в тетрадь:
- Как найти скорость движения? (Расстояние разделить на время)
- Скажите мне то же самое, только при помощи буквенных обозначений: v = S ׃ t
Вы назвали формулу, по которой находят скорость движения. Этой формулой вы
будете пользоваться и в старших классах. Запишем решение задачи. (Ученик у доски).
Этой формулой вы
будете пользоваться и в старших классах. Запишем решение задачи. (Ученик у доски).
v = S ׃ t
24 ׃ 4 = 6 (м/мин) скорость Кубика.
Ответ: 6 м/мин.
Сравните скорость Зелибобы и Кубика. Почему Зелибоба пришёл к финишу раньше?
Вывод: Скорость – это величина, которую можно измерить и сравнить.
Зелибоба и Кубик довольны. Вместе с вами они научились измерять скорость движения.
- Самостоятельная работа.
Давайте потренируемся в решении задач на нахождение скорости, выполняя работу самостоятельно.
Бусинка вам предлагает найти скорость движения своих друзей в других видах спорта. Заполните таблицы, записывая только ответы. (Задание дифференцированные по сложности и обьему.)
Как будете находить скорость движения? Будьте внимательны при обозначении скорости.
1 группа
| Движущиеся тела | Расстояние, S м | Время, t, мин | Скорость, v м/мин |
| Конькобежец | 80 м | 2 мин | |
| Пловец | 45 м | 5 мин |
2 группа
| Движущиеся тела | Расстояние, S м | Время, t, мин | Скорость, v м/мин |
| Конькобежец | 80 м | 2 мин | |
| Пловец | 45 м | 5 мин | |
| Велосипедист | 480 м | 4 мин |
Проверьте свои ответы с ответами Бусинки. Приложение 1
Приложение 1
- Кто выполнил работу без ошибок? – Молодцы, поставьте себе 5.
- Кто допустил 1 ошибку? – Поставьте себе 4. – Бусинка вами довольна.
- Кто допусти 2 ошибки? Кто не справился? – Не огорчайтесь, потренируйтесь дома, приложите старание, тогда и у вас всё получится.
А наши друзья вам советуют заниматься спортом. Скажите, зачем нужно заниматься спортом? (Ответ детей). Правильно, спорт – это здоровье, сила, выносливость.
- Повторение с включением новых знаний.
Зелибоба приготовил вам игру. Нужны 3 ученика – это движущиеся модели: самолёт, машина, ракета. Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения?
(Самолёт – 800 км/ч; ракета – 6 км/с; машина – 90км/ч).
Молодцы.
- Кто из них движется быстрее всех?
- У кого самая маленькая скорость движения?
- На каком виде транспорта наши друзья меньше затратят времени на дорогу до Москвы?
А о том, как находить время движения вы узнаете на следующем уроке.
- Итог урока. Рефлексия деятельности.
Наш урок подходит к концу. Чему учились на уроке?
- Назовите формулу, которой будем пользоваться для определения скорости движения?
- Где сможете применить новые знания?
Время передачи “Улицы Сезам” истекает. Давайте “зажжём” фонарики на “Улице Сезам”.
- Кто доволен своей работой на уроке, понял новую тему – “зажгите” красный фонарик.
- Кто не совсем доволен, допускал ошибки – жёлтый.
- Кто не доволен своей работой – “зажжёт” синий.
Ваши фонарики мне говорят о том, что сегодня вы достигли успеха на уроке.
Интересно, а как вашу работу оценят наши друзья? (На “Улице Сезам” “зажигается” красный фонарик.) Как видите, наши друзья из передачи “Улица Сезам” довольны вашей работой на уроке.
- Домашнее задание.
Домашнее задание будет таким: решить задачи, определить скорости движущихся
тел — № 2, стр. 2, или придумать свою задачу, в которой надо найти скорость по
известному расстоянию и времени, и решить её — № 8, стр. 3.
2, или придумать свою задачу, в которой надо найти скорость по
известному расстоянию и времени, и решить её — № 8, стр. 3.
Благодарю за урок.
Чтобы найти t. Чтобы найти время, надо расстояние разделить на скорость. Как найти время, зная скорость и расстояние
Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
Люди, животные или машины могут двигаться с определенной скоростью. За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса. Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S . Скорость обозначается буквой v . А время, за которое пройден путь, обозначается буквой t .
- Путь — S
- Скорость — v
- Время — t
Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость.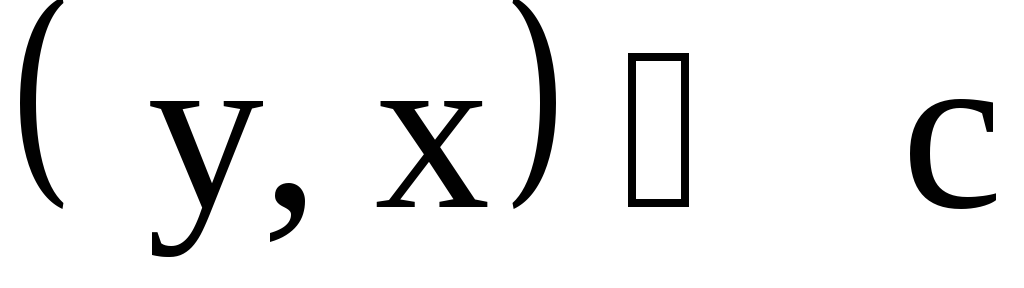 А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
Как зависит время прохождения пути от скорости?
Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.
Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Задача про Зайца. Заяц убегал от Волка со скоростью 1 километр за минуту. Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?
Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
- Внимательно прочитайте задачу и определите, что известно из условия задачи.
- Напишите на черновике эти данные.
- Также напишите, что неизвестно и что нужно найти
- Воспользуйтесь формулой для задач про расстояние, время и скорость
- Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
- Из условия задачи определяем, что нам известно скорость и расстояние.
- Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.
Пишем в черновик эти данные например так:
Время — неизвестно
Теперь запишем то же самое математическими знаками:
S — 3 километра
V — 1 км/мин
t — ?
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
t = S: v
t = 3: 1 = 3 минуты
Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?
Решение задачи на движение:
- В черновик записываем, что нам известно расстояние и время.

- Из условия задачи определяем, что нужно найти скорость
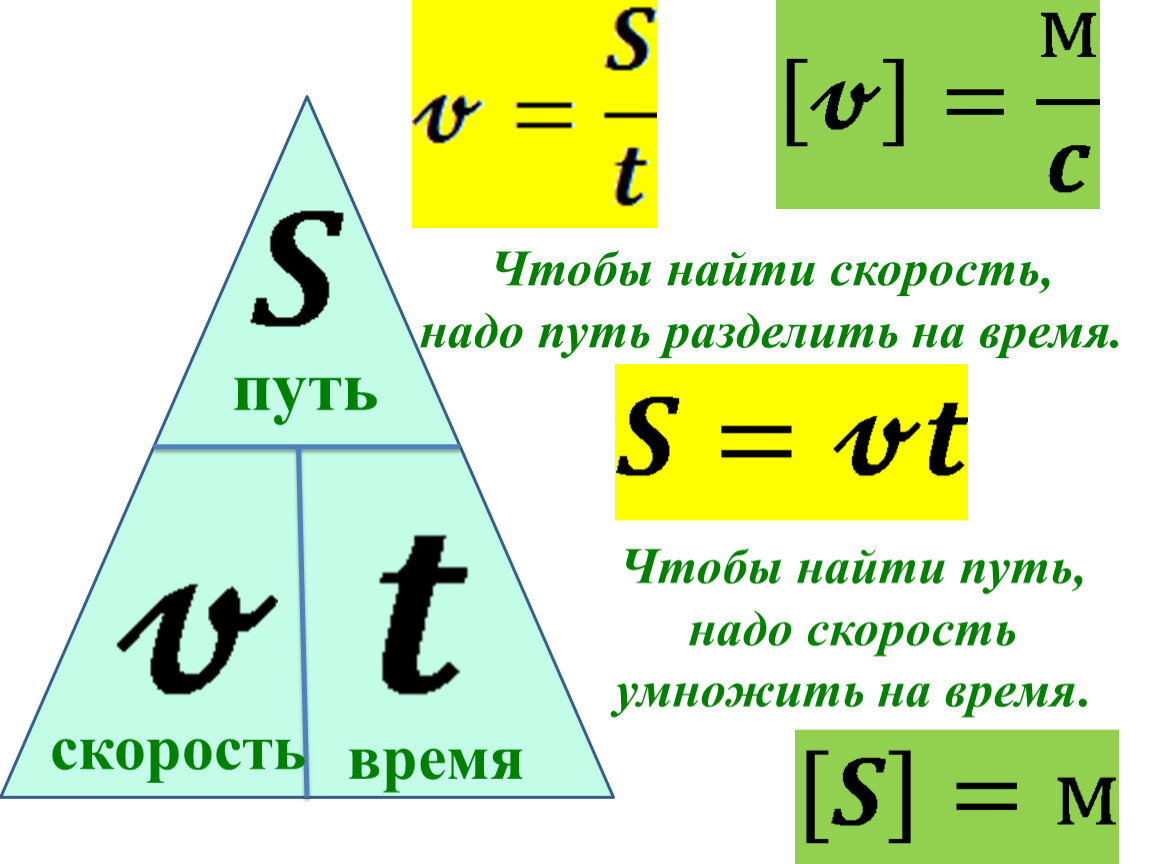
- Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.
Формулы для решения задач про расстояние, время и скорость
Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Скорость — неизвестна
Запишем эти известные данные математическими знаками
S — 3 километра
t — 3 минуты
v — ?
Записываем формулу для нахождения скорости
v = S: t
Теперь запишем решение задачи цифрами:
v = 3: 3 = 1 км/мин
Как найти расстояние, если известно время и скорость?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:
Заяц убегал от Волка со скоростью 1 километр за 1 минуту.
Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Решение задачи: Записываем в черновик, что нам известно из условия задачи:
Скорость Зайца — 1 километр за 1 минуту
Время, которое Заяц бежал до норы — 3 минуты
Расстояние — неизвестно
Теперь, то же самое запишем математическими знаками:
v — 1 км/мин
t — 3 минуты
S — ?
Вспоминаем формулу для нахождения расстояния:
S = v ⋅ t
Теперь запишем решение задачи цифрами:
S = 3 ⋅ 1 = 3 км
Как научиться решать более сложные задачи?
Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.
Ребенок, который умеет решать задачи, может гордиться собой
Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.
ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.
Для любознательных : Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.
Задача про удава : Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)
Решение:
Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.
Запишем эти данные:
Скорость мартышки — 60 см/сек
Скорость слоненка — 20 см/сек
Время — 5 секунд
Расстояние неизвестно
Запишем эти данные математическими знаками:
v1 — 60 см/сек
v2 — 20 см/сек
t — 5 секунд
S — ?
Запишем формулу для расстояние, если известна скорость и время:
S = v ⋅ t
Посчитаем, какое расстояние прошла мартышка:
S1 = 60 ⋅ 5 = 300 см
Теперь посчитаем, сколько прошел слоненок:
S2 = 20 ⋅ 5 = 100 см
Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:
S = S1 + S2 = 300 + 100 = 400 см
График зависимости скорости тела от времени: фото
Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
- Папа Ксюши купил автомобиль и решил отвезти семью на море.
 Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем? - Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?
Ответы на приведенные задачи можно найти в таблице ниже:
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примеры решения задач на скорость, время, расстояние за 4 класс
Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:
Пример такой задачи:
Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?
Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
S = v ⋅ t
Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
S = 10 ⋅ 1 = 10 километров
Расстояние, которое прошел Тема считают аналогично:
S = v ⋅ t
Подставляем в формулу цифровые значения его скорости и времени
S = 5 ⋅ 1 = 5 километров
Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
10 + 5 = 15 километров
Как научиться решать сложные задачи, для решения которых требуется логически мыслить?
Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи.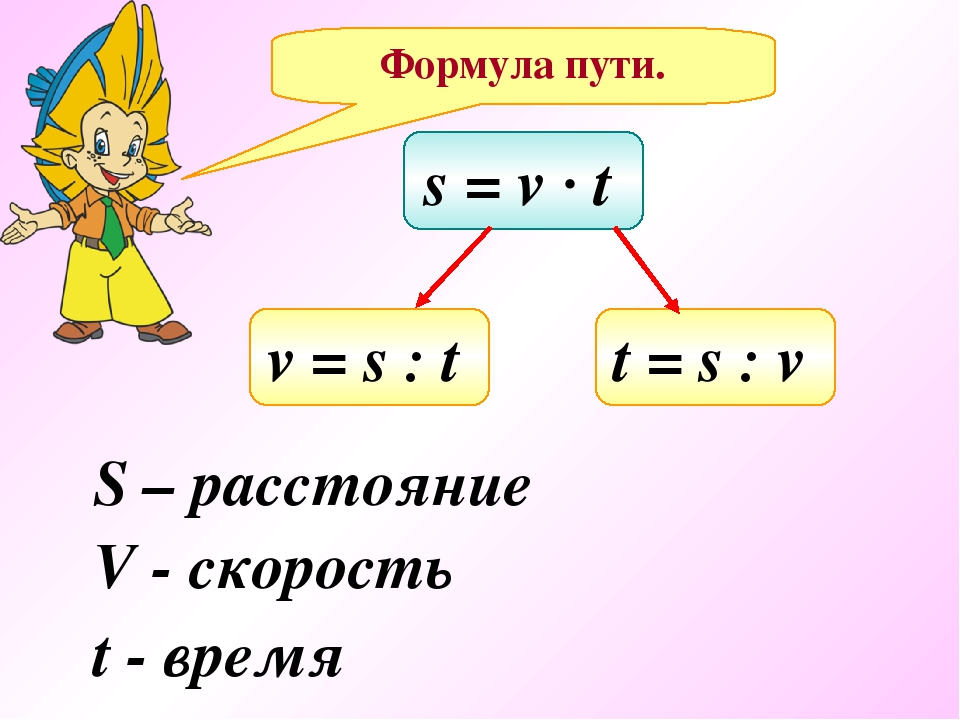 Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?
Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.
Кто едет быстрее? Задача про друзей
Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:
Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)
Решение:
- 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
- 60 : 20 = 3 (часа) — это время через которое велосипедисты встретились
- 3 ⋅ 8 = 24 (км) — это расстояние, которое проехал первый велосипедист
- 12 ⋅ 3 = 36 (км) — это расстояние, которое проехал второй велосипедист
- Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.

- Ответ: 24 км, 36 км.
Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.
ВИДЕО: Задачи на движение
Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.
Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.
Как найти скорость – равномерное движение
Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.
В первом случае траекторией перемещения тела является прямая.
Тогда V=S/t, где:
- V – искомая скорость,
- S – пройденное расстояние (общий путь),
- t – общее время движения.
Как найти скорость – ускорение постоянно
Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:
V=V (нач) + at, где:
- V (нач) – первоначальная скорость движения объекта,
- a – ускорение тела,
- t – общее время пути.
Как найти скорость – неравномерное движение
В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.
На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.
Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:
Как найти скорость – вращение объекта
В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени.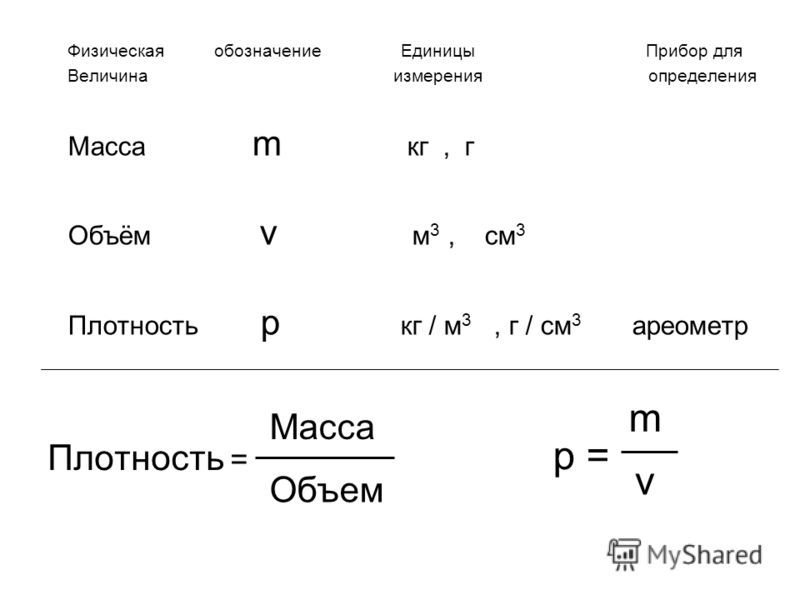 Обозначается искомая величина символом ω (рад/с).
Обозначается искомая величина символом ω (рад/с).
Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).
- В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:
ω = 2π/T, где:
π – константа ≈3,14,
T – период.
Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.
- При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:
ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.
Как найти скорость – сближение и отдаление точек
В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.
Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.
Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).
Как найти скорость – движение по водоему
Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?
В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).
Понятие времени (также как расстояние и скорость) — величина физическая. Оно характеризует промежуток, в течение которого объект изменяет свои свойства и используется в физике, и математике для решения задач на движение.
В качестве примера попробуем найти время, если известно расстояние и скорость, а также рассмотрим обратные способы расчёта неизвестных величин.
Быстрая навигация по статье
Определяем время
Для определения времени обычно пользуются распространённой формулой: t=S/v, где t- это время, S — расстояние, а v — скорость.
Таким образом, с помощью простых математических действий можно вычислить любую из этих величин, зная две другие. В данном случае у нас имеются значения скорости и расстояния. Чтобы узнать время, мы расстояние делим на скорость.
Эта же формула поможет вычислить скорость при условии, когда известны расстояние и время. Для этого выполняем простейшие математические действия с обыкновенными дробями.
Определяем скорость
Из формулы, по которой мы рассчитывали время, вычислим скорость. Это величина, равная расстоянию, пройденному за единицу времени.
Чтобы найти значение скорости, нужно поместить её с одной стороны знака равенства, а другие значения — с другой. Для вычисления знаменателя в этом уравнении, нужно числитель разделить на значение, находящееся с другой стороны знака равенства.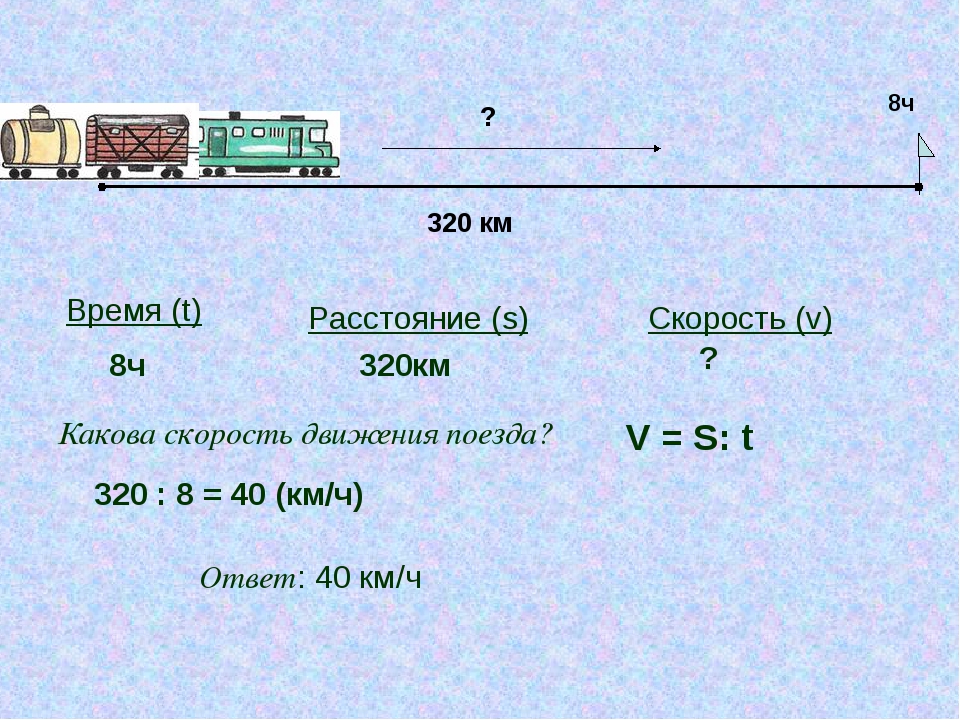 То есть, расстояние делим на время и получается следующая формула: v=S/t
То есть, расстояние делим на время и получается следующая формула: v=S/t
Определяем расстояние
По аналогии рассчитываем и расстояние. Оно будет определяться произведением времени на скорость: S=v*t
t = S: V
15: 3 = 5 (с)
Составим выражение: 5 3: 3 = 5 (с) Ответ: 5 с потребуется слепню.
Реши задачу.
1. Катер, двигаясь со скоростью 32 км/ч, прошёл путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на лодке, если она движется со скоростью 8 км/ч?
2.Велосипедист, двигаясь со скоростью 10 км/ч, проехал путь между деревнями за 4 ч. Сколько
потребуется времени пешеходу, чтобы пройти этот же путь, если он движется со скоростью 15 км/ч?
Составные задачи на время. II тип.
Образец:
Многоножка сначала бежала 3 мин со скоростью 2 дм/м, а потом она побежала со скоростью 3 дм/м. За какое время многоножка пробежала оставшийся путь, если всего она пробежала 15 дм? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.
Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.
Скорость (V) Время (t) Расстояние (S)
С. — 2 дм/мин З мин?дм
П.-3 дм/мин? ? мин?дм 15дм
Составим план решения этой задачи. Чтобы узнать, время многоножки потом, надо узнать какое расстояние она пробежала потом, а для этого надо знать, какое расстояние она пробежала сначала.
t п S п S с
S с = V с · t
2 3 = 6 (м) — расстояние, которое пробежала многоножка сначала.
S п = S — S с
15 — 6 = 9 (м) — расстояние, которое пробежала многоножка потом.
Чтобы найти время, надо расстояние разделить на скорость.
9: 3 = 3(мин)
Ответ: за 3 мин многоножка пробежала оставшийся путь.
Реши задачу.
1. Волк бежал по лесу 3 ч со скоростью 8 км/ч. По полю он бежал со скоростью 10 км/ч.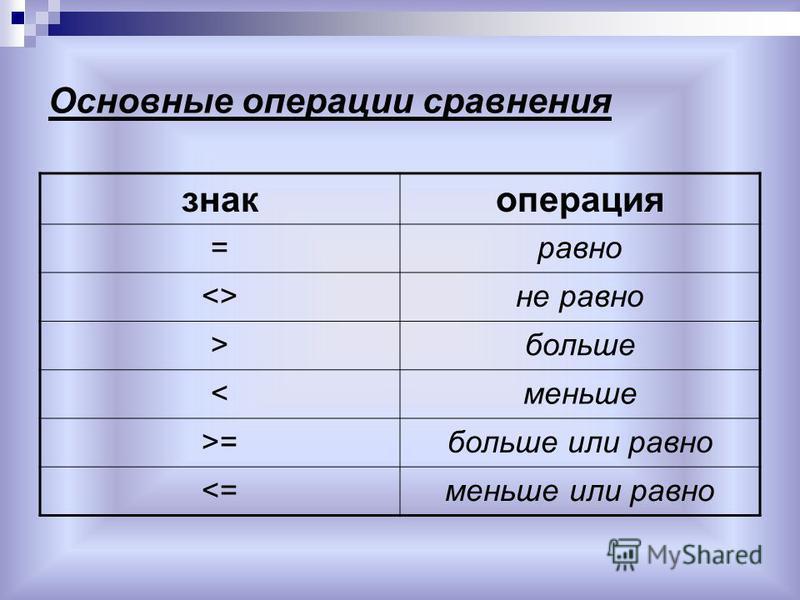 Сколько времени волк бежал по полю, если он пробежал 44 км?
Сколько времени волк бежал по полю, если он пробежал 44 км?
2. Рак до коряги полз 3 мин со скоростью 18 м/мин. Остальной путь он полз со скоростью 16 м/мин. Сколько времени потребовалось раку на остальной путь, если он прополз 118м?
3. Гена добежал до футбольной площадки за 48 с со скоростью 6 м/с, а потом он побежал к школе со скоростью 7 м/с. Через какое время Гена добежит до школы, если он пробежал 477 м?
4. Пешеход шёл до остановки 3 ч со скоростью 5 км/ч, после остановки он пошёл со скоростью 4 км/ч. Сколько времени пешеход был в пути после остановки, если он прошёл 23 км?
5. Уж плыл до коряги 10с со скоростью 8 дм/с, а потом он поплыл до берега со скоростью 6 дм/с. За какое время доплыл уж до берега, если он проплыл 122дм?
Составные задачи на скорость. I тип
Образец:
Из норки побежали два ёжика. Один бежал 6 с со скоростью 2 м/с. С какой скоростью должен бежать другой ёжик, чтобы преодолеть это расстояние за 3 с? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.
Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.
Скорость (V) Время (1) Расстояние (8)
I — 2 м/с 6 с одинаковое
II — ?м/с 3 с
Составим план решения этой задачи. Чтобы найти скорость второго ёжика, надо найти расстояние, которое пробежал первый ёжик.
Чтобы найти расстояние, надо скорость умножить на время.
S = V I · t I
2 · 6 = 12 (м) – расстояние, которое пробежал первый ежик.
Чтобы найти скорость, надо расстояние разделить на время.
V II = S: t II
12:3 = 4(м/с)
Составим выражение: 2 6:3 = 4 (м/с)
Ответ; 4м/с скорость второго ёжика.
Реши задачу.
1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?
2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы преодолеть это расстояние за 3 ч?
С какой скоростью должен идти пешеход, чтобы преодолеть это расстояние за 3 ч?
3. Автобус, двигаясь со скоростью 64 км/ч, прошёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, чтобы преодолеть это расстояние за 8 ч?
4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстояние за 6 мин?
Составные задачи на скорость. II тип
Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?
Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.
Скорость
Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая -медленее; один человек идет быстрым шагом, другой — не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то Допустим, что 5 км/ч. То есть за 1 час он прошел 5 километров.
Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то Допустим, что 5 км/ч. То есть за 1 час он прошел 5 километров.
Формула пути (расстояния) — произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время. Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».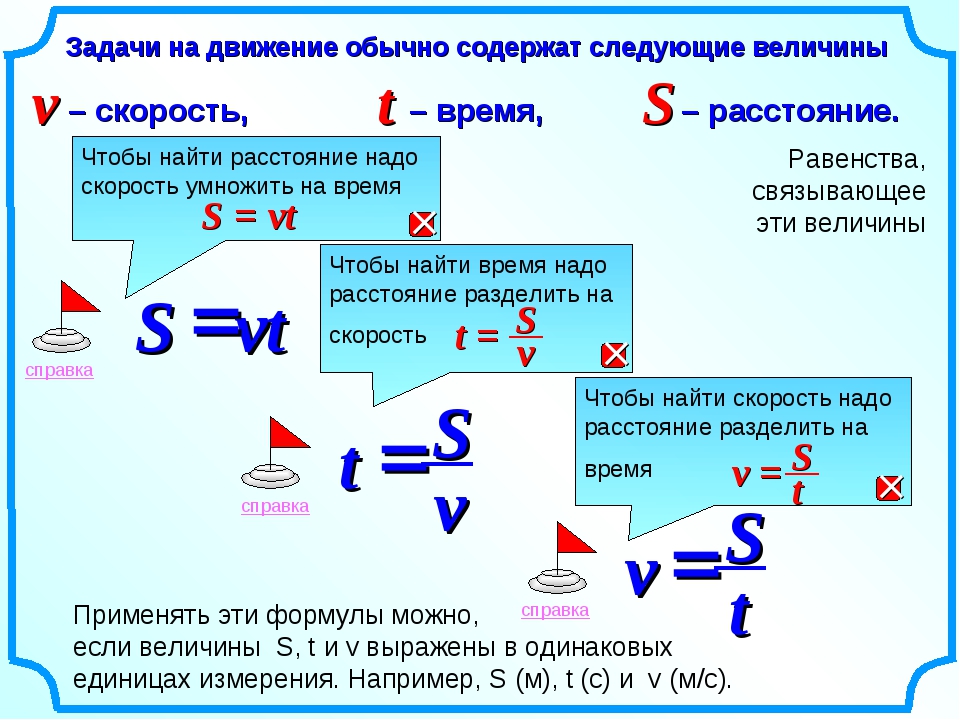
Не упустите!
Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:
Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.
Вот так легко запоминается формула «скорость, время, расстояние». Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено.
Открытый урок по математике в 4 классе на тему: Задачи на движение
Урок математики. 4 класс.
4 класс.
Тема: Задачи на движение.
Цель урока: закрепление умения решать задачи на движение.
Задачи:
Образовательные:
формировать умение решать задачи на движение; учить применять на практике ЗУН, полученные в ходе изучения данной темы.
Развивающие:
развивать внимание, память, логическое мышление; развивать математическую речь учащихся.
Воспитывающие:
воспитывать трудолюбие, ответственность; умение работать в паре и классом, слушать и слышать других.
Ход урока
I. Организационный момент
Долгожданный дан звонок,
Начинаем мы урок.
Слушайте внимательно,
Работайте старательно.
II. Сообщение темы урока.
— Посмотрите на экран, что объединяет все эти объекты? (Движение)
(На экране движущиеся объекты: велосипедист, самолет, лодка, машина, лыжник, ракета.)
— Как думаете, что мы будем делать сегодня на уроке? (Решать задачи на движение)
— Где нам может пригодиться умение решать задачи на движение?
(В жизни.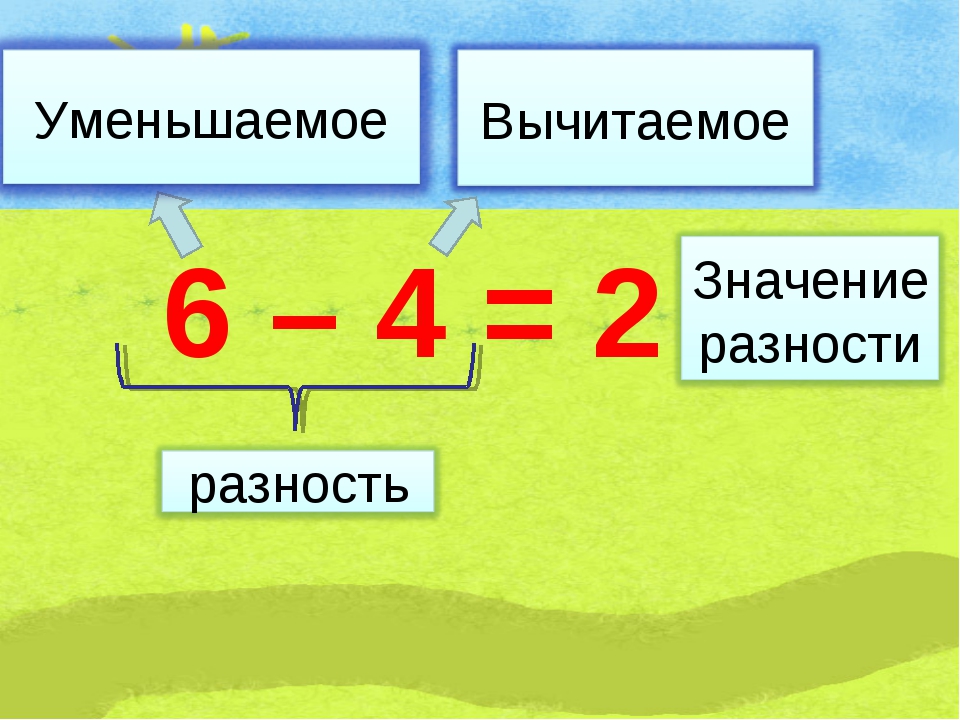 Чтобы не опаздывать на встречи, спланировать время выхода, рассчитать скорость движения)
Чтобы не опаздывать на встречи, спланировать время выхода, рассчитать скорость движения)
— Мы не просто будем решать задачи, а отправимся в путешествие. Мы поедем в нашу столицу Астану. Перед дальней дорогой нам надо немного размяться.
III. Актуализация знаний.
1. — Какие величины используются в задачах на движение? (Расстояние, скорость, время)
— Какой буквой обозначается расстояние? S
— Как его найти? ( Расстояние равно скорости, умноженной на время.)
S =V ∙ t
— Какой буквой обозначается скорость? V
— Как ее найти? (Скорость равна расстоянию, деленному на время.)
V = S : t
— Какой буквой обозначается время? t
— Как его найти? (Время движения равно расстоянию, деленному на скорость)
t = S : V
2. Раздели данные единицы измерения на три группы.
Км/мин мм сек неделя см м/сек
— По какому признаку вы их разделили на 3 группы? (Единицы измерения расстояния, скорости, времени)
— Какими еще единицами измерения можно добавить каждую группу?
3. Математический диктант.
Математический диктант.
• Мы летели на самолёте 3 часа со скоростью 900км/ч. Какое расстояние мы пролетели?
• Поезд за 4 часа прошёл 360 км. С какой скоростью он двигался?
• За какое время прошел турист 28 км, если он шел со скоростью 4 км/ч?
• Какое расстояние проплывет катер за 4 часа, если он движется со скоростью 30 км/ч?
• Мотоциклист за 4 часа проехал 320 км. С какой скоростью он двигался?
• Крейсер проплыл 80 км со скоростью 40 км/ч. Сколько времени он затратил?
• За 2 часа вертолет пролетел 600 км. С какой скоростью он летел?
• Какое расстояние пройдет лыжник за 5 часов, если будет двигаться со скоростью 15 км/ч?
• Расстояние от города до поселка 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 6 км/ч?
4. — Какие существуют виды задач на движение?
• Движение навстречу друг другу (на сближение)
• Движение в противоположные стороны (на удаление)
• Движение друг за другом
— Что общего в этих задачах?
(Есть объекты движения, есть величины: скорость, время, расстояние)
— Чем отличаются эти задачи?
(Направление движения объектов)
IV. Решение задач
Решение задач
— Я вижу, вы готовы отправиться в путешествие. Нам необходимо узнать, какое расстояние мы с вами должны преодолеть, для этого вы должны решить задачу.
1. Самостоятельная работа.
Задача.
Расстояние от г. Петропавловска до г. Кокшетау можно преодолеть за 2 ч со скоростью 90км/ч и расстояние от г. Кокшетау до г. Астаны за 4 ч со скоростью 75км/ч. Найди расстояние между г. Петропавловском и г. Астаной.
Проверка решения.
— Что находили? (Расстояние)
— Как находили? (S =V ∙ t )
90∙2=180 (км) – расстояние между Петропавловском и Кокшетау
75∙4=300 (км) – расстояние между Кокшетау и Астаной
180+300=480 (км) – расстояние между Петропавловском и Астаной
2. Физкультминутка.
— Мы сегодня говорим о движении, и мы должны знать правила дорожного движения. Вот мы сейчас с вами и повторим эти правила в нашей физкультминутке. Да – хлопать в ладоши, нет – топать.
• Пешеходы должны пересекать проезжую часть по пешеходным переходам.
• Выезжать за пределы дворовой территории можно детям с 7 лет.
• Можно играть на проезжей части дороги и на тротуаре.
• Переходить улицу можно только при зеленом свете светофора.
• Переходя через улицу, сначала посмотри направо.
• Нельзя обходить автобус, троллейбус, трамвай ни спереди, ни сзади. Для того чтобы перейти дорогу, необходимо дойти до ближайшего пешеходного перехода.
• Красный сигнал светофора означает: движение транспорта запрещено.
3. Работа в группах.
— Итак, мы отправляемся в путь. А сейчас будем работать в группах. На столе лежит карточка с задачей и план работы.
Задача.
Мы выехали из Петропавловска, навстречу нам из Астаны выехали наши друзья. Через сколько часов мы встретимся, если мы будем ехать со скоростью 85 км/ч, а наши друзья со скоростью 75 км/ч? Расстояние между городами мы нашли в первой задаче.
План работы:
• Определить вид задачи.
• Сделать чертёж и соответствующие надписи на чертеже.
• Решить задачу по действиям с пояснениями.
Проверка решения.
Ответы учащихся. (Эта задача на встречное движение. Для того чтобы решить задачу такого вида, нам необходимо, сначала найти скорость сближения, а затем расстояние разделить на полученный результат.)
75+85=160 (км/ч) – скорость сближения
480:160=3 (ч) – время
4. Коллективный разбор задачи и самостоятельная запись решения.
— Продолжаем наше путешествие. По дороге мы встретили двух велосипедистов. Они выехали одновременно из поселка в одном направлении. Скорость первого 13км/ч, скорость второго 11км/ч. Какое расстояние будет между ними через 3 часа?
— В каком направлении двигаются велосипедисты? (Одновременно, в одном направлении.)
— Какова скорость первого велосипедиста? (13км/ч)
— А скорость второго?( 11км/ч)
— Что еще известно в задаче? (Время)
— Что нужно найти в задаче? (Расстояние)
— Как будем решать? Что сначала узнаем в задаче? (Скорость удаления)
— Как найти скорость удаления при движении в одном направлении? (Из скорости первого вычесть скорость второго)
— Как найти расстояние? (Расстояние равно скорости, умноженной на время)
13-11=2 (км/ч) – скорость удаления
2∙3=6 (км) – расстояние между велосипедистами через 3 часа
5. Решение задачи вдогонку.
— По дороге мы встретили водителей легкового и грузового автомобилей. Они обратились с просьбой. Мы должны помочь им узнать скорость грузовика.
Задача.
Из двух пунктов, расстояние между которыми 150 км, выехали одновременно в одном направлении легковой автомобиль и грузовик. Через 5 часов легковой автомобиль догнал грузовик. Найдите скорость грузовика, если скорость легкового автомобиля 80 км/ч.
— Как двигаются объекты? (Вдогонку.)
— Какую скорость находим? (Скорость сближения.)
— Как найдем скорость сближения?
— Как найдем скорость грузовика?
150:5=30 (км/ч) – скорость сближения
80-30=50 (км/ч) – скорость грузовика
V. Подведение итогов
— Вот наше путешествие подходит к концу. Вы молодцы! Справились со всеми заданиями. Ребята, понравился вам наш урок?
VI. Рефлексия.
Закончи предложение:
• Для меня было интересным….
• Я не знал(а) что….
• Труднее всего было…
• Я точно запомнил(а), что….
V. Домашнее задание.
Составить и решить задачу на движение.
«Задачи на движение» 4 класс
Конспект открытого урока математики
на тему: «Задачи на движение»
4 класс
Цель урока: закрепление умения решать задачи на движение.
Задачи:
Образовательные:
формировать умение решать задачи на движение; учить применять на практике ЗУН,
полученные в ходе изучения данной темы.
Развивающие:
развивать внимание, память, логическое мышление; развивать математическую
речь учащихся.
Воспитывающие:
воспитывать трудолюбие, ответственность; умение работать в паре и классом,
слушать и слышать других.
Тип урока: закрепление.
- Орг. момент
— Я рада всех вас видеть на нашем уроке. Я желаю вам хорошего настроения и отличных ответов. Повернитесь к своему соседу, улыбнитесь. Пожелайте ему удачи.
2. Актуализация знаний.
А сейчас небольшая разминка перед серьёзной работой.
— Правила игры следующие: я задаю вопросы, кто первым правильно поднимет руку и правильно ответит , тот перемещается на свободное место.
1. Чтобы узнать скорость надо…(S:t)
2. чтобы узнать время надо…(S:V)
3. Чтобы узнать расстояние надо…(V*t)
4. км\ч- это ед. измерения…(скорости)
5. час, мин- это ед. измерения…(времени)
6. м\мин- это ед. измерения… (скорости)
7. м, км- это ед. измерения …(расстояния)
8. S=12км, t=6 ч. Чему равна скорость?
9. V=5км/ч, t=5ч.Чему равно расстояние?
10. V=3км\ч, S=15км.Чему равно время?
11. Как найти скорость сближения или отдаления? (сумма скоростей)
12. За 5 секунд заяц пробегает 100 метров. Найти скорость зайца. (20 м/сек)
13. За какое время охотник , двигаясь на лыжах со скоростью 7 км/ч, пройдёт 14 км? (2 часа)
-Молодцы! Займите все свои места.
Встаньте те, кто переместился больше 3 раз, 2 раза, 1 раз.
-Оцените свою работу в графе «устный счёт» в баллах. Те кто переместился 1 и более раз ставят 5 баллов, не переместился- 0 баллов.
3. Самоопределение к деятельности.
· Верно ли что, расстояние в 12 км пешеход преодолеет за 3 часа, если будет двигаться со скоростью 4 км/ч? · Турист прошёл 25км за 5 часов. С какой скоростью шёл турист? Выберите верный ответ. а) 125 км/ч б) 25 км/ч в) 20 км/ч г) 5 км/ч · Назовите только арифметическое действие ( +, — , ×, ÷), которое необходимо, чтобы ответить на вопрос задачи. Слон двигался со скоростью 100м/мин. Какое расстояние он прошёл за 10 минут? · Расстояние от школы до дома, где живёт ученик 4 класса Фролов Данил 800 м. Сколько времени нужно, Данилу, чтобы дойти до школы, если он идёт со скоростью 40 м / мин? · Выбери расстояние, которое может быть между двумя городами. |
а) 120 м
б) 120 дм
в) 120 км
· Верно ли что, чтобы вычислить время движения, нужно скорость разделить на расстояние?
· Верно ли что, скорость движения пешехода может быть 70 км/ч?
· На участке дороги длиной 270 км стоит знак ограничения скорости до 60 км/ч. Нарушил ли его водитель, если это расстояние он преодолел за 4 часа?
· Верно ли что, чтобы вычислить время движения, нужно скорость разделить на расстояние?
· Верно ли что, скорость движения пешехода может быть 70 км/ч?
· На участке дороги длиной 270 км стоит знак ограничения скорости до 60 км/ч. Нарушил ли его водитель, если это расстояние он преодолел за 4 часа?
— Какой же темой объединены все эти задания?
-Подумайте, ребята, нужны ли нам умения решать задачи на движение?
— Зачем они нам? (чтобы не опаздывать на встречи, уметь спланировать время выхода, рассчитать скорость движения, чтобы не было аварий, и т.д.)
— Вспомним, что нам уже известно о задачах на движение.
— Что общего и в чём различия этих задач?
ОБЩЕЕ: есть объекты движения, есть величины: скорость, время, расстояние
РАЗЛИЧИЯ: направление движения объектов, место отправления значения величин и единицы их измерения.
— Какие формулы необходимо помнить?
Какие существуют виды задач на движение?
Движение в противоположном направлении с удалением
Движение в противоположном направлении навстречу друг другу
Движение в одном направлении с отставанием
Движение в одном направлении вдогонку
4. Постановка учебной задачи.
—
Чем мы сегодня будем заниматься на ? Решать задачи на все виды движения.
1. — Какие величины используются в задачах на движение? (Расстояние,
скорость, время)
— Какой буквой обозначается расстояние? S
— Как его найти? ( Расстояние равно скорости, умноженной на время.)
S =V ∙ t
— Какой буквой обозначается скорость? V
— Как ее найти? (Скорость равна расстоянию, деленному на время.)
V = S : t
— Какой буквой обозначается время? t
— Как его найти? (Время движения равно расстоянию, деленному на скорость)
t = S : V
2. Раздели данные единицы измерения на три группы.
Км/мин мм сек неделя см м/сек
— По какому признаку вы их разделили на 3 группы? (Единицы измерения
расстояния, скорости, времени)
— Какими еще единицами измерения можно добавить каждую группу?
3. — Какие существуют виды задач на движение?
• Движение навстречу друг другу (на сближение)
• Движение в противоположные стороны (на удаление)
• Движение друг за другом
— Что общего в этих задачах?
(Есть объекты движения, есть величины: скорость, время, расстояние)
— Чем отличаются эти задачи?
(Направление движения объектов)
5. Физкультминутка
Мы считали и устали,
А сейчас мы дружно встали.
Ручками похлопали — раз, два, три.
Ножками потопали — раз, два, три.
Головкой покачали — раз, два, три.
Сели, встали, встали, сели,
Никого мы не задели.
Мы немножко отдохнем
И опять решать начнем.
6.
Решение задач
Задача
1 Два зайца выскочили из куста, испугались друг друга и понеслись в разные
стороны. Скорость первого зайца 580 м/мин, а скорость второго зайца 520 м/мин.
На каком расстоянии друг от друга они будут через 1час ? Выбери и запиши
выражение к задаче:
1. (580 + 520) : 60
2. (580 + 520) ∙ 60
3. (580 + 520) ∙100
4. 580 x 60 + 520 ∙ 60
-Какой вид движения в задаче?
— Что нашли 1 действием?
— Почему умножили на 60?
Задача
2 Миша и Петя катались на велосипедах. Петя уехал вперёд. Миша решил догнать
своего друга, когда между ними было расстояние 30 м. При каком условии Миша
догонит Петю? (Если скорость Миши будет больше скорости Пети) Через сколько
минут произойдёт встреча? (Проблема!)
— Каких данных не хватает в условии задачи, чтобы ответить на второй вопрос?
(Не известны скорости велосипедистов)
— Чтобы узнать с какой скоростью двигался каждый мальчик вы должны решить
уравнения по вариантам. Затем, узнав ответ своего соседа по парте, решить нашу
задачу.
Взаимопроверка.
—
Проверяем решение задачи.
1) 24 — 18 = 6 (м/мин) – скорость сближения
2) 30 : 6 = 5 (мин)
-Молодцы!
-Давайте ребята ещё раз назовём формулы нахождения времени, скорости и расстояния.
V=S : t
S=V* t
t=S :V
— Ребята, давайте вспомним, какую цель мы ставили перед собой в начале урока?
-Как вы думаете, мы достигли этой цели?
7. Работа по карточкам
— Перед вами три карточки: на “5 — красная — повышенной сложности”, на “4 — синяя – средней сложности” и на “3 — зеленая – простая задача”. Выберите ту, с которой вы, по-вашему, можете справиться и решите задачу.
Задача на “3” — зеленая Простая задача
Велосипедист проехал 48 км за 4 часа. С какой скоростью он двигался?
48 : 4 =12 (км/ч)
Ответ: 12 км/ч
Задача на “4” — синяя Средней сложности
Дачник ехал от города до деревни 2 часа на автобусе со скоростью
60 км/ч, а потом шёл 7 километров пешком. Найдите расстояние от города до деревни.
60 * 2 = 120(км)
120 + 7 =127(км)
Ответ: 127 км
Задача на “5” — красная Повышенной сложности
Велосипедист проехал 24 км со скоростью 12 км/ч, а потом еще 45 км со скоростью 15 км/ч. Сколько времени он был в пути?
1) 24:12 = 2(ч)
2) 45:15 = 3(ч)
3) 2 + 3 =5(ч)
Ответ: 5 часов
Проверка: Поднимите руку кто решал задачу на красной карточке- проверим решение (на доске правильное решение) (на слайде)
Кто решал задачу на синей карточке – проверим решение;
Кто решал задачу на зеленой карточке – проверим решение
8. Рефлексия.
— Чему мы учились на уроке?
— Что вам понравилось?
Что было трудно?
9. Домашнее задание.
— Вы сегодня хорошо потрудились. Решили много интересных задач . Предлагаю вам дома продолжить работу по выбору.
Спасибо за урок!
Простейшие уравнения с модулем. Тест
Определение. Геометрический смысл
Модуль (или абсолютная величина) числа (обозначается как )— неотрицательное число, определение которого зависит от типа числа
А именно:
Мы будем называть данное правило правилом раскрытия модуля.
Например, так как , попадаем в первую строку (ситуацию).
так как попадаем во вторую ситуацию.
С геометрической точки зрения, – есть расстояние между числом и началом координат.
Решением уравнения, например, являются числа и , потому что расстояние от точки координатной прямой до нуля равно , и расстояние от точки до нуля также равно 6.
|| с геометрической точки зрения означает расстояние между точками и .
Полезные примеры
1) Раскрыть модуль:
Так как больше, чем , то , а значит согласно правилу раскрытия модуля.
2) Раскрыть модуль:
Так как больше нуля при всех значениях , то согласно правилу раскрытия модуля.
3) Раскрыть модуль:
Так как , то , а значит, согласно правилу раскрытия модуля.
Решение уравнений
1) Решить уравнение .
Модуль – всегда неотрицательная величина, поэтому уравнение решений не имеет.
Ответ: { }
2) Решить уравнение: .
Модуль раскрывается таким образом в случае, когда .
Ответ:
3) Решить уравнение:
Согласно геометрическому смыслу модуля левая и правая части равенства представляют из себя одно и то же.
Ответ:
4) Решить уравнение:
Раскрываем модуль согласно правилу раскрытия модуля:
а)
Имеем: ,
Откуда .
Поскольку мы находимся в ситуации , то подходит только корень .
б)
Имеем: ,
Откуда или .
Поскольку мы находимся в ситуации , то ни один корень из найденных в пункте (б) нам не подходит.
Ответ: .
Коротко можно было бы решение оформить так:
5) Решить уравнение:
Раскрываем модуль согласно правилу раскрытия модуля:
a) Первый случай:
Что равносильно .
б) Второй случай:
Что равносильно
Ответ:
6) Решить уравнение:
Можно было бы действовать согласно правилу раскрытия модуля, но проще будет в данном случае рассуждать так:
Внутри модуля может «скрываться» как так и .
Поэтому или
или
Из первого уравнения или , а второе уравнение корней не имеет.
Ответ:
7) Решить уравнение:
Раскрываем модуль согласно правилу раскрытия модуля:
а) Первый случай:
Рассмотрим отдельно первую строку системы:
Рассмотрим уравнение из системы:
или
Разложим на множители левую часть уравнения способом группировки, предварительно разбив среднее слагаемое на два:
Откуда (трехчлен в скобках корней не имеет).
Данный корень удовлетворяет первой строке системы, он пойдет в ответ.
б) Второй случай:
Решение неравенства системы:
Корень удовлетворяет решению неравенства системы.
Собираем решения.
Ответ:
Также, смотрите «Модуль. Простейшие неравенства с модулем» здесь.
Вы можете пройти тест по теме «Модуль. Раскрытие модуля. Простешие уравнения с модулем»
Как обозначается скорость время расстояние. Примеры из жизни
Однажды случайный прохожий спросил Эзопа: «Как скоро я доберусь до города?» Эзоп ответил: «Не знаю». Прохожему ничего не оставалось, как только пойти дальше своей дорогой – и тогда Эзоп крикнул ему вслед: «Ты дойдёшь до города к полудню!» Прохожий удивился: «Почему же ты не ответил мне сразу, если знал ответ?» И Эзоп сказал: «Как же я мог сказать это, не зная, как ты ходишь?»
Действительно, о том, что время, расстояние и скорость – величины взаимосвязанные, известно давно. Из этого логически следует, что зная две из них, можно вычислить третью. Формула тоже представляется предельно логичной: если скорость равна, например, 60 км/ч (возьмём для примера разрешённую скорость автомобиля в городе) – т.е. за час он проезжает 60 километров, то для нахождения расстояния, которое он преодолеет за два часа, нам надо всего лишь умножить шестьдесят на два – в результате мы получаем 120 километров.
Представим это в виде формулы. Расстояние в физике принято обозначать латинской буквой S – почему так, с точностью сказать нельзя, это связывают и с немецким словом «Spur», что переводится как «колея» или «след», и с латинскими словами «sulcus» – что значит «борозда» – и «semita», переводимом как «тропинка» или «путь». Яснее происхождение обозначений для других составляющих этой формулы. Время обозначается латинской буквой t – от латинского слова «tempus», которое, собственно и означает – «время» (к нему же восходит музыкальный термин «темп» – хотя в этом можно усмотреть некоторую «путаницу»: темп в музыке – это всё-таки ближе к понятию скорости, чем времени). Время же – латинская буква v – что опять же связано с латынью: «скорость» на этом языке именуется «velocitas».
Итак, формула расстояния выглядит следующим образом: v×t=s
Исходя из этого – и зная правила умножения и деления, разумеется, которые изучают во втором классе, когда и начинают решать такие задачи – мы легко можем найти и другие составляющие. Как мы помним из начальной школы, чтобы вычислить один из множителей, необходимо разделить произведение (т.е. результат умножения) на другой из них. Иными словами, делим расстояние (s) на время (t) – получаем скорость (v), если же нам нужно вычислить время(v) – поступаем наоборот, т.е. делим расстояние на время.
Ничего сложного в таких вычислениях нет – так что с ними с лёгкостью справляются уже второклассники… правда, такая формула предполагает, что объект, с которым мы имеем дело, постоянно движется с одной и той же скоростью (такое движение в физике называется равномерным) – что далеко не всегда имеет место в реальности. Что делать, если скорость движущегося тела изменяется – как бывает, например, когда автомобиль трогается с места?
Тут мы уже имеем дело с более сложной формулой – а именно, с формулой равноускоренного движения, для которого приходится ввести новую величину – ускорение, традиционно обозначаемое латинской буквой a. Чтобы вычислить расстояние при равноускоренном движении (при условии, что тело стартует из состояния покоя), нам придётся умножить ускорение на возведённое в квадрат время, а результат разделить на два.
Остаётся один вопрос – как вычислить ускорение? Для этого надо знать начальную скорость и конечную, соотношение между которыми характеризуется такой формулой:
(v – это конечная скорость, а v0 – начальная). «Вытащить» ускорение из этой формулы – не проблема: из конечной скорости вычитаем начальную и делим результат на время.
Остаётся только добавить, что формулами, характеризующими равноускоренное движение, мы обязаны Г.Галилею, который изучал это явление на примере ускорения при свободном падении.
Цель : продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Задачи :
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел — скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование : карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
учебник.
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы : формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.
Учитель : Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисел 51300 и 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам — шофер (Имитируют управление автомобильным рулем.)
И сам — мотор. (Круговые движения плечами вперед-назад.)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Слайд № 6
Решение задачи № 2
Автобус
S — 90 км 90: 45= 2 часа
T — ?
V — 45 км/ч
Легковая машина
S — 270 км 270: 90 = 3 часа
T — ?
V — 90 км/ч
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный — радость
- Жёлтый — приятное
- Зелёный — спокойное
- Синий — грустное
- Фиолетовый — тревожный
- Оранжевый — удовлетворение
- Чёрный — неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок —
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость — это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
- S – пройденный телом путь,
- t – время движения.
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с). В то же время общепризнанными единицами измерения являются километр в час (км/ч), узел (морская миля в час).
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Сравните скорость Зелибобы и Кубика. ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, служащие для записи математических понятий, предложений и выкладок.
Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Кириллические буквы сейчас очень редко используются для обозначения физических величин, хотя частично применялись в русскоязычной научной традиции. Поскольку скорость света в вакууме – величина постоянная, в расчетах она принимается за константу. Скорость это величина, которая характеризует быстроту перемещения объекта относительно выбранной системы отсчета.
какой буквой в алгебре обозначается время
Самая простая формула скорость, это длина деленная на расстояние. Латинской буквой V. Такое обозначение используется и в математике, и в физике. Начатки буквенного обозначения и исчисления возникают в позднеэллинистич.
В различных странах стихийно появляются 3. м. для нек-рых действий и для степеней неизвестной величины. Кто готов назвать их в порядке возрастания? В единицах длины).
Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы. Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. Вы назвали формулу, по которой находят скорость движения. Этой формулой вы будете пользоваться и в старших классах.
Урок математики в 3-м классе по теме «Скорость. Время. Расстояние»
S ׃ t 24 ׃ 4 = 6 (м/мин) скорость Кубика. Вывод: Скорость – это величина, которую можно измерить и сравнить. Вместе с вами они научились измерять скорость движения. Давайте потренируемся в решении задач на нахождение скорости, выполняя работу самостоятельно. Бусинка вам предлагает найти скорость движения своих друзей в других видах спорта.
Как будете находить скорость движения? Будьте внимательны при обозначении скорости. Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения? Цель: продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Какой буквой обозначается скорость?
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Когда такая связь существует, это обозначено в скобках.
В круглых скобках указывается одна или несколько переменных, от которых зависит физическая величина. Диакритические знаки добавляются к символу физической величины для обозначения определённых различий.
Как обозначается время
Все мы прекрасно помним еще со школы, чтобы найти Скорость (V), нужно Расстояние (S) разделить на Время (t), которое затратили на преодоление этого расстояния (пути). Скорость величина векторая, так что зачастую требуется указывать направление скорость.
Дата и время в английском языке
Очень часто люди путают скорость с ускорением, что приводит плохим последствиям. Развитие математической символики было тесно связано с общим развитием понятий и методов математики. Первые 3. м. для произвольных величин появились много позднее (начиная с 5-4 вв. до н. э.) в Греции. Произвольные величины (площади, объемы, углы) изображались в виде отрезков, а произведение двух произвольных величин — в виде прямоугольника, построенного на соответствующих отрезках.
14-17 вв.; оно определялось успехами практич. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный для исчисления символ. Вслед за Леонардо Пизанским (Leonardo Pisano, 1220) многие обозначали (вплоть до 17 в.) квадратный корень знаком (от лат. radix — корень). Весьма различны были 3. м. неизвестной и ее степеней. Значительным шагом вперед в развитии математич.
Дальнейшее развитие 3. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики к-рого основа была уже в большой мере подготовлена в алгебре. Благодаря этому знак годится и для записи формул замены переменных и легко может быть использован для записи кратных и криволинейных интегралов.
Огромная заслуга в создании символики современной математики принадлежит Л. Эйлеру (L. Euler). В 19 в. роль символики еще более возрастает и, наряду с созданием новых 3. м., математики стремятся к стандартизации основных символов. С точки зрения математической логики, среди 3. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений.
Время передачи “Улицы Сезам” истекает. Обычно в физике скорость обозначается латинской буквой v. Иногда эту букву пишут прописной, иногда строчной. Основной его расшифровкой служит определение: Скорость — это отношение пройденного пути (расстояния) за определенный промежуток времени.
Расстояние в математике: формула и концепция — видео и стенограмма урока
Примеры расстояний
1.) Найдите расстояние между заданными точками на этом графике:
Координаты двух точек:
( x 1, y 1) = (2, 5)
( x 2, y 2) = (9, 8)
Чтобы решить это уравнение, вам просто нужно подставить числа в формулу расстояния, которую мы рассмотрели ранее.2)
d = √ (49 + 9)
d = √ (58)
d = 7,6
2.) Найдите расстояние между двумя точками на графике:
В этом примере точки:
(-1, 2) и (2, 1)
При использовании формулы расстояния с отрицательными числами очень важно работать осторожно, чтобы не потерять отрицательные по пути.
Давайте подставим наши значения в формулу расстояния, а затем упростим, как и раньше:
d = √ (2 — (-1)) ^ 2 + (1-2) ^ 2
d = √ (3 ^ 2 + (-1) ^ 2)
d = √ (9 + 1)
d = √ (10)
d = 3.2
Если вы пытаетесь определить расстояние между двумя точками, находящимися на прямой горизонтальной или вертикальной линии, вы можете просто подсчитать количество пробелов между точками. Формула расстояния также будет работать; однако вероятность ошибки также возрастает.
3.) Найдите расстояние между двумя точками на следующем графике:
Поскольку точки расположены на прямой линии, довольно легко посчитать расстояние между ними и получить ответ — 3.2
d = √ (0+ 9)
d = √ (9)
d = 3
Происхождение формулы расстояния
Формула расстояния получена из теоремы Пифагора . Вы можете вспомнить, что теорему Пифагора можно использовать, чтобы найти длину любой одной стороны прямоугольного треугольника, если вы знаете две другие стороны. Чтобы использовать эту формулу для получения формулы расстояния, просто выполните следующие действия. 2
Резюме урока
Теперь, когда этот урок закончен, вашей целью должно быть понимание следующей информации:
- Определите, как измерить расстояние с помощью математики
- Определите формулу расстояния, которую вы используете, если хотите определить расстояние между двумя точками на координатной плоскости
- Опишите примеры формулы
- Объясните, откуда взялась формула
Математическое расстояние определяется как расстояние между двумя точками.Это расстояние можно вычислить с помощью формулы расстояния, которая является производным от теоремы Пифагора , которая используется для определения длины любой одной стороны прямоугольного треугольника, когда вы знаете две другие стороны.
Формула расстояния | Purplemath
Purplemath
Формула расстояния — это вариант теоремы Пифагора, которую вы использовали еще в геометрии.Вот как мы переходим от одного к другому:
Предположим, вам даны две точки (–2, 1) и (1, 5), и они хотят, чтобы вы выяснили, насколько они далеко друг от друга. Очки выглядят так:
MathHelp.com
Вы можете рисовать линии, образующие прямоугольный треугольник, используя эти точки как два угла:
Легко найти длины горизонтальной и вертикальной сторон прямоугольного треугольника: просто вычтите значения x и значения y :
Затем используйте теорему Пифагора, чтобы найти длину третьей стороны (которая является гипотенузой прямоугольного треугольника):
…so:
Этот формат всегда верен. Имея две точки, вы всегда можете построить их, нарисовать прямоугольный треугольник, а затем найти длину гипотенузы. Длина гипотенузы — это расстояние между двумя точками. Поскольку этот формат работает всегда, его можно превратить в формулу:
Формула расстояния: учитывая две точки ( x 1 , y 1 ) и ( x 2 , y 2 ), дается расстояние d между этими точками. по формуле:
Пусть вас не пугают индексы.Они только указывают на то, что есть «первая» точка и «вторая» точка; то есть у вас есть два очка. Какой из них вы назовете «первым» или «вторым» — решать вам. В любом случае расстояние будет таким же.
Найдите расстояние между точками (–2, –3) и (–4, 4).
Я просто подставляю координаты в формулу расстояния:
Тогда расстояние будет sqrt (53), или около 7.28 с округлением до двух десятичных знаков.
URL: https://www.purplemath.com/modules/distform.htm
Формула расстояния| Калькулятор и пошаговые примеры // Tutors.com
Калькулятор формул расстояния
D = (х2 — х1) 2 + (у2 — у1) 2
Расстояние = (x2 − x1) 2+ (y2 − y1) 2 −−−−−−−−−−−−−−−−−− √Distance = (x2 − x1) 2+ (y2 − y1) 2
Как это работает: Введите две координаты x и две координаты y в поля ниже, и программа автоматически рассчитает расстояние между этими двумя точками и покажет вам шаг за шагом.
Ответ
(0−0) 2+ (0−0) 2 −−−−−−−−−−−−−−−− √0 – √ = 0 (0−0) 2+ (0−0) 20 = 0
Содержание
- Видео
- Калькулятор формул расстояния
- Расстояние между двумя точками
- Формула расстояния
Расстояние между двумя точками
В декартовой сетке достаточно просто измерить вертикальный или горизонтальный отрезок линии. Вы можете подсчитать расстояние вверх и вниз по оси Y или по оси X.
А как насчет диагональных линий? Как узнать, какой длины будет отрезок линии, если он пересекает эти крошечные прямоугольники? См. Этот пример:
Вы можете использовать формулу расстояния для вычисления любого отрезка линии, если знаете координаты двух конечных точек. Вы будете мысленно строить прямоугольный треугольник, используя диагональ, как если бы это была гипотенуза.
Формула расстояния
Формула расстояния возводит в квадрат разности между двумя координатами x и двумя координатами y, затем складывает эти квадраты и, наконец, извлекает их квадратный корень, чтобы получить общее расстояние по диагональной линии:
D = (х2 — х1) 2 + (у2 — у1) 2
Выражение (x2 — x1) читается как изменение x и (y2 — y1) изменение y .
Как использовать формулу расстояния
На самом деле это вычисляет расстояние по горизонтали между значениями x, как если бы линейный сегмент составлял сторону прямоугольного треугольника, а затем проделывает это снова со значениями y, как если бы вертикальный линейный сегмент был второй стороной прямоугольный треугольник.
Остается вычислить гипотенузу, заданную вами диагональ. Формула расстояния — это специальное приложение теоремы Пифагора.
Все, что вам нужно сделать, это очень аккуратно ввести координаты.Давайте использовать конечные точки нашей строки (1, 3) и (7, 6):
D = (7-1) 2 + (6-3) 2
Д = (6) 2 + (3) 2
D = 36 + 9
D = 45
D ≅ 6,7085
Примеры формул расстояния
Для использования формулы расстояния вам даже не нужно иметь координатную сетку, если у вас есть оба набора координатных точек. Итак, попробуйте эти три практических задачи!
- (-2, 4) и (10, 1)
- (5, 5) и (1, 10)
- (-11, -2) и (-21, -6)
Не оставим вас болтаться по диагонали.Вот первые шаги, которые помогут вам начать работу:
- D = (10 — -2) 2 + (1 — 4) 2
- D = (2–5) 2 + (10–5) 2
- D = (-21 — -11) 2 + (-6 — -2) 2
Что будет дальше?
- D = (12) 2 + (-3) 2
- D = (-3) 2 + (5) 2
- D = (-10) 2 + (-4) 2
Вы действительно должны уметь делать последние несколько шагов самостоятельно. Посмотрим, получили ли вы эти ответы:
- 153 ≅ 12,369
- 34 ≅ 5,8 309
- 116 ≅ 10.7703
Пифагор
Формула расстояния получает свою точность и совершенство благодаря концепции использования углового отрезка прямой, как если бы это была гипотенуза прямоугольного треугольника, образованного на сетке. Вам не нужно строить две другие стороны для применения формулы расстояния, но вы можете видеть эти две «стороны» в разностях (расстояниях) между значениями x (горизонтальная линия) и значениями y (вертикальная линия).
Краткое содержание урока
Теперь, когда вы проработали урок и практику, вы можете применить формулу расстояния к конечным точкам любого сегмента диагональной линии, появляющегося в координатной или декартовой сетке.Вы также можете связать формулу расстояния с теоремой Пифагора.
Пифагор, без сомнения, был щедрым и блестящим математиком, но он не сделал большого скачка в применении теоремы Пифагора к координатным сеткам. Чтобы вывести нас из его теоремы о соотношении сторон прямоугольных треугольников к координатным сеткам, математический мир должен был дождаться Рене Декарта. Его декартова сетка сочетает в себе геометрию и алгебру. Вы можете использовать формулы, в том числе формулу расстояния, чтобы получить точные измерения отрезков линии на сетке.
Следующий урок:
Что такое прямая линия?
Обучение абсолютному значению числа в математике
Урок 2: Разработка концепции
Материалы: Каталожные карточки или цифровые «карточки», которые могут быть распределены среди класса
. Стандарты:
- Под абсолютным значением рационального числа понимается его расстояние от 0 на числовой прямой. (6.NS.C.7.C)
Подготовка: Сделайте карточки для У меня есть… У кого есть?
Заключительная и оценочная игра
- Попросите учащихся написать и поделиться своими определениями и примерами из реальной жизни ситуаций абсолютной ценности.
- Играть У меня есть … у кого есть? Составьте набор из 15 учетных карточек с уравнениями абсолютных значений и 15 учетных карточек, содержащих значения переменной. Если учетные карточки недоступны или вы адаптируете это для дистанционного обучения, создайте способ, чтобы 30 приведенных ниже уравнений были распределены среди ваших учеников как можно более равномерно.
| Карты абсолютного значения | Карты переменного значения |
| | x + 5 | = 20 | x = 15 |
| | 5 — x | = 30 | x = –25 |
| | x + 6 | = 41 | x = 35 |
| | –27 — x | = 20 | x = –47 |
| –7 + | x | = 0 | x = –7 |
| | 25 — x | = 18 | x = 7 |
| | x + –5 | = 38 | x = 43 |
| | 37 — x | = 70 | x = –33 |
| 114 — | x | = 7 | x = 107 |
| | — x + 100 | = 21 | x = 121 |
| — | 1 + x | = -80 | x = 79 |
| | x | = 81 | x = –81 |
| | x + 3 | = 84 | x = 81 |
| | 25 + x | = 62 | x = –87 |
| | x — 26 | = 11 | x = 37 |
Каждая указанная карта абсолютного значения имеет два значения: x .Эти значения перекрываются, так что каждая карта значений переменных удовлетворяет двум из заданных уравнений абсолютного значения (первое и второе значения удовлетворяют первому уравнению, второе и третье значения удовлетворяют второму уравнению и т. Д., Пока последнее и первое значения не удовлетворяют условиям последнее уравнение).
Распределите карточки или уравнения поровну. Убедитесь, что все они были розданы. Выберите ученика, который скажет «У меня есть», а затем прочтите значение или уравнение на его карточке. Затем попросите учащегося сказать: «У кого есть совпадение для моей карты?» Любой ученик, у которого есть совпадение, должен сказать: «У меня есть… у кого есть…», и игра продолжается до тех пор, пока не будут прочитаны все карточки.Вы можете попросить учеников встать, когда игра начинается, и сесть, когда они предлагают ответ. Чтобы заинтересовать всех, предложите награду за успешное прохождение игры, поощряя вызовы к подозрительным ответам.
***
Ищете учебную программу по математике, которая повысит уверенность учащихся в математике и предоставит вам богатые уроки и занятия для учащихся средней школы? Изучите HMH Into Math , наше основное математическое решение для классов K – 8.
Что такое длина? — Определение, факты и пример
Что такое длина?
Длина — это термин, используемый для определения размера объекта или расстояния от одной точки. Длина — это мера длины объекта или расстояния между двумя точками.Он используется для определения размера объекта или расстояния от одной точки до другой. Длина объекта — это его протяженное измерение, то есть его самая длинная сторона. Например, длина линейки на картинке 15 см.
Здесь стрелка над линейкой обозначает длину линейки, поскольку это самая длинная сторона линейки.
Еще несколько примеров:
Данное изображение представляет собой прямоугольник, и для каждого прямоугольника длина больше его ширины.
Инструмент для измерения длины
| Штангенциркуль | |
| Ленты |
Различная длина
Стандартная единица измерения длины в метрической системе — метр (м). В зависимости от длины, которую необходимо измерить, мы можем преобразовать метр в различные единицы, такие как миллиметры (мм), сантиметры (см) и километры (км).
Сантиметры и миллиметры помогают измерять меньшую длину, а метры и километры помогают измерять большую длину, например расстояние. Например, длину карандашей можно рассчитать в сантиметрах (см), а в километрах можно измерить расстояние между двумя зданиями или местами.
Сто равных делений метра дают сантиметр. Он пишется как «см». То есть
1 м = 100 см
Одна тысяча равных делений километра дает метр. То есть
1 км = 1000 м
Согласно таблицам преобразования длины, различные единицы длины и их эквиваленты приведены ниже:
Километр (км), метр (м) и сантиметр (см) — обычно используемые единицы длины.
Преобразование этих единиц осуществляется по указанной формуле.
Кроме того, в обычной системе (применяемой в США) в качестве единиц длины используются дюймы, футы, ярды и мили.
Соотношение между обычными единицами измерения приведено ниже:
Метрическая система и обычная система
С набором различных единиц метрическая система кажется вполне логичной системой по сравнению с обычной системой, а преобразование единиц в метрической системе намного проще, чем преобразование их в обычной системе.
Соединенные Штаты — последняя оставшаяся страна, которая еще не приняла метрическую систему. Однако с помощью данного преобразования легко преобразовать единицы из метрической системы в обычную.
1 метр (м) = 39,4 дюйма = 1,09 ярда;
1 ярд = 0,92 м
1 сантиметр (см) = 0,39 дюйма;
1 дюйм = 2,54 см
Интересные факты о длине
|
Общие математические символы и терминология
Математические символы и терминология могут сбивать с толку и мешать изучению и пониманию основ математики.
Эта страница дополняет наши страницы, посвященные навыкам счета, и предоставляет краткий глоссарий общих математических символов и терминологии с краткими определениями.
Мы что-то упускаем? Дайте нам знать.
Общие математические символы
+ сложение, плюс, положительное
Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.
Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2. Наша страница, посвященная положительным числам и отрицательным числам , объясняет, что число без знака считается положительным, поэтому плюс обычно не требуется.
Подробнее см. На нашей странице Дополнение .
— вычитание, минус, отрицательное значение
Этот символ имеет два основных применения в математике:
- — используется, когда нужно вычесть одно или несколько чисел, например, 2 — 2.
- Символ — также обычно используется для обозначения отрицательного или отрицательного числа, например −2.
Подробнее см. На нашей странице Вычитание .
× или * или. Умножение
Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.
Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.
Реже умножение также может быть обозначено точкой.или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) совпадает с 2 × (3 + 2).
См. Дополнительную информацию на нашей странице Умножение .
÷ или / Подразделение
Оба эти символа используются для обозначения деления в математике. ÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.
/ используется в электронных таблицах и других компьютерных приложениях.
Подробнее см. На нашей странице Division .
= равно
Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычислений, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.
Вы также можете встретить другие похожие символы, но они встречаются реже:
- ≠ означает не равно.Например, 2 + 2 ≠ 5 — 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
- ≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.
- ≈ означает приблизительно равно или почти равно. Две стороны отношения, обозначенные этим символом, будут , а не достаточно точными для математических манипуляций.
<Меньше и> Больше
Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.
Этот символ > означает больше, например, 4> 2.
≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре. В компьютерных приложениях используются <= и> =.
≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше.
± плюс или минус
Этот символ ± означает «плюс или минус». Он используется, например, для обозначения доверительных интервалов вокруг числа.
Говорят, что ответ — это «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.
Например, 5 ± 2 на практике может быть любым числом от 3 до 7.
∑ Сумма
Символ ∑ означает сумму.
∑ — заглавная греческая буква сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel — кнопка Автосумма имеет сигму в качестве значка.
° Градус
Градусы ° используются по-разному.
- В качестве меры поворота — угол между сторонами фигуры или поворот круга. Круг равен 360 °, а прямой угол — 90 °. См. Наш раздел о Геометрия для получения дополнительной информации.
- Мера температуры. градусов по Цельсию или по Цельсию используются в большинстве стран мира (за исключением США).Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется градус Фаренгейта. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F. Смотрите нашу страницу: Системы измерения для получения дополнительной информации.
∠ Угол
Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.
Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC может использоваться для описания угла точки A (между точками B и C).Подробнее об углах и других геометрических терминах см. На наших страницах Геометрия .
√ Квадратный корень
√ — символ квадратного корня. Квадратный корень — это число, которое при умножении на себя дает исходное число.
Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4. Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.
См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.
n Мощность
Целое число с верхним индексом (любое целое число n ) — это символ, используемый для обозначения степени числа.
Например, 3 2 означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).
4 3 означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.
См. Наши страницы Расчет площади и Расчет объема , где приведены примеры использования чисел в квадрате и кубе .
Степень также используется как сокращенный способ записи больших и малых чисел.
Большие числа
10 6 — 1 000 000 (один миллион).
10 9 — 1 000 000 000 (один миллиард).
10 12 — 1 000 000 000 000 (один триллион).
10 100 длинная рука будет равна 1 со 100 нулями (один гугол).
Маленькие числа
10 -3 — 0,001 (одна тысячная)
10 -6 равно 0.6 = 10 6 = 1000000 (один миллион).
. Десятичная точка
. — символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Decimals для примеров его использования.
, Разделитель тысяч
Запятую можно использовать для разделения больших чисел и облегчения их чтения.
Тысячу можно записать как 1000, так и 1000, а миллион — как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.
В большинстве англоязычных стран, не имеет математической функции, он просто используется для облегчения чтения чисел.
В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers .
[], () Скобки, круглые скобки
Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.
Части расчета, заключенные в скобки, вычисляются первыми, например
- 5 + 3 × 2 = 11
- (5 + 3) × 2 = 16
% В процентах
Символ% означает процент или число из 100.
Узнайте все о процентах на нашей странице: Введение в проценты
π Pi
π или пи — греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи — это длина окружности круга, деленная на ее диаметр, и имеет значение 3,141592653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.
∞ Бесконечность
Символ ∞ означает бесконечность — понятие, согласно которому числа существуют вечно.
Каким бы большим у вас ни было число, у вас всегда может быть номер побольше, потому что вы всегда можете добавить к нему еще один.
Бесконечность — это не число, а идея чисел, существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, полюбить или ненавидеть.
\ (\ bar x \) (x-bar) Среднее значение
\ (\ bar x \) — среднее всех возможных значений x.
Чаще всего этот символ встречается в статистике.
См. Нашу страницу Среднее значение для получения дополнительной информации.
! Факториал
! это символ факториала.
н! — произведение (умножение) всех чисел от n до 1 включительно, т.е. n × (n − 1) × (n − 2) ×… × 2 × 1.
Например:
5! = 5 × 4 × 3 × 2 × 1 = 120
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800
| Труба
Труба ‘|’ также называется вертикальной чертой, vbar, pike и имеет множество применений в математике, физике и вычислениях.
Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где \ (\ vert x \ vert \) — это абсолютное значение или модуль \ (x \) .
Математически это определяется как
$$ \ vert x \ vert = \ biggl \ {\ begin {eqnarray} -x, x \ lt 0 \\ x, x \ ge 0 \ end {eqnarray} $$
Проще говоря, \ (\ vert x \ vert \) — неотрицательное значение \ (x \). Например, модуль 6 равен 6, а модуль −6 также равен 6.
Он также используется в вероятности, где P (Z | Y) обозначает вероятность X при условии Y.
∝ Пропорциональный
∝ означает «пропорционально » и используется, чтобы показать что-то, что меняется по отношению к чему-то другому.
Например, если x = 2y, то x ∝ y.
∴ Следовательно
∴ — удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.
∵ Потому что
∵ — удобная сокращенная форма слова «потому что», не путать с «поэтому».
Математическая терминология (A-Z)
Амплитуда
Когда объект или точка движется циклически, или подвергается вибрации или колебаниям (например,грамм. маятник), амплитуда — это максимальное расстояние, на которое он перемещается от своей центральной точки. См. Введение в геометрию для получения дополнительной информации.
Апофема
Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.
Площадь
Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах ( 2 м).Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .
Асимптота
Асимптота — это прямая линия или ось, которая конкретно связана с изогнутой линией. По мере того, как кривая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Встречается в геометрии и тригонометрии .
Ось
Контрольная линия, вокруг которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.
Коэффициент
Коэффициент — это число или величина, умножающая другую величину. Обычно он помещается перед переменной . В выражении 6 x , 6 — коэффициент, а x — переменная.
Окружность
Окружность — это длина расстояния по краю круга. Это тип с периметром , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу, посвященную изогнутым формам .
Данные
Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественные или качественные переменные. Датум — это отдельное значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.
Диаметр
Диаметр — это термин, используемый в геометрии для определения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза превышает радиус .
Экстраполировать
Экстраполяция — это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого нет данных, с выводом значений неизвестных данных из тенденций в известных данных.
Фактор
Коэффициент — это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное количество факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два делителя — само себя и 1. Простой множитель — множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 — простые числа).
Среднее значение, медиана и мода
Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, среднее значение составляет . Режим — это число, которое встречается чаще всего.
Операция
Математическая операция — это шаг или этап в вычислении, или математическое «действие». Основные арифметические операции — сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок операций известен как BODMAS .
Математические операции часто называют «суммами». Строго говоря, «сумма» — это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи вы часто можете услышать общий термин «суммы», который неверен.
Периметр
Периметр двумерной фигуры — это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница по периметру объясняет это более подробно.
Пропорции
Пропорция — это относительное отношение. Соотношения сравнивают одну часть с другой, а пропорции сравнивают одну часть с целым. Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к дробям .
Пифагор
Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .
Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».
Количественный и качественный
Количественные данные — это числовые переменные или значения, которые могут быть выражены численно, то есть сколько, сколько, как часто, и получаются путем подсчета или измерения.
Качественные данные — это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.
Подробнее см. Нашу страницу о типах данных .
Радиан
Радиан — это единица СИ для измерения углов. Один радиан эквивалентен углу, образуемому в центре круга дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.
Радиус
Термин радиус используется в контексте кругов и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до ее внешнего края, поверхности или окружности . Диаметр вдвое больше радиуса. Для получения дополнительной информации см. Нашу страницу, посвященную изогнутым формам .
Диапазон
В статистике диапазон данного набора данных — это разница между наибольшим и наименьшим значениями.
Коэффициент
Коэффициент— это математический термин, используемый для сравнения размеров одной детали с другой.Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.
Стандартное отклонение
Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные распределены в более широком диапазоне
Срок
Термин — это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).
переменная
Переменная — это коэффициент , коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, который может изменяться.В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 — это коэффициент , , а x — переменная.
Разница
Дисперсия — это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе от среднего и, следовательно, от всех остальных членов в наборе.
Вектор
Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например. изучение движения, где скорость, ускорение, сила, смещение и импульс являются векторными величинами.
Объем
Объем — это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическими размерами пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м 3 .
Дополнительная литература по навыкам, которые вам нужны
Руководство по навыкам, которые вам нужны
Это руководство из четырех частей познакомит вас с основами математики от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрии и статистике.n $, множество слов длины $ n $ над $ A $. Пусть $ u = (u_1, \ ldots, u_n) $ и $ v = (v_1, \ ldots, v_n) $ — слова в $ C $. Расстояние Хэмминга $ d (u, v) $ определяется как количество мест, в которых $ u $ и $ v $ различаются: то есть $ \ sharp \ {i: u_i \ neq v_i, \, i = 1, \ точки, n \} $.
Расстояние Хэмминга удовлетворяет $$ d (u, v) \ ge 0 \ \ text {и} \ d (u, v) = 0 \ \ text {тогда и только тогда, когда} \ u = v \; $$ $$ d (u, v) = d (v, u) \; $$ $$ d (u, v) \ le d (u, w) + d (w, v) \. $$ Таким образом, расстояние Хэмминга является метрикой на $ C $.
В теории кодов с исправлением ошибок предполагается, что слова из $ C $ передаются по зашумленному каналу и что некоторые символы меняются во время передачи: см., Например, симметричный канал.Декодирование по методу максимального правдоподобия полученного слова $ r $ состоит в нахождении слова в $ C $, ближайшего к $ r $ в метрике Хэмминга. Если минимальное расстояние Хэмминга между словами $ C $ равно $ \ delta $, то этот процесс способен обнаруживать до $ \ delta-1 $ ошибок в $ r $ и исправлять до $ \ left \ lfloor \ frac { \ delta-1} {2} \ right \ rfloor $ ошибки.
Вес Хэмминга $ w (x) $ слова $ x $ над алфавитом, содержащим выделенный символ $ 0 $, — это расстояние $ d (\ mathbf {0}, x) $, где $ \ mathbf {0} $ — это слово, состоящее только из $ 0 $.Для линейных кодов в векторном пространстве над конечным полем расстояние определяется весом: $ d (x, y) = w (x-y) $.
Список литературы
- Goldie, Charles M .; Пинч, Ричард Г. Теория коммуникации , Студенческие тексты Лондонского математического общества.
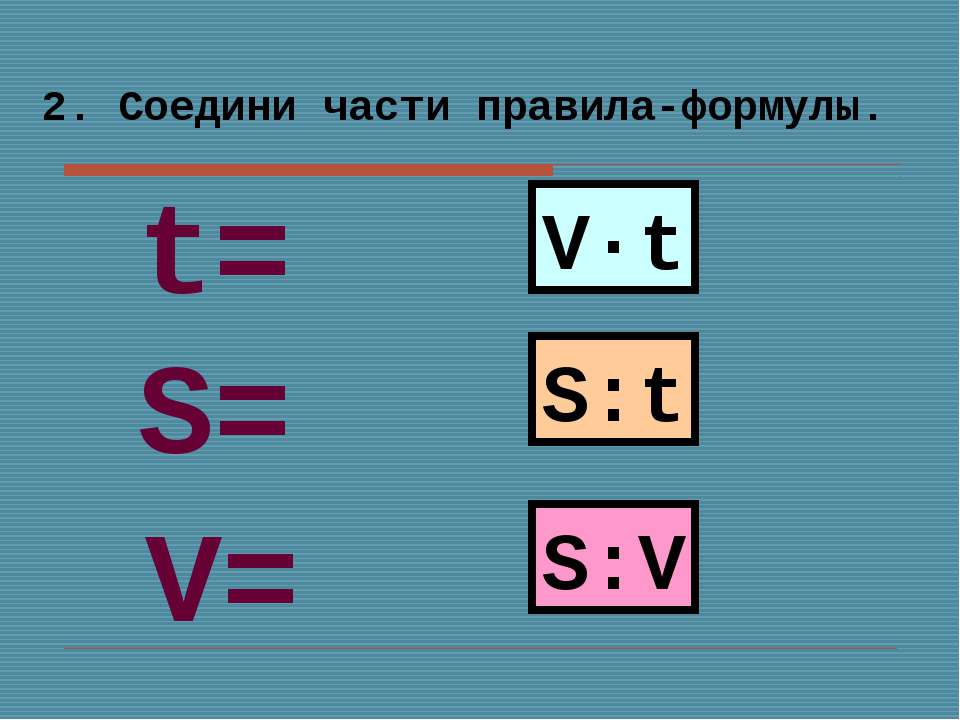
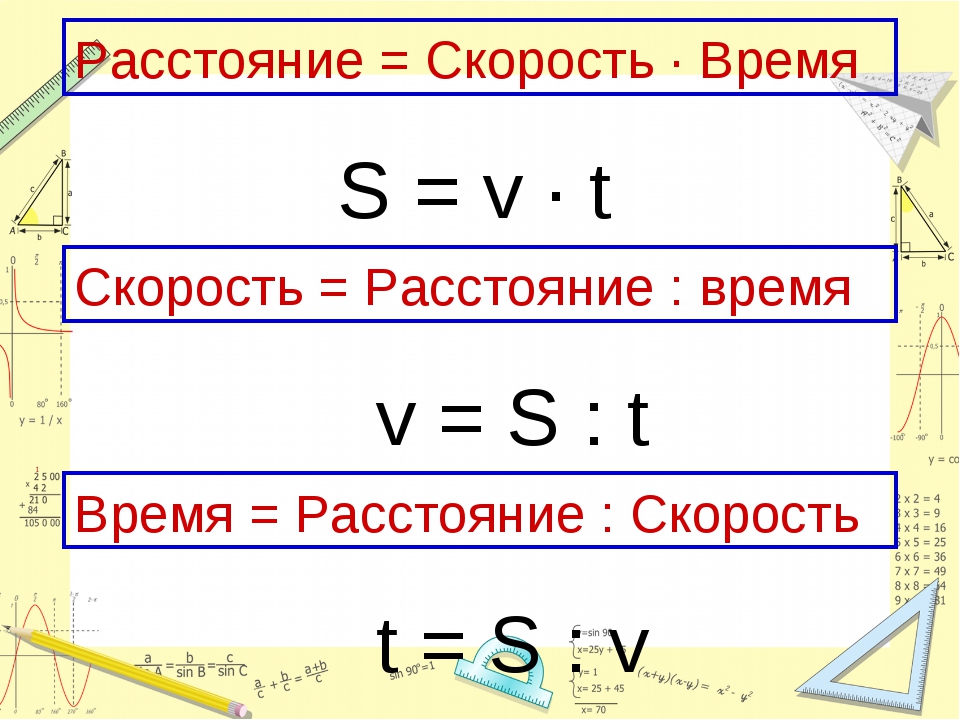

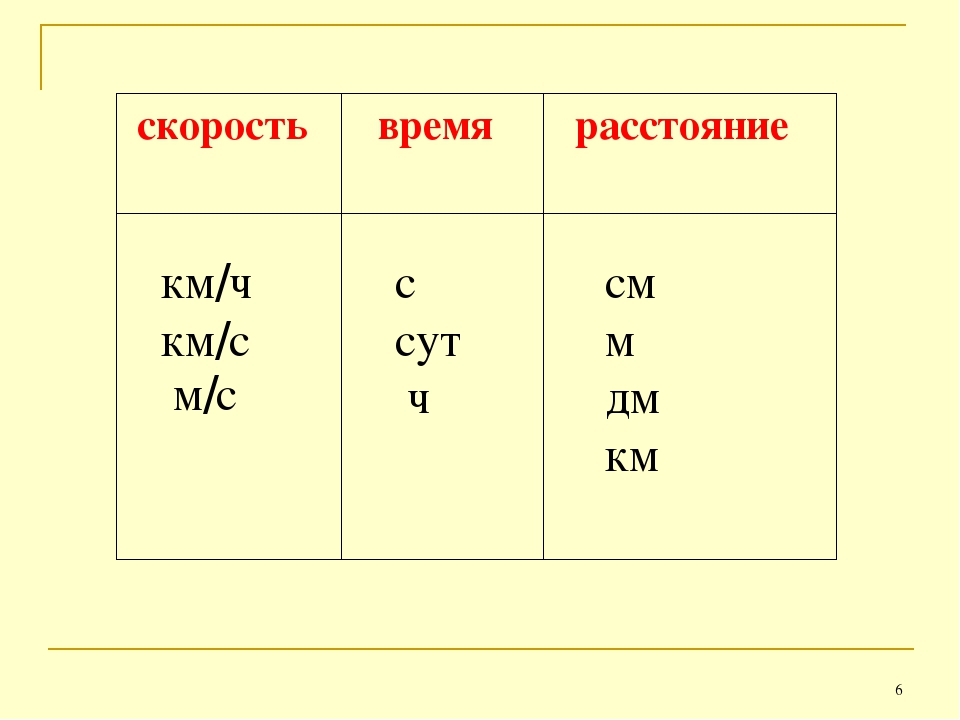

 А они появятся здесь, как только вы
назовёте эту передачу. Но слова зашифрованы. Что же делать?
А они появятся здесь, как только вы
назовёте эту передачу. Но слова зашифрованы. Что же делать?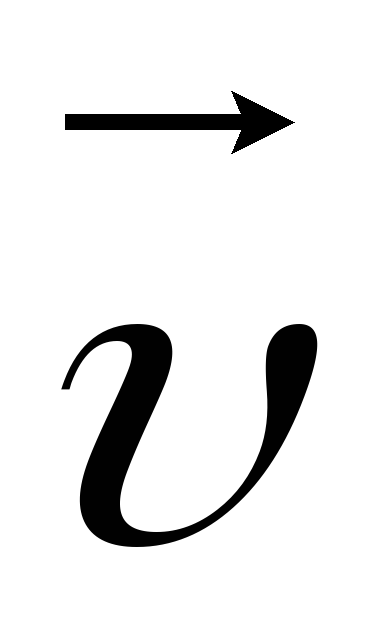



 Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц? Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?