Является ли линейная скорость постоянной величиной: является ли линейная скорость постоянной величиной при равнобедренном движении тела по
является ли линейная скорость постоянной величиной при равнобедренном движении тела по
3. Как изменится масса вещества, выделяющегося на электроде, если количество заряда, прошедшего через данный электролит, увеличить в 4 раза? А) не из … менится B) уменьшится в 2 раза С) увеличится в 2 раза D) увеличится в 4 раза E) уменьшится в 4 раза
25 БАЛЛОВ ВАШИ!!!!!! Полый цинковый шарик объёмом 9 см3 равномерно и прямолинейно поднимается вертикально вверх со дна стакана, заполненного нефтью. П … лотность цинка равна 7,1 г/см2, плотность нефти — 0,9 г/см2, плотность воздуха, заполняющего полость в шарике, равна 1,29 кг/м2. на картинке понятнее
Физика 11 класс 8 параграф решение
Жесткая рама расположенная вертикальной плоскости, закреплена в одной точке шарнирно неподвижной опоре, а в другой к невесомому стержню с шарнирами На
… раму действуют момент пары сил, сосредоточенная сила Р и распределенная нагрузка которых указаны в таблице. Определить реакции связей в точках А,В, вызываемые действующими нагрузками.
t=1s vo=0 S=0.5m m=25kg F=?
прихОманВариант 11. Вычислите импульс теламассой 12.6 кг , движущегося со скоростью 36 км /ч2. Найдите кинетическую энергию тела массой 0.45 кг ,движу … щегося со скоростью 10 км/с.3. Вычислите потенциальную энергию мяча, брошенного вертикально вверх, на высоте 3,5M, если его масса 350 гр.4. Железнодорожный вагон массой 60 т движется по прямолинейному участку пути соскоростью 1 км/ч. Какой станет скорость этого вагона после сцепки с неподвижнымвагоном массой 40 т?5. С неподвижной лодки, масса которой вместе с человеком 255 кг, бросают на берег весломассой 5 кг с горизонтальной скоростью относительно Земли, равной по модулю 10 м/с.Какую скорость приобретает лодка?6. Два тела одинакового объема, стальное и свинцовое, движутся с одинаковымискоростями. Сравните импульсы этих тел.
Максимальное значение напряженности электрического поля радиоволны не должно превышать Em=0,5 B/m. -7 Ф. Какова индуктивность катушки контура, если идет прием станции, работающей на длине волны 1000
… метров?
-7 Ф. Какова индуктивность катушки контура, если идет прием станции, работающей на длине волны 1000
… метров?
Урок 4. равномерное движение точки по окружности — Физика — 10 класс
Физика, 10 класс
Урок 04.Равномерное движение точки по окружности
Перечень вопросов, рассматриваемых на уроке:
- Равномерное движение точки по окружности и его характеристики.
- Центростремительное ускорение.
Глоссарий по теме
Криволинейное движение – это движение по дугам окружностей разных радиусов.
Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0
Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Ключевые слова
Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.
При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.
Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.
Векторы и не лежат на одной прямой, угол между ними не равен нулю.
Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.
Равномерное движение точки по окружности — это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение
Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение
Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.
Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.
Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была.
Модули скоростей равны:
но вектора скоростей не равны.
Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.
направлен в сторону.
Вспомним, что векторнаправлен по касательной, а касательная перпендикулярна радиусу окружности.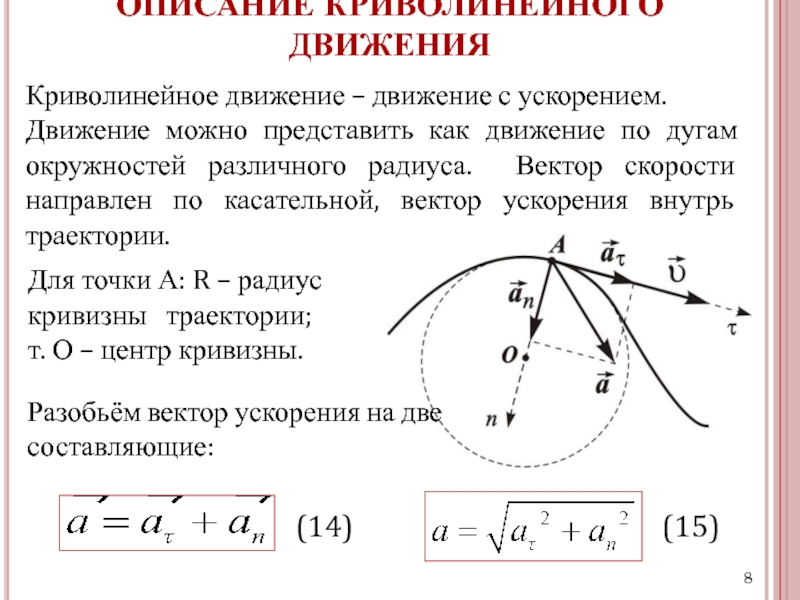 Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.
Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.
Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 900
Вектор будет перпендикулярен вектору в пределе
Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.
Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Длина дуги АВ это путь, пройденный точкой от А до В,
тогда запишем:
Умножим наи получим:
В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:
Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными
- Криволинейное движение — это движение по дугам окружностей разных радиусов.
А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.
Основные выводы:
— движение криволинейное, так как траекторией является окружность;
— движение равномерное, так как модуль скорости не меняется;
— вектор скорости направлен по касательной к окружности;
-вектор ускорения направлен к центру окружности;
— модуль центростремительного ускорения равен:
Примеры и разбор решения заданий
1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением
где R = 50 м; υ= км/ч = 10 м/с.
Тогда ac = (10 м/с)2 / 50 м = 2 м/с2.
Ответ: 2 м/с2
2. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Дано:
R1 =10см = 0,10 м
R2 = 30см = 0,30 м
Найти —
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением
Для тела 1 уравнение (1) примет вид:
для тела 2:
Тогда
Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.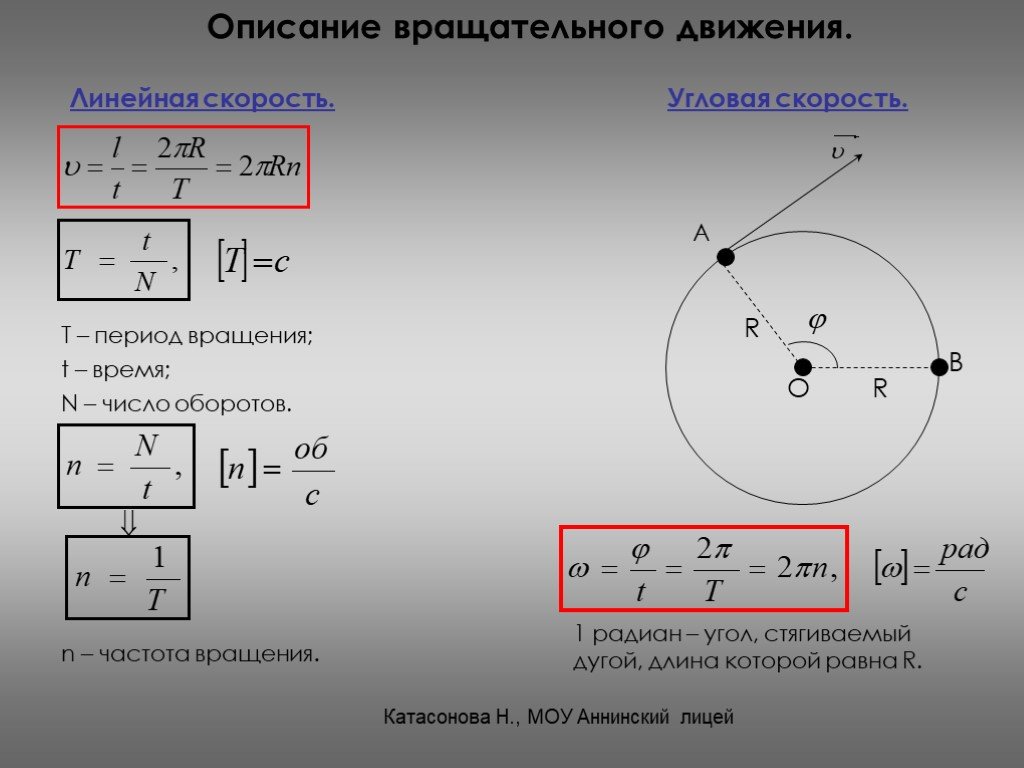
Выбор наилучшей линии тренда для ваших данных
Если вы хотите добавить линия тренда диаграмму в Microsoft Graph, вы можете выбрать любой из шести различных типов трендов и регрессий. Тип данных определяет тип линии тренда, который следует использовать.
Надежность линии тренда Линия тренда наиболее надежная, если ее величина достоверности аппроксимации находится вблизи 1. При подгоне линии тренда к данным Graph автоматически вычисляет значение величины R-квадрат. При этом вы можете отобразить это значение на диаграмме.
Линейная
Прямая линия тренда лучше всего подходит для простых линейных наборов данных. Данные линейно, если шаблон в точках данных напоминает линию. Иначе говоря, прямая линия тренда хорошо подходит для величины, которая возрастает или убывает с постоянной скоростью.
В следующем примере линейная линия тренда ясно показывает, что продажи продуктов компании постоянно растет в течение 13 лет. Обратите внимание, что величина квадрата R составляет 0,9036 , что хорошо подходит для данных.
Обратите внимание, что величина квадрата R составляет 0,9036 , что хорошо подходит для данных.
Логарифмическая
Логарифмическая линия тренда — это изогнутая линия, которая лучше всего подходит, когда скорость изменения данных быстро возрастает или уменьшается, а затем вырастет. Логарифмическая линия тренда может использовать отрицательные и (или) положительные значения.
В следующем примере логарифмическая линия тренда используется для демонстрации прогнозируемого роста популяции животных в области с фиксированным пространством, где население, выровненое по мере уменьшения пространства для животных, уменьшается. Обратите внимание, что величина квадрата R составляет 0,9407, что достаточно хорошо подходит для данных.
Полиномиальная
Полиномиальная линия тренда — это изогнутая линия, используемая при колебании данных. Это полезно, например, для анализа большого набора данных. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полиномиальная линия тренда no 2, как правило, имеет только один вершину или долину. По порядку 3 обычно один или два горы или долины. Как правило, у заказа 4 до трех.
Это полезно, например, для анализа большого набора данных. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полиномиальная линия тренда no 2, как правило, имеет только один вершину или долину. По порядку 3 обычно один или два горы или долины. Как правило, у заказа 4 до трех.
В следующем примере показана полиномиальная линия тренда второй показано (один вершина), чтобы показать связь между скоростью и расходом потребления. Обратите внимание, что величина квадрата R составляет 0,9474 , что хорошо подходит для данных.
Электропитание
Power trendline is a curved line that is best used with data sets that compare measurements that increase at a specific rate ( for the acceleration of a race car at one-second intervals. Если в данных имеются нулевые или отрицательные значения, использование степенной линии тренда невозможно.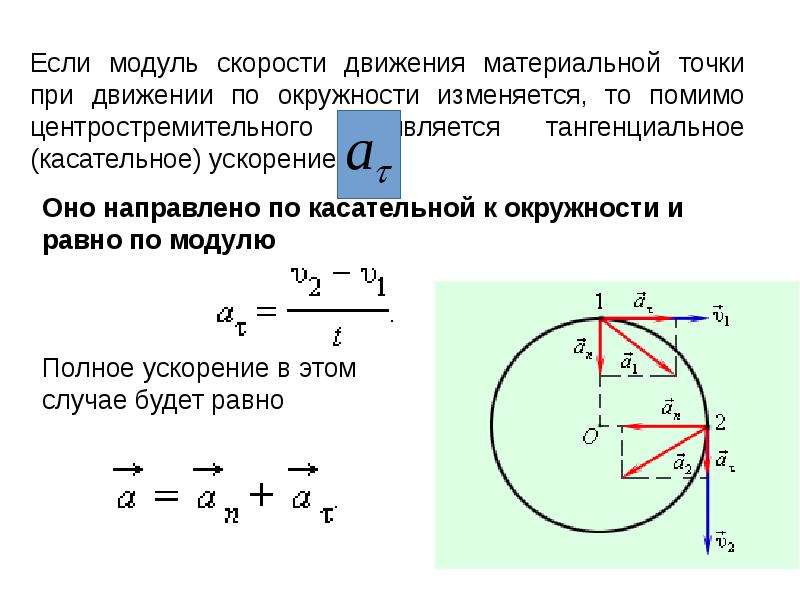
В следующем примере данные ускорения показаны путем отсекания расстояния в метрах за секунды. Расстояние выражено в метрах, время — в секундах. Величина квадрата R составляет 0,9923, что почти идеально подходит для данных.
Экспоненциальная
Экспоненциальной линией тренда является кривая линия, которая особенно полезна при увеличении или снижении значений данных. Однако для данных, которые содержат нулевые или отрицательные значения, экспоненциальная линия тренда неприменима.
В следующем примере экспоненциальное линия тренда используется для иллюстрации уменьшаемого объема 14 в объекте по мере возраста. Обратите внимание, что величина квадрата R составляет 1, что означает, что линия идеально подгощает данные.
Линейная фильтрация
Сглаживая линия тренда скользящего среднего сглаживает колебания данных, чтобы более четко показать тенденцию. При линии тренда скользящего среднего используется определенное количество точек данных (заданная с помощью параметра «Период»), среднее значение, а также среднее значение в качестве точки на линии тренда. Например, если значение «Период» имеет значение 2, то в качестве первой точки линии тренда скользящего среднего используется среднее значение первых двух точек данных. Среднее значение второй и третьей точек данных используется как вторая точка линии тренда и так далее.
При линии тренда скользящего среднего используется определенное количество точек данных (заданная с помощью параметра «Период»), среднее значение, а также среднее значение в качестве точки на линии тренда. Например, если значение «Период» имеет значение 2, то в качестве первой точки линии тренда скользящего среднего используется среднее значение первых двух точек данных. Среднее значение второй и третьей точек данных используется как вторая точка линии тренда и так далее.
В следующем примере линия тренда скользящего среднего отображает тенденцию в количестве домов, проданных в течение 26 недель.
Скорость линейная (окружная) — Энциклопедия по машиностроению XXL
При равномерном вращении кривошипа с постоянной угловой скоростью линейная окружная скорость в точке А пальца кривошипа определится вектором скорости приложенным в точке А перпендикулярно радиусу Величину окружной скорости можно определить исходя из количества двойных ходов кулисы п [c. 414]
414]Абсолютная, относительная, переносная, средняя, начальная, конечная, заданная, угловая, мгновенно угловая, постоянная, секторная, линейная, окружная, синхронная, возможная, виртуальная, обобщённая, первая (вторая) космическая, минимальная, максимальная, предельная, малая, номинальная, потерянная, круговая, параболическая. .. скорость. Адиабатическая, бесконечная. .. скорость звука. [c.83]
Установим зависимость между скоростью произвольной точки вращающегося тела и его угловой скоростью (применительно к вращающемуся телу вместо скорость точки часто I говорят линейная скорость или окружная [c.115]
Примером вращения, вызываемого силами сухого трения, является движение ременного приводного механизма. Ремень и ведомый шкив приводятся в движение силами трения, действующими между шкивами и надетым на них ремнем. При этом нормально ремень и шкивы движутся так, что линейные скорости на окружности шкива и внутренней поверхности ремня одинаковы. Поэтому не происходит тангенциальных
[c.201]
Поэтому не происходит тангенциальных
[c.201]
Спин является квантовой величиной, не имеющей классического аналога. Однако некоторую связь спина с классическими образами можно проследить. Представим электрон окружностью радиуса г, по которой равномерно распределена масса с линейной плотностью mj 2nr). Направим ось вращения электрона перпендикулярно плоскости окружности через ее центр и обозначим V линейную скорость точек окружности при вращении. Момент импульса электрона с учетом релятивистского изменения массы равен г vj — v j . Скорость v с учетом (34.3) определяется из уравнения [c.203]
Рассмотрим наиболее простой случай, когда передаче устанавливается между двумя параллельными валами при помощи гладких цилиндрических колес / и 2 (рис. 185). Эти колеса закреплены на ведущем валу 0 и на ведомом При достаточном нажатии колес движение происходит без скольжения и, следовательно, линейные окружные скорости их или, так как
[c. 163]
163]
В процессе расчета принимают значения ряда параметров и определяют окружные скорости, линейную нагрузку, напряжения, деформации и т. д. При этом в соответствии с [14, 26] могут быть даны следующие рекомендации. [c.302]
Поэтому, обозначив через г и радиусы шкивов С, и через ш и угловые скорости установившегося движения (соответственно вокруг О и Oi), мы получим, приравнивая линейные окружные скорости, [c.309]
Определение условного радиуса траектории и ножей. При основном расчётном числе оборотов ножей п горизонтальная проекция линейной окружной скорости ножей в момент начала резания нг должна быть меньше скорости подачи полосы 1>о, так как в противном случае полоса в период реза будет изгибаться, а по окончании реза может быть затянута ножом вокруг барабана, что поведёт к аварии ножниц (фиг. 50) [c.981]
Параметры и результаты закалки. Основными параметрами поверхностной закалки при контактном электронагреве являются а) сила тока во вторичной цепи или плотность тока на 1 пог. им ширины ролика б) скорость обработки (окружная скорость для тел вращения и линейная для плоскостей) в) давление
[c.181]
им ширины ролика б) скорость обработки (окружная скорость для тел вращения и линейная для плоскостей) в) давление
[c.181]
Вращение вала электродвигателя при помощи пары конических шестерен передается валику 1, в котором эксцентрично закреплен палец 2 с посаженным на него роликом 3. Ролик служит для уменьшения трения пальца о ведомую им деталь. Ведущий палец вместе с роликом входит в фигурную прорезь, имеющуюся в ударнике 4. При движении ведущего пальца по описываемой им окружности он заставляет ударник совершать возвратно-поступательное движение. Конфигурация прорези такова, что при рабочем ходе скорость ударника возрастает от нуля до скорости, равной линейной скорости на окружности с радиусом, определенным расстоянием от центра валика I до внешней поверхности ролика 3. [c.423]
При работе ротора усилие резания складывается из двух составляющих окружного усилия на роторе, создаваемого приводом ротора, и усилия, которое возникает при движении ротора вдоль трассы, т. е. от его продольной подачи. Чем выше скорость линейного движения, тем больше глубина врезания ковша в грунт и тем больше коэффициент заполнения ковша. Большую роль в этом играет умение машиниста правильно выбрать режимы работы ротора и режимы рабочего хода экскаватора. От их правильного сочетания зависит производительность экскаватора и до некоторой степени его надежность и долговечность.
[c.92]
е. от его продольной подачи. Чем выше скорость линейного движения, тем больше глубина врезания ковша в грунт и тем больше коэффициент заполнения ковша. Большую роль в этом играет умение машиниста правильно выбрать режимы работы ротора и режимы рабочего хода экскаватора. От их правильного сочетания зависит производительность экскаватора и до некоторой степени его надежность и долговечность.
[c.92]
Понятие о движении (прямолинейном и криволинейном, равномерном и неравномерном), Понятие о линейной, окружной и угловой скорости. Понятие об инерции и силе. Сила трения. Центробежная и центростремительная сила. Деформация тел (упругие и остающиеся деформации). [c.612]
Ущг — колебание длины общей нормали, мкм о — окружное перемещение, мм скорость линейная, м/с Рвл— скорость линейная т. В относительно т. А, м/с W, А — работа, Дж, кДж, МДж, кВт-ч [c.6]
I. Пусть стационарное осесимметричное (ось симметрии жз) движение вязкой жидкости с Т = О, описываемое уравнениями Навье-Стокса, имеет поле скоростей, линейное по жз. Вводя радиальную окружную икомпоненты вектора скорости и полагая
[c.185]
Вводя радиальную окружную икомпоненты вектора скорости и полагая
[c.185]
Линейная скорость по окружности шестерни при числе оборотов = 715 об мин [c.85]
Линейная скорость на окружности шестерни [c.137]
Линейная скорость по окружности среднего диаметра шестерни (рис. 63) [c.212]
Величина угла у обычно принимается в пределах 60—120°. Линейная скорость на окружности колеса [c.239]
При полировании различных металлов круг должен иметь определенные окружные скорости (табл. 5). Число оборотов круга при заданной линейной (окружной) скорости вращения определяется его диаметром. [c.27]
Очень удобно в этом случае применить метод планов скоростей. Так как линейные окружные скорости на поверхности цилиндра одинаковы для всех точек, то для примера скорости точек М и Я могут быть представлены равновеликими векторами V, отложенными по вертикальному направлению. Проектируя эти скорости на нормали а и 6, получим в горизонтальном направлении векторы скоростей точек М и Я, обозначенные через v на седьмой горизонтали и v на четвертой. Подобным же образом могут быть построены ( векторы скоростей и для других мо- ] ментов движения. [c.357]
V — окружное перемещение, мм скорость линейная, м/с [c.6]
Линейную (окружную) скорость точки вращающегося тела (м/с) определяют по формуле [c.22]
Задача 5. Для конической фрикционной передачи, геометрические оси которой пересекаются под прямом углом, вычислить передаточное отношение, угловую скорость ведомого вала, линейную скорость на окружности средних диаметров катков, средние диаметры катков, их ширину и конусное расстояние, если [c.37]
Вычисляем линейную скорость на окружности средних диаметров катков [c.37]
Линейная (окружная) скорость v — a>R R — радиус окружности вращения. [c.25]
В этом случае груз катится по роликам без скольжения, т. е. движется с линейной скоростью, равной окружной скорости роликов, и его масса участвует в действующих на роликовом конвейере динамических силах. [c.408]
Отсутствие водоворотов. Линейный интеграл от скорости по окружности воронки водоворота не равен нулю. В бесконечно малом масштабе наличие маленьких завихрений приведет к тому (закон Стокса), что ротор от вектора v не будет равен нулю. (Чтобы вспомнить понятие ротора вектора, см. т. II, пп. 2.15—2.18.) Мы предполагаем, что завихрений нет, т. е. [c.313]
Поверочный расчет колес второй передачи на изгиб. Линейная скорость на окружности шестерни [c.86]
Линейная скорость на окружности среднего диаметра шестерни [c.196]
Несущая способность конических колес с линейным контактом зависит от неточностей монтажа в большей мере, чем передач с цилиндрическими зубчатыми колесами. Поэтому при одинаковых окружных скоростях для конических колес назначается точность на степень выше, чем для цилиндрических (см. табл. 6.7). [c.124]
Заметим, что при сближении точечных вихрей их скорости неограниченно растут, поэтому при практической реализации метода применяют те или иные способы регуляризации. В книге С.М. Белоцерковского и М.И. Ништа [1978J предлагается вводить некоторый радиус усечения 5. При сближении вихрей на расстояние менее 5 на индуцированные скорости накладывается ограничение скорость внутри окружности радиуса 5 определяется линейной интерполяцией между значением скорости на окружности и нулевым значением скорости па оси вихря. В работе одного из основателей вихревых методов — Rosenhead [1930] — применялась простая алгебраическая регуляризация, заключающаяся в замене знаменателей в уравнениях (6.1) на величину а — + 5. Более полный перечень приемов регуляризации можно найти в обзоре Leonard [1980]. Таким образом, фактически вместо точечных вихрей используются объекты конечных размеров — вихревые частицы. [c.321]
При универсальной электроизмерительной части расходомера основные метрологические и эксплуатационные свойства прибора определяются особенностями первичных преобразователей. Конструктивно скоростные тахометрические преобразователи выполняются либо с роторами в виде осевых или тангенциальных миниатюрных крыльчатых турбинок, либо со свободно вращающимися шариками (рис. 148). Прямолопастные осевые турбинки и шарики приводятся в движение с помощью предварительной закрутки потока в тангенциальных камерах или на неподвижных винтовых шнеках. Встречаются конструкции (обычно малых калибров), в которых создается предварительная закрутка потока [29]. В тангенциальных турбинных преобразователях ротор вращается вокруг оси, перекрещивающейся с осью потока лопасти турбинки выполняются в виде пластин или чашечек. Поток жидкости поступает на лопасти ротора через направляющий аппарат — одноструйный или многоструйный первый предпочтительнее при малых диаметрах трубопровода, второй — при средних и больших. В шариковых тахометрических преобразователях увлекаемый закрученным потоком жидкости шарик движется со скоростью, пропорциональной окружной скорости потока и, следовательно, его объемному расходу. Центробежные силы удерживают шарик на периферии камеры преобразователя и препятствуют уносу его потоком. Шариковые преобразователи уступают крыльчатым в точности [погрешность порядка (1,5—2,0)% ], имеют повышенные гидравлические потери и узкий диапазон линейности статической характеристики, но зато работоспособны при значительных загрязнениях потока. [c.352]
Линейная окружная скорость V (м/с) определяется по формуле г = п0п160, где О — диаметр окружности точки вращения, м. [c.140]
Допустим, что наружное и внутреннее кольца подшипника совершают соответственно и Пв об1мин. Будем считать вращение положительным, если оно направлено по часовой стрелке, и отрицательным, если оно направлено против часовой стрелки. Пусть и — линейные скорости точек окружностей С и С . Тогда линейная скорость центра шарика равна [c.40]
Вращение вала электродвигателя при помощи пары конических щестерен передается валику 13, в котором эксцентрично закреплен ведущий палец 4, снабженный роликом 5. Ролик 5 служит для уменьшения трения пальца о ведомую деталь. Ведущий палец вместе с роликом входит в фигурную прорезь, имеющуюся в ударнике 6. При движении ведущего пальца по окружности он заставляет ударник совершать возвратно-поступательное движение. Конфигурация прорези ударника такова, что при рабочем ходе скорость ударника возрастает от нуля до скорости, равной линейной скорости на окружности с радиусом, определяемым расстоянием от центра валика 13 до внешней поверхности ролика 5. При достижении этой максимальной скорости происходит отрыв ударника от ролика или, иначе говоря, свободный бросок ударника, который производит удар по бойку 2, после чего ролик отводит ударник назад для нового рабочего хода. Одному обороту ведущего пальца соответствует один рабочий ход ударника. При включении электродвигателя, пока отсутствует нажнм на рабочий инструмент, ударник не достигает бойка 2 и своими боковыми заплечиками производит удары по направляющей втулке 3. Эти удары амортизируются сильной пружиной I, которая прижимает направляющую втулку к корпусу. При нажиме на инструмент последний своим хвостовиком сближает боек 2 с ударником, и электромолоток переходиг на рабочий режим. [c.144]
Скорость у движения по окружности называется линейной (окружной) скоростью. При равномерном движении по окружности модуль V мгновенной скорости материальной точки (1.1.3.2°) с течением времени не изменяется о=сопз1 (Ул= й= с на рис. 1.1.21). Движуш,аяся точка за равные промежутки времени проходит равные по длине дуги окружности. [c.30]
Перемещение приемников давления по координатам i и г осуществлялось дискретно, по координате (р — непрерывно в пределах изменения полярного угла 9 от О до 360°. Азимутальный координатник обеспечивал перемещение пневмоприемников по окружности соосной соплу (г = onst) с линейной скоростью на окружности, равной 0,2 мм/с. Точность установки пневмоприемника по координате г для данной серии измерений составляла 0,05 мм. [c.166]
Мёллер [1048] описывает установки с неполным погружением, которые при диаметре трубы до 160 мм являются изящным решением транспортировки трубы по спирали ванна с искателями располагается между двумя устройствами для вращательной подачи. В ванне вращаются тройные ролики, предназначенные для чисто продольной транспортировки трубы, так что частоту вращения и скорость линейной транспортировки трубы можно устанавливать независимо друг от друга. Таким путем можно бесступенчато получить любой подъем спирали контроля — от чистого вращения до чисто линейной транспортировки. Кроме того, при такой схеме транспортировки можно легко снимать координаты по окружности и по длине ввода в расшифровывающее устройство, в предположении, что проскальзывание между трубой и системой привода может быть исклю-[c.500]
При этом точка отрыва смещается по ходу потока (рис. 5-5). При вращении шара дополнительное значение имеет взаимонаправле-ние окружной и линейной скорости, а также интенси- [c.156]
формула, единица измерения, как рассчитать через обороты в минуту и радиус
Что такое линейная скорость, единицы измерения
ОпределениеСкоростью при равномерном движении тела называют физическую величину, с помощью которой определяют путь, преодоленный телом за единицу времени.
В международной системе СИ единицей измерения линейной скорости является производная от двух основных единиц:
- метр;
- секунда.
В международной системе СИ скорость измеряется в метрах в секунду (м/с). За единицу скорости принимают скорость равномерного движения, при которой путь в один метр тело преодолеет в течение одной секунды. Кроме того, скорость можно измерять в:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- км/ч;
- км/с;
- см/с.
Связь между линейной и угловой скоростями
Скорость точки, которая совершает круговое движение, называется линейной скоростью, чтобы отделить это понятие от термина угловая скорость. Во время вращения абсолютно твердое тело в разных точках будет обладать неодинаковыми линейными скоростями, но значение угловой скорости остается стабильным.
Источник: class-fizika.ruМожно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет:
2πR
Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:
\(v=\frac{2\pi R}{T}=2\pi RV\)
Зная, что:
\(\omega =2\pi V\)
получим справедливое равенство:
\(v=\omega R\)
Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения.{2}R\)
Таким образом, рассматривают пару простейших движений, характерных для абсолютно твердого тела, включая поступательное и вращательное. При этом стоит отметить, что определить любое сложное движение, которое совершает абсолютно твердое тело, можно с помощью суммы двух независимых движений:
- поступательное;
- вращательное.
С помощью закона независимости движений описывают сложное движение абсолютно твердого тела.
Формулы для нахождения линейной скорости
Тело движется равномерно тогда, когда его скорость характеризуется постоянной величиной. Формула для расчета скорости такого движения будет иметь следующий вид:
V = st
где s является пройденным путем, то есть длиной линии;
t представляет собой время, в течение которого тело преодолевало указанный путь.
ОпределениеЛинейной скоростью V называют физическую величину, которая демонстрирует путь, пройденный телом в течение определенного времени.
Основной формулой для определения линейной скорости является следующее равенство:
V = St
где S является путем,
t обозначает время, в течение которого тело преодолело путь S.
Иной вариант уравнения имеет такой вид:
V = lt
где l является путем,
t обозначает время, в течение которого тело преодолело дугу l.
В некоторых научных источниках скорость обозначают с помощью маленькой буквы v. Другим уравнением для расчета линейной скорости является равенство:
\(v=2\pi RT\)
В данном случае 2π представляет собой полную окружность и составляет 360 угловых градусов. Вектор скорости направлен по касательной к траектории движении тела.
Модуль скорости
Числовое значение скорости может быть разным в зависимости от выбранной единицы измерения. Кроме числового значения, скорость характеризуется направлением. Числовое значение, которым обладает скорость, в физике называют ее модулем.{2}}{R}\)
\(v=\sqrt{aR}=\sqrt{40\times 3}=10.9\) м/с
Ответ: линейная скорость равна 10,9 м/с.
Задача №2
Поезд совершает равномерное движение. В течение 4 часов он преодолевает путь в 219 километров. Требуется рассчитать скорость движения поезда.
Решение:
Исходя из основной формулы для расчета линейной скорости, получим:
\(v=\frac{S}{t}=\frac{219}{4}=54.75\) км/ч
Ответ: скорость движения поезда составит 54.75 км/ч или 15.2 м/с.
Задача №3
Транспортное средство, работая на двигателе внутреннего сгорания, в течение 2,5 часов преодолевает расстояние в 213 километров. Требуется определить скорость движения транспорта.
Решение:
С помощью уравнения расчета скорости можно записать решение задачи:
\(v=\frac{S}{t}=\frac{213}{2,5}=85.2\) км/ч
Ответ: Скорость движение транспортного средства составляет 85.2 км/ч или 23.7 м/с.
Определение CLV (постоянной линейной скорости)
Название компании Страна UNITED STATESUNITED KINGDOMCANADAAUSTRALIAINDIA —— AfghanistanÅland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua и BarbudaArgentinaArmeniaArubaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Синт-Эстатиус и SabaBosnia и HerzegovinaBotswanaBouvet IslandBrazilBritish Индийский океан TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCambodiaCameroonCape VerdeCayman IslandsCentral африканских RepublicChadChileChinaChristmas IslandCocos (Килинг) IslandsColombiaComorosCongoCongo, Демократическая Республика theCook IslandsCosta RicaCôte D’IvoireCroatiaCubaCuraçaoCuraçaoCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial ГвинеяЭритреяЭстонияЭфиопияФолклендские острова (Мальвинские острова) Фарерские островаФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияФранцузские Южные территорииГабонГамбияГрузияГерманияГанаГибралтарствоГрецияГренландияГренадаГваделупа-ГуамГватемалаГернаГерна Биссау, Гайана, Гаити, Херд, острова Макдональд.HondurasHong KongHungaryIcelandIndonesiaIran, Исламская Республика ofIraqIrelandIsle из ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKorea, Корейская Народно-Демократическая Республика ofKorea, Республика ofKuwaitKyrgyzstanLao Народная Демократическая RepublicLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacaoMacedonia, бывшая югославская Республика ofMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesia, Федеративные Штаты ofMoldova, Республика ofMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNetherlands AntillesNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorthern Mariana IslandsNorwayOmanPakistanPalauPalestine, Государственный ofPanamaPapua Новый GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRéunionRomaniaRussian FederationRwandaSaint BarthélemySaint Елены, Вознесения и Тристан-да-Кунья, Сент-Китс и Невис, Сент-Люсия, Сен-Мартен (Французская часть), Сен-Пьер и MiquelonSaint Винсент и GrenadinesSamoaSan MarinoSao Томе и PrincipeSaudi ArabiaSenegalSerbiaSerbia и MontenegroSeychellesSierra LeoneSingaporeSint Маартен (Голландская часть) SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Джорджия и Южные Сандвичевы IslandsSouth SudanSpainSri LankaSudanSurinameSvalbard и Ян MayenSwazilandSwedenSwitzerlandSyrian Arab RepublicTaiwanTajikistanTanzania, Объединенная Республика ofThailandTimor-LesteTogoTokelauTongaTrinidad и TobagoTunisiaTurkeyTurkmenistanTurks и Кайкос IslandsTuvaluUgandaUkraineUnited Арабские EmiratesUnited Штаты Экваторияльная Острова УругвайУзбекистан ВануатуВатикан Венесуэла, Боливарианская Республика Вьетнам Виргинские острова, Британские Виргинские острова, СШАС.Уоллис и Футуна, Западная Сахара, Йемен, Замбия, Зимбабве.
Скорость и скорость
Любой движущийся объект можно описать с помощью кинематических концепций, обсуждаемых в Блоке 1 Физического Класса. Движение движущегося объекта может быть объяснено либо с помощью законов Ньютона (блок 2 в классе физики) и векторных принципов (блок 3 в классе физики), либо с помощью теоремы работы-энергии (блок 5 в классе физики).Те же концепции и принципы, которые используются для описания и объяснения движения объекта, могут быть использованы для описания и объяснения параболического движения снаряда. В этом модуле мы увидим, что те же самые концепции и принципы могут также использоваться для описания и объяснения движения объектов, которые либо движутся по кругу, либо могут быть аппроксимированы движущимися по кругу. Кинематические концепции и принципы движения будут применены к движению объектов по кругу, а затем будут расширены для анализа движения таких объектов, как американские горки, футболист, совершающий круговой поворот , и планета, вращающаяся вокруг Солнца.Мы увидим, что красота и сила физики заключаются в том, что несколько простых концепций и принципов могут быть использованы для объяснения механики всей Вселенной. Урок 1 этого исследования начнется с разработки кинематических и динамических идей, которые можно использовать для описания и объяснения движения объектов по кругу.
Предположим, что вы управляете автомобилем с повернутым рулевым колесом таким образом, что ваш автомобиль движется по идеальному кругу с постоянным радиусом.Предположим, что во время движения ваш спидометр постоянно показывает 10 миль в час. В такой ситуации движение вашего автомобиля можно описать как равномерное круговое движение. Равномерное круговое движение — это движение объекта по кругу с постоянной или равномерной скоростью.
Расчет средней скоростиРавномерное круговое движение — круговое движение с постоянной скоростью — это одна из многих форм кругового движения.Объект, движущийся равномерно по кругу, преодолеет такое же линейное расстояние за каждую секунду. При движении по кругу объект проходит расстояние по периметру круга. Итак, если ваша машина будет двигаться по кругу с постоянной скоростью 5 м / с, то машина будет проходить 5 метров по периметру круга за каждую секунду. Расстояние одного полного цикла по периметру круга известно как окружность . С постоянной скоростью 5 м / с автомобиль мог совершить полный цикл по кругу с окружностью 5 метров.При этой равномерной скорости 5 м / с каждый цикл по окружности длиной 5 м потребует 1 секунды. На скорости 5 м / с круг с окружностью 20 метров можно было сделать за 4 секунды; и при этой равномерной скорости каждый цикл по 20-метровой окружности круга будет занимать один и тот же период времени в 4 секунды. Эта взаимосвязь между длиной окружности, временем завершения одного цикла по кругу и скоростью объекта является просто расширением уравнения средней скорости, изложенного в Блоке 1 Физического Класса.
Окружность любого круга может быть вычислена, используя радиус в соответствии с уравнением
Окружность = 2 * Пи * РадиусОбъединение этих двух приведенных выше уравнений приведет к новому уравнению, связывающему скорость объекта, движущегося в равномерном круговом движении, с радиусом круга и временем, чтобы сделать один цикл по кругу (период , ).
, где R представляет радиус окружности, а T представляет период.Это уравнение, как и все уравнения, можно использовать как алгебраический рецепт для решения проблемы. Его также можно использовать, чтобы направлять наши размышления о том, как переменные в уравнении связаны друг с другом. Например, уравнение предполагает, что для объектов, движущихся по кругам разного радиуса за один и тот же период, объект, пересекающий круг большего радиуса, должен двигаться с наибольшей скоростью. Фактически, средняя скорость и радиус круга прямо пропорциональны. Двукратное увеличение радиуса соответствует двукратному увеличению скорости; трехкратное увеличение радиуса соответствует трехкратному увеличению скорости; и так далее.Чтобы проиллюстрировать это, рассмотрим цепочку из четырех светодиодных ламп, расположенных в разных местах вдоль жилы. Прядь держится за один конец и быстро скручивается по кругу. Каждый светодиодный светильник проходит по кругу разного радиуса. Тем не менее, поскольку они подключены к одному проводу, период их вращения одинаков. Впоследствии светодиоды, которые находятся дальше от центра круга, перемещаются быстрее, чтобы охватить окружность большего круга за то же время. Если освещение комнаты выключено, светодиоды создают дугу, которая может казаться более длинной для тех светодиодов, которые перемещаются быстрее — светодиодов с наибольшим радиусом.Это показано на диаграмме справа.
Направление вектора скорости
Объекты, движущиеся равномерно по кругу, будут иметь постоянную скорость. Но означает ли это, что они будут иметь постоянную скорость? Вспомните из раздела 1 «Класса физики», что скорость и скорость относятся к двум совершенно разным величинам. Скорость — это скалярная величина, а скорость — это векторная величина.Скорость, будучи вектором, имеет как величину, так и направление. Величина вектора скорости — это мгновенная скорость объекта. Направление вектора скорости направлено в том же направлении, что и объект. Поскольку объект движется по кругу, его направление постоянно меняется. В какой-то момент объект движется на север так, что вектор скорости направлен на север. Четверть цикла спустя объект будет двигаться на восток, так что вектор скорости будет направлен на восток.Поскольку объект огибает круг, направление вектора скорости отличается от того, что было в предыдущий момент. Таким образом, хотя величина вектора скорости может быть постоянной, направление вектора скорости меняется. Лучшее слово, которое можно использовать для описания направления вектора скорости, — это слово тангенциальный . Направление вектора скорости в любой момент находится в направлении касательной линии, проведенной к окружности в месте расположения объекта. (Касательная линия — это линия, которая касается окружности в одной точке, но не пересекает ее.На диаграмме справа показано направление вектора скорости в четырех разных точках для объекта, движущегося по часовой стрелке по окружности. В то время как фактическое направление объекта (и, следовательно, вектора скорости) изменяется, его направление всегда касается окружности.
Подводя итог, объект, движущийся равномерно по кругу, движется по периметру круга с постоянной скоростью. Пока скорость объекта постоянна, его скорость меняется.Скорость, будучи вектором, имеет постоянную величину, но меняющееся направление. Направление всегда направлено касательно окружности, и когда объект поворачивает круг, касательная линия всегда указывает в новом направлении.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства Uniform Circular Motion Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать векторы скорости, ускорения и силы для объекта, движущегося по кругу.
1. На стол кладут трубку, придающую ей форму круга в три четверти.Мяч для гольфа проталкивается в трубку одним концом на высокой скорости. Мяч катится по трубке и выходит на противоположном конце. Опишите путь мяча для гольфа, когда он выходит из трубы.
Линейное перемещение
Переход к делу
Обсуждение
Эти уравнения движения действительны только при постоянном ускорении и ограничении движения прямой линией.В реальном мире это нереалистичное представление. Ни один объект никогда не двигался по прямой с постоянным ускорением где-либо во Вселенной в любое время. Однако было бы неправильно отбрасывать этот раздел сразу или как бесполезный.
Во многих случаях полезно предположить, что объект двигался или будет двигаться по пути, который по существу прямой и с почти постоянным ускорением. То есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории также может быть одномерным. если для задействованных объектов существует только одна степень свободы.Например, дорога может извиваться и поворачиваться и исследовать все виды направлений, но автомобили, движущиеся по нему, имеют только одну степень свобода: свобода двигаться в одном или противоположном направлении направление. (Вы не можете ездить по дороге по диагонали и надеетесь остаться на нем очень долго.) В этом отношении он мало чем отличается от движения с ограничением к прямой. Аппроксимация реальных ситуаций с помощью моделей на основе в идеальных ситуациях не считается обманом. Это способ вещей покончить с физикой.Это такой полезный метод, который мы будем использовать это снова и снова.
Наша цель в этом разделе — вывести уравнения, которые можно использовать для описывать движение объекта с точки зрения его трех кинематических переменные: скорость, перемещение и время. Есть три способа объединить их в пары: скорость-время, смещение-время и скорость-смещение. В этом порядке их также часто называют первым, вторым и третье уравнение движения, но нет веских причин изучать эти имена.Поскольку мы имеем дело с движением по прямой, символ x будет использоваться для смещения. Направление движения будет обозначено знаком (положительный величины указывают в направлении + x, в то время как отрицательные величины указывают в направлении -x). Определение того, какое направление является положительным и что отрицательное совершенно произвольно. Законы физики изотропны; то есть они не зависят от ориентации системы координат. Пока вы последовательны, это не имеет значения.Некоторые проблемы однако легче понять и решить, когда выбрано одно направление положительный по сравнению с другим.
Скорость-время
Связь между скоростью и временем проста при постоянном ускоренное, прямолинейное движение. Постоянное ускорение подразумевает равномерная скорость изменения скорости. Чем дольше разгон, тем больше изменение скорости. Если по прошествии времени скорость увеличивается на определенную величину, по прошествии двух раз она должна увеличиться на вдвое больше.Изменение скорости прямо пропорционально времени , когда ускорение постоянное. Если объект уже запущен с определенным скорости, тогда его новая скорость будет равна старой скорости плюс это изменение. Вы должны увидеть уравнение мысленным взором уже.
Это простейшее из трех уравнений для формального вывода. Начать с определение ускорения, расширьте член Δ v и решите для v как функцию t .
Поскольку ускорение также является первой производной скорости по со временем это уравнение можно вывести с помощью математического анализа. Просто переверните действие определения. Вместо того, чтобы дифференцировать скорость чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость. С ускорение предполагается постоянным, это довольно просто.
Символ v 0 (v ноль) называется начальной скоростью. Во многих текстах ему также дается символ и .Начальная скорость — это скорость, с которой движущийся объект имеет, когда это впервые становится важным в проблеме. Например, скажите метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальной скоростью будет скорость в то время, когда она была наблюдаемый. Но если бы проблема заключалась в определении его скорости при ударе, тогда его начальная скорость, скорее всего, будет той скоростью, которую он имел когда он вошел в атмосферу Земли. В этом случае ответ на: «Какая начальная скорость?» «Это зависит от обстоятельств».Это оказывается ответом на множество вопросов.
Символ v означает скорость через некоторое время Δ t после начальной скорости, часто называемой конечной скоростью. Конечная скорость зависит от решаемой задачи. Нет жесткого правила.
Последняя часть этого уравнения a Δ t — это изменение скорости от начального значения. Напомним, что a — это скорость изменения скорости, и что Δ t — это временной интервал с момента, когда объект имел начальную скорость v 0 .Скорость, умноженная на время, равняется изменению. Таким образом, если объект ускоряется при 10 мс -2 , через 5 с он будет двигаться на 50 мс -1 быстрее, чем это было изначально. Если бы он стартовал со скоростью 15 мс -1 , его скорость после 5 с ускорения была бы 65 мс -1 .
Время смещения
Смещение движущегося объекта прямо пропорционально скорости и время. Ускорение усугубляет эту простую ситуацию. Сейчас скорость также прямо пропорциональна времени.Попробуйте сказать это в слова и это звучит смешно. «Смещение прямо пропорционально времени и прямо пропорционально скорость, которая прямо пропорциональна времени «. Время в два раза больше, поэтому смещение пропорционально квадрату время. Автомобиль, разгоняющийся за две секунды, преодолеет в четыре раза больше расстояние автомобиля, ускоряющегося всего за одну секунду (2 2 = 4). Автомобиль, разгоняющийся за три секунды, преодолеет расстояние в девять раз (3 2 = 9).
Хотелось бы, чтобы все было так просто. Этот пример работает, только когда начальная скорость равно нулю. Изменение смещения пропорционально квадрату времени , когда ускорение постоянное, а начальная скорость равна нулю. Настоящий генерал оператор должен учитывать любую начальную скорость и как менялась скорость. Это приводит к ужасно беспорядочной пропорциональности. утверждение. Изменение смещения прямо пропорционально времени и пропорционально квадрату времени , когда ускорение постоянное.Функция, которая одновременно является линейной и квадратной. называется квадратичным, что позволяет нам значительно сжать предыдущее утверждение. Изменять в смещение является квадратичной функцией от времени при постоянном ускорении
Формулировки пропорциональности полезны, но не так кратки, как уравнения. Мы до сих пор не знаю, каковы константы пропорциональности для этого проблема. Единственный способ ответить на этот вопрос — через алгебру.
Начните с определения скорости, увеличьте Δ x и решите его для смещения.
[а]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, впервые опубликованному в Четырнадцатом Century в Мертон-колледже, Оксфорд (иногда называемый Мертонским колледжем). Правило). Когда ускорение постоянное, скорость будет равномерно изменяться от его начальное значение до его конечного значения, а среднее будет лежать на полпути между крайностями. Таким образом, средняя скорость — это просто арифметическая среднее значение начальной и конечной скоростей. Средняя скорость — это средняя конечной и начальной скоростей при постоянном ускорении.
Подставьте первое уравнение движения [1] в это уравнение (4) и упростите с намерением устранить v .
[б]
Наконец, подставьте [b] в [a] и решите x как функцию от t.
[2]
Поскольку скорость также является первой производной смещения по со временем это уравнение можно вывести с помощью математического анализа. По факту, это намного проще, чем использовать алгебру.Просто измените действие определение. Вместо того, чтобы дифференцировать смещение для определения скорости, проинтегрируйте скорость [1], чтобы найти смещение.
[а]
Символ x 0 (без нуля) — начальное смещение. Часто это значение равно нулю, и если это не так, мы можем сделать это так. если ты спросите меня: «Когда мы должны это сделать?» Я бы сказал: «Это зависит от проблемы», и предоставил бы вам решать. Нет правила, которое вы можете запомнить, это Это дело.Вы должны понять, что говорит уравнение, а затем научитесь применять его в конкретной ситуации. Точно так же x часто называют окончательным смещением, но это не делает его «последним смещением», скорее это смещение в конце временного интервала, в течение которого ускорение было постоянным.
Еще следует отметить сходство между уравнениями [2] и [a]. Когда ускорение равно нулю, наше второе уравнение движения меняется на противоположное. к преобразованному уравнению постоянной скорости.Как и предполагалось, смещение частично прямо пропорционально времени, а частично прямо пропорционально к квадрату времени.
[2]
[а]
Хотя символы скорости в двух уравнениях могут выглядеть по-разному, они действительно представляют одно и то же количество. Если нет ускорения, тогда скорость постоянна, что означает, что начальная скорость такая же, как и конечная скорость, такая же, как и средняя скорость. Член ускорения в конце — это поправка на постоянную уравнение скорости, чтобы учесть тот факт, что скорость равна меняется.Положительное ускорение увеличит смещение а отрицательное ускорение уменьшит его. Это именно то, что можно было ожидать. Если бы скорость объекта увеличивалась, он бы двигаться дальше, чем если бы он оставался с постоянной скоростью. Так же, если бы скорость объекта уменьшалась, у него было бы меньшее смещение чем если бы его скорость была постоянной. Приятно видеть, что уравнения вести себя реалистично. В противном случае вся эта математика была бы пустая трата времени.
Скорость-смещение
Мы только что видели, что скорость прямо пропорциональна времени и перемещению. пропорционально квадрату времени. Немного подумав, новое заявление о соразмерности должно быть очевидным. Изменение смещения пропорционально изменению в квадрате скорости при постоянном ускорении. Это утверждение особенно важно для безопасности вождения. Когда вы удваиваете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить.Увеличьте скорость втрое, и вам понадобится расстояние в девять раз больше. Как и предыдущие отношения, он также зависит от начальной скорости. К сожалению, определяя эффект использовать только рассуждения — настоящая рутинная работа. Вместо этого займитесь алгеброй.
Последние два уравнения описывают одну кинематическую переменную как функцию времени. Было бы неплохо, если бы у нас также было уравнение, которое было бы независимым времени. То есть мы хотим ответить на вопрос: «Какая связь между скоростью и смещением?» Метод этого должен быть очевиден.Мы должны объединить наши первые два уравнения движения вместе таким образом, чтобы исключить время как переменную. Самый простой способ сделать это — решить одно уравнение для времени, а затем подставьте его в другое. В второе уравнение движения является квадратичным и решает его относительно времени внесет в алгебру много гадостей. Должен быть очевидно, что решение первого уравнения движения [1] относительно времени и замена его на второй [2] будет более легким процессом.
Подставляем Δt = (v-v 0 ) / a
[3]
Как и ожидалось, смещение пропорционально квадрату скорости.(Начальная скорость в квадрате — это просто константа, с которой нужно иметь дело.) В отличие от первого и вторые уравнения движения, нет никакого преимущества в использовании исчисления вывести третье уравнение движения. Алгебра — это лучший способ.
Спираль постоянной линейной скорости (CLV) a) Скорость как функция сканирования …
Контекст 1
… Архимедова спираль с практически постоянной скоростью вдоль пути сканирования является результатом f (t *) = √ t * (фиг. 2а). Для этого случая дана скорость наконечника…
Context 2
… самый центр изображения v s CLV теоретически приближается к бесконечности. Однако в дискретных реализациях скорость уменьшается (фиг. 2a), поскольку высокие частоты для малого r в сигнале положения теряются из-за разнесения выборок. Когда t * 1 / (2πN) 2, скорость быстро приближается к постоянной. Аналогично, по направлению к самому центру изображения функция угловой частоты переходит в …
Context 3
… для дискретной реализации. Для поддержания постоянной линейной скорости требуется, чтобы угловая частота была более чем на два порядка выше в центре, чем на периферии изображения (фиг. 2b). Обратите внимание, что площадь под кривой скорости (фиг. 2a) представляет собой общую длину дуги (≈ 0,3 мм), а площадь под кривой угловой частоты (фиг. 2b) соответствует количеству петель N = 85. Эти значения остаются постоянными для всех описанных спиральных сканирований …
Контекст 4
… для дискретной реализации. Для поддержания постоянной линейной скорости требуется, чтобы угловая частота была более чем на два порядка выше в центре, чем на периферии изображения (фиг. 2b). Обратите внимание, что область под кривой скорости (фиг. 2a) представляет собой общую длину дуги (≈ 0,3 мм), тогда как область под кривой угловой частоты (фиг. 2b) соответствует количеству петель N = 85. Эти значения остаются постоянными для всех описанных спиральных сканирований …
Контекст 5
… для дискретной реализации. Для поддержания постоянной линейной скорости требуется, чтобы угловая частота была более чем на два порядка выше в центре, чем на периферии изображения (фиг. 2b). Обратите внимание, что площадь под кривой скорости (фиг. 2a) представляет собой общую длину дуги (≈ 0,3 мм), а площадь под кривой угловой частоты (фиг. 2b) соответствует количеству петель N = 85. Эти значения остаются постоянными для всех описанных спиральных сканирований …
Контекст 6
…. плотность для спирального сканирования CAV с параметрами сканирования, аналогичными тем, которые используются для фиг. 2 показан на фиг. 3c. Поскольку скорость сканирования в центре изображения близка к нулю, плотность данных чрезвычайно высока, достигая 74 выборок в центральных пикселях. И наоборот, плотность данных δ становится разреженной к периферии. Поскольку время сканирования T и количество циклов N такие же, как и у сканирования CLV (фиг. 2c), среднее значение η также равно единице, но значение падает до 0,5 на периферии, где элементы начинают недодискретизировать.Необходимость захвата информации на периферии изображения определяет частоту дискретизации и скорость спиралей CAV. Поэтому большую часть сканирования вблизи центра инструмент работает слишком медленно и тратит драгоценное время. Ни CLV, ни CAV спирали не идеальны для быстрой визуализации образца, но каждая из них обладает полезными свойствами. Оптимальная архимедова спираль сочетает в себе преимущества …
Контекст 7
… плотности для спирального сканирования CAV с параметрами сканирования, аналогичными тем, которые используются для фиг.2 показан на фиг. 3c. Поскольку скорость сканирования в центре изображения близка к нулю, плотность данных чрезвычайно высока, достигая 74 выборок в центральных пикселях. И наоборот, плотность данных δ становится разреженной к периферии. Поскольку время сканирования T и количество циклов N такие же, как и у сканирования CLV (фиг. 2c), среднее значение η также равно единице, но значение падает до 0,5 на периферии, где элементы начинают недодискретизировать. Необходимость захвата информации на периферии изображения определяет частоту дискретизации и скорость спиралей CAV.Поэтому большую часть сканирования вблизи центра инструмент работает слишком медленно и тратит драгоценное время. Ни CLV, ни CAV спирали не идеальны для быстрой визуализации образца, но каждая из них обладает полезными свойствами. Оптимальная архимедова спираль сочетает в себе преимущества …
Контекст 8
… идеальная архимедова спираль будет иметь самое короткое время сканирования при соблюдении механических ограничений инструмента. Функция времени f (t *) архимедовой спирали может иметь любую произвольную форму, приводящую к различным скоростям и частотам сканирования.Как видно на фиг. 2, механическое усиление резонанса может привести к большим отклонениям от предполагаемого пути сканирования и неточностям. Лучше всего, если частоты сканирования X, Y останутся значительно ниже резонанса. Точно так же высокие скорости наконечника приводят к скудным данным, фиг. 3, или высокие силы зонд-образец из-за плохой Z-пьезо-обратной связи, что делает скорость зонда не менее важной оптимизацией …
Контекст 9
… Спираль CLV удовлетворительно удовлетворяет всем критериям, за исключением первого критерия для идеальная форма волны сканирования.Что касается плотности данных, фиг. 2c, в пределах области сканирования спирали CLV имеют минимально возможную скорость, что идеально для получения стабильной обратной связи по топографии. Однако при высокой угловой частоте в центре возбуждение резонанса сканера в центре является существенным недостатком. На фиг. 2d, ошибка, вызванная механическим усилением сканера, очевидна. Резонанс находится на частоте 1600 Гц и имеет добротность 5. Прохождение через резонанс с частотами выше 8 кГц приводит к тому, что радиус становится ошибочно большим в центре.В результате в центре изображения нет данных. Наши алгоритмы создания изображений нацелены на восстановление недостающих данных. Тем не менее, сканер во время чириканья достаточно сильно развернулся, что датчики стали неточными, а пересекающиеся контуры имели противоречивые значения топографии для одного и того же места. Это привело к появлению звездообразных артефактов, которые очень хорошо видны в верхнем левом углу фиг. 5. Можно исправить спираль CLV, сделав сканирование в форме пончика [39], которое удаляет высокочастотную часть, но тогда данные отсутствуют в центре сканирования, где, вероятно, находятся интересующие детали.Мы обнаружили, что спираль CLV полезна только для самых медленных сканирований, хотя отметим, что CLV может иметь решающее значение для некоторых исследований, таких как мониторинг переключения сегнетоэлектрических доменов под смещенным наконечником, где скорость сканирования влияет на вероятность переключения и динамику. ..
Контекст 10
… Спираль CLV удовлетворительно удовлетворяет всем критериям, за исключением первого критерия идеальной формы сигнала сканирования. Что касается плотности данных, фиг. 2c, в пределах области сканирования спирали CLV имеют минимально возможную скорость, что идеально для получения стабильной обратной связи по топографии.Однако при высокой угловой частоте в центре возбуждение резонанса сканера в центре является существенным недостатком. На фиг. 2d, ошибка, вызванная механическим усилением сканера, очевидна. Резонанс находится на частоте 1600 Гц и имеет добротность 5. Прохождение через резонанс с частотами выше 8 кГц приводит к тому, что радиус становится ошибочно большим в центре. В результате в центре изображения нет данных. Наши алгоритмы создания изображений нацелены на восстановление недостающих данных.Тем не менее, сканер во время чириканья достаточно сильно развернулся, что датчики стали неточными, а пересекающиеся контуры имели противоречивые значения топографии для одного и того же места. Это привело к появлению звездообразных артефактов, которые очень хорошо видны в верхнем левом углу фиг. 5. Можно исправить спираль CLV, сделав сканирование в форме пончика [39], которое удаляет высокочастотную часть, но тогда данные отсутствуют в центре сканирования, где, вероятно, находятся интересующие детали.Мы обнаружили, что спираль CLV полезна только для самых медленных сканирований, хотя отметим, что CLV может иметь решающее значение для некоторых исследований, таких как мониторинг переключения сегнетоэлектрических доменов под смещенным наконечником, где скорость сканирования влияет на вероятность переключения и динамику. ..
CAV против CLV: краткие сведения об их различиях
Разъяснение различий между CAV и CLVCAV и CLV относятся к различным методам сканирования данных на вращающихся оптических носителях.Мы исследуем их определения, преимущества, недостатки и различия.
Определение постоянной угловой скорости (CAV):
Одна из двух схем управления скоростью вращения диска в дисководе. Постоянная угловая скорость поддерживает постоянную скорость вращения. Это означает, что линейная скорость диска под головкой больше при чтении или записи внешних дорожек. Это, в свою очередь, подразумевает либо изменение скорости передачи данных к головкам и от головок, либо количество битов на единицу длины по дорожке.(Хау «CAV» 2014)
Определение постоянной линейной скорости (CLV):
Способ управления вращением дисков в дисководе, при котором линейная скорость поверхности диска относительно головок чтения / записи поддерживается постоянной. Для достижения постоянной линейной скорости диск должен вращаться быстрее (с более высокой угловой скоростью) при чтении или записи дорожек ближе к центру. (Хоу «Постоянная линейная скорость», 2014 г.)
CAV против CLV: преимущества и недостатки
Преимущества CAV:
- Отдельные блоки данных можно адресовать по секторам и отслеживать напрямую
- Конструкция и изготовление CAV дисков проще и проще
- Для перемещения головки чтения / записи с ее текущего местоположения на конкретный адрес требуется всего лишь короткое движение
- Время ожидания вращения надлежащего сектора под головкой чтения-записи минимально
- Средний уровень шума ниже, чем у CLV
Недостатки CAV:
- Объем данных, которые могут храниться на внешних дорожках, ограничен емкостью хранения внутренних дорожек
Преимущества CLV:
- Гарантирует постоянную скорость доступа к данным (однако скорость вращения не постоянна )
Недостатки CLV:
- Произвольный доступ к данным медленный и сложный
- Заметные проблемы с производительностью современных компакт-дисков
- Средний уровень шума выше, чем у CAV
По сути, в чем разница между CAV и CLV?
Число битов на дорожку всегда остается постоянным с CAV.С другой стороны, поскольку CLV является линейным, скорость чтения выше при чтении данных у внешнего края диска и медленнее для данных ближе к центру диска.
Источники и полезные ресурсы:
- Столлингс, Уильям. Компьютерная организация и архитектура: проектирование для производительности. 10-е изд., Pearson Education, 2016.
- Мюллер, Скотт. Обновление и ремонт ПК, 15-я годовщина выпуска . 15-е изд., Que Publishing, 2003.
- Хау, Деннис.«Постоянная линейная скорость». Бесплатный онлайн-словарь по вычислительной технике, Департамент вычислительной техники Имперского колледжа, foldoc.org/constant+linear+velocity.
- Хау, Деннис. «Постоянная угловая скорость». Бесплатный онлайн-словарь по вычислительной технике, Департамент вычислительной техники Имперского колледжа, foldoc.org/cav
- Кенни, Дональд. «CAV VS CLV». Compuserve Benchmark And Standards Forum, 7 декабря 1997 г., donaldkenney.x10.mx/GLOSSARY/CAVVSCLV.HTM.
- «CAV.» Что такое CAV? Определение Webopedia, Webopedia, www.webopedia.com/TERM/C/CAV.html.
- «CLV.» Что такое CLV? Webopedia Definition, Webopedia, www.webopedia.com/TERM/C/CLV.html.
Разгон | Блог Гэри Гарбера
Ночь 5 Чтение: ускорение
Ускорение можно определить как изменение скорости за период времени. Обычно мы думаем об этом как об изменении скорости. Помните, что скорость — это вектор с величиной и направлением. Итак, есть два способа изменить скорость объекта.Мы можем изменить либо скорость, либо направление этой скорости (или и то, и другое одновременно!)
Как и скорость, ускорение — это вектор с величиной и направлением. Если направление скорости не меняется, то мы можем выразить ускорение как скорость изменения скорости,
Где a — ускорение, v — скорость, а t — время.
Поскольку скорость — это скорость изменения положения, мы могли бы также рассматривать ускорение как скорость изменения скорости изменения.Ускорение — это то, насколько мы ускоряемся (или замедляемся) за данную секунду.
Если вы смотрели рекламу автомобилей, они могли бы сказать вам, что автомобиль может разогнаться от 0 до 60 миль в час за 6 секунд. Таким образом, единицы для ускорения могут быть указаны как мили / час / секунда. Хотя это полезно для автомобилей и самолетов, в науке мы обычно выражаем скорость в метрах в секунду. Таким образом, единицами измерения ускорения будут метры в секунду в секунду. Фактически мы можем упростить это до квадратных метров / секунд.
Пример 1:
Предположим, самолет разгоняется от 0 м / с до 50 м / с за 20 секунд.Каким будет ускорение самолета?
Δv = 50,0 м / с
Δt = 20. с
а =?
В этом случае вы можете заметить, что время имеет только две значащие цифры из-за расположения десятичной точки (хотя скорость имеет три).
ПРИМЕР 2:
Если робот ускоряется из состояния покоя со скоростью 2, насколько быстро он движется через 4 секунды?
а = 2
t = 4 с
Δv =?
Используя, мы делаем алгебру, чтобы изолировать член скорости.
Обратите внимание, как в единицах измерения один коэффициент времени (секунды) отменяется, оставляя в качестве единиц измерения м / с.
Постоянное ускорение: Когда ускорение постоянное, мы можем легко использовать приведенное выше уравнение для определения изменения скорости. Если ускорение меняется, нам придется использовать несколько более сложные методы, чтобы найти изменение скорости. С аналитической точки зрения мы могли использовать исчисление. Или, используя компьютер или калькулятор, мы могли бы использовать любой из нескольких алгоритмов аппроксимации, чтобы найти изменение скорости, аналогично нахождению изменения положения.В случае непостоянного ускорения мы могли бы даже рассчитать скорость изменения ускорения, которая называется рывком и , когда вы резко дергаете или дергаете веревку.
Ускорение кругового движения. Уравнение ускорения для круговой траектории в простейшем случае нелинейного ускорения. Это называется центростремительным ускорением или центростремительным ускорением . Мы вернемся к этому случаю, когда будем изучать круговое движение.
Большинство реальных ускорений — это комбинация изменений скорости и изменения направления. Еще одно простое ускорение для анализа — это когда объект колеблется вперед и назад. Часто положение объекта будет соответствовать траектории синусоиды. В этом случае ускорение также является синусоидальной волной, и мы рассмотрим этот случай, когда перейдем к вибрационному движению.
Постоянное ускорение: графики
Когда ускорение постоянное и положительное, график a vs t будет выглядеть следующим образом.
Поскольку существует постоянное ускорение, скорость будет линейно увеличиваться во времени и будет выглядеть следующим образом. Конечно, если бы можно было вычислить наклон графика v vs t, можно было бы найти ускорение.
Как видим, скорость постоянно увеличивается. Это означает, что расстояние, пройденное за секунду, постоянно увеличивается. Точно так же наклон нашего графика зависимости положения от времени постоянно увеличивается и будет выглядеть, как на графике ниже.В этом случае форма кривой — парабола, а не линия. А функция, описывающая график, не линейная, а квадратичная. Любой квадратичный член будет содержать квадрат.
Резюме средней скорости в сравнении с мгновенной скоростью : Поскольку скорость меняется, мгновенная скорость не совпадает со средней скоростью. Мы нашли среднюю скорость, найдя наклон линии, образованной двумя точками. Поскольку скорость меняется, в этом случае мы фактически находим наклон хорды этого графика.По мере того, как хорды становятся меньше, мы приближаемся к пределу мгновенной скорости.
В пределе у нас больше нет хорды конечной длины. Вместо этого мы берем касательную к кривой и находим наклон этой касательной.
Мы сохраним представление уравнений положения при постоянном ускорении для следующего урока.
Какая формула для линейной скорости?
Чтобы определить линейную скорость, мы используем формулу v = rω v = rω = (3959mi) (π12radhr) = 3959π12mihr Линейная скорость приблизительно равна 1036.5 миль в час.
Также, как найти линейную скорость в физике?
Линейная скорость объекта может быть рассчитана по формуле : скорость равна расстоянию, деленному на время . В формуле v = линейная скорость, d = пройденное расстояние и t = время.
Здесь, какова формула линейной скорости и угловой скорости?
Связь между линейной скоростью и угловой скоростью можно записать двумя разными способами: v = rω или ω = v / r.
Также знать Почему V WR? V = wr для удобства клавиатуры использует w вместо omega, где w равно радианам в секунду, а r — радиус. Если период вращения равен t, то w = 2pi / t (два радиана пи в круге, деленные на один период вращения). Итак, v = 2pi * r / t.
Что означает линейная скорость?
Разница между линейной скоростью и угловой скоростью
| Линейная скорость | |
|---|---|
| Символ | Символ для линейной скорости — v . |
| Формула | v = ΔSΔt = 2πrt |
| Количество | Это векторная величина, которая подразумевает, что она имеет как величину, так и направление. |
| Измерительный блок | Мы измеряем линейную скорость в м / с. |
23 Связанные вопросы Найдены ответы
Что такое угловая скорость и линейная скорость?
Скорость определяется как скорость изменения положения за заданный период времени .… Линейная скорость — это не что иное, как скорость объекта, движущегося по прямой линии, тогда как угловая скорость — это то, насколько объект вращается, вращается или поворачивается, как хорошо резюмировал Чегг.
Что такое угловая скорость в терминах линейной скорости?Линейная скорость — это скорость по прямой (измеряется в м / с), а угловая скорость — это , изменение угла во времени (измеряется в рад / с, которое также может быть преобразовано в градусы).
В чем разница между линейной и угловой скоростью?Линейная скорость — это не что иное, как скорость объекта по прямой , тогда как угловая скорость — это то, насколько объект вращается, вращается или поворачивается, как хорошо резюмировал Чегг.… Итак, угловая скорость — это скорость изменения углового смещения объекта в единицу времени.
Какая связь между линейной и круговой скоростью?Зная о круговом движении, мы можем сказать, что величина линейной скорости частицы, движущейся по кругу, связана с угловой скоростью частицы ω соотношением υ / ω = r , где r означает радиус. В любой момент соотношение v / r = ω применимо к каждой частице, имеющей твердое тело.
Является ли V WR?где v — тангенциальная скорость, w — скорость вращения, а r i — радиус-вектор? Из прикрепленного изображения можно сделать вывод, что (каждая величина является вектором): w = r x v, также v = w x r и r = v x w.
Линейная скорость — это то же самое, что и скорость?Прямая ссылка на сообщение Алана «Линейная скорость — это скорость…» Линейная скорость — это скорость по прямой (измеряется в м / с), а угловая скорость — это изменение угла во времени (измеряется в рад / с, что также можно преобразовать в градусы).
Чему равна Омега?Угловая частота (ω), также известная как радиальная или круговая частота, измеряет угловое смещение в единицу времени. Его единицы измерения — градусы (или радианы) в секунду. Угловая частота (в радианах) больше обычной частоты (в Гц) в 2π: ω = 2πf . Следовательно, 1 Гц ≈ 6,28 рад / сек.
В чем разница между линейной скоростью и тангенциальной скоростью?Тангенциальная скорость — это линейная скорость любого объекта, движущегося по круговой траектории.Точка на внешнем крае поворотного стола перемещается на большее расстояние за один полный оборот, чем точка рядом с центром. … Другими словами, линейная скорость — это его тангенциальная скорость в любой момент времени.
Каково направление линейной скорости при круговом движении?В любой точке кругового движения направление линейной скорости частицы на касательное к круговой траектории .
Какова размерная формула угловой скорости?Есть два типа угловой скорости.
…
| Угловая скорость | |
|---|---|
| Поведение при преобразовании координат | псевдовектор |
| Вычисление других величин |
«Линейная скорость — это скалярная величина .”
Постоянна ли линейная скорость при равномерном круговом движении?При равномерном круговом движении линейная скорость имеет направление по касательной к окружности, образованной телом при равномерном круговом движении, которое постоянно меняется. Но величина линейной скорости постоянна .
В чем разница между линейной скоростью и скоростью вращения?Линейная скорость — это скорость и направление объекта, движущегося по прямой линии.… Скорость вращения — это скорость вращения объекта. Или, если быть более техническим, это скорость изменения углового положения . Измеряется в радианах в секунду.
В чем разница между линейной скоростью и линейным ускорением?Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления . Из «Равномерного кругового движения и гравитации» мы знаем, что центростремительное ускорение при круговом движении a c относится к изменениям направления скорости, но не ее величины.
Что такое формула линейного перемещения?Поскольку мы используем уравнение движения F = ma для описания линейного движения, мы можем использовать его аналог τ = dLdt = r × F τ = d L dt = r × F для описания углового движения.
В чем причина линейной скорости?Скорость — это скорость изменения положения объекта за определенный промежуток времени. Когда объект движется по прямому пути , связанная с ним скорость называется линейной скоростью.Он выражается как отношение пройденного расстояния ко времени.
Как рассчитать линейную скорость колеса?
Формула для линейной скорости
- s = frac {d} {t} Где,…
- линейная скорость = угловая скорость, умноженная на радиус вращения.
- т.е. v = омега, умноженная на r. v = линейная скорость (м / с)
- omega = угловая скорость (радиан / с) Где,…
- Решение: Сначала начните определять угловую скорость.…
- омега = 10,0 об / с.
- r = трещина {4} {2} = 2 м. …
- v = омега, умноженная на r,
При радиусе орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 км × 0,26 / ч ≈ 11 000 км / ч.