Угловая скорость вала: Расчет угловой скорости вала — Пример решения задачи
Анализ мгновенной угловой скорости коленчатого вала дизеля Текст научной статьи по специальности «Механика и машиностроение»
Анализ мгновенной угловой скорости коленчатого вала дизеля
М. Н. Панченко,
ст. преподаватель ФГБОУ ВО «Петербургский государственный университет путей сообщения Императора Александра I» (ПГУПС)
В. В. Грачев,
к. т. н., доцент, ПГУПС
А. В. Грищенко,
д. т. н.,
профессор, ПГУПС
С помощью аппарата вейвлет-преобразования можно существенно повысить достоверность контроля технического состояния многоцилиндрового дизеля по изменению мгновенной угловой скорости коленчатого вала и выявить неисправный цилиндр без привлечения дорогой аппаратуры.
Оценка качества рабочего процесса в цилиндрах многоцилиндрового транспортного дизеля по изменению мгновенной частоты вращения коленчатого вала (КВ) по-прежнему актуальна, так как дает возможность повысить параметрическую надежность не только двигателя, но и транспортного средства без использования дорогостоящих аппаратных средств контроля параметров рабочего процесса отдельных цилиндров [1]. Дополнительное преимущество сигнала мгновенной угловой
Рис. 1. Спектр частоты вращения коленчатого вала при исправном двигателе
Рис. 2. Спектр частоты вращения коленчатого вала при отключенном 5-м правом цилиндре двигателя
скорости — его относительно невысокая (по сравнению, например, с виброакустическими сигналами) зашумленность [2].
Периодический характер изменения угловой скорости определил в качестве основного инструмента для ее анализа преобразование Фурье, связывающее временной сигнал с его представлением в частотной области. Так, в [3] теоретически обосновывается и экспериментально подтверждается возможность оценки индикаторного момента и угла опережения зажигания отдельных цилиндров по параметрам амплитудного спектра кривой мгновенной скорости КВ бензинового двигателя 4Ч9,2/9,2.
Так, в [3] теоретически обосновывается и экспериментально подтверждается возможность оценки индикаторного момента и угла опережения зажигания отдельных цилиндров по параметрам амплитудного спектра кривой мгновенной скорости КВ бензинового двигателя 4Ч9,2/9,2.
В работе [4] предложен метод определения неисправности четырех- и шестицилиндровых бензиновых и дизельных двигателей по фазовой диаграмме спектра частоты вращения КВ, которая строится по фазовому спектру сигнала в полярных координатах. Анализ углового положения фазовых векторов отдельных гармоник спектра позволяет не только выявить отклонения в работе цилиндров, но и локализовать неисправный цилиндр.
Влияние неисправности ближайшего к датчику частоты вращения КВ цилиндра четырехтактного 12-цилиндрового V-образного дизельного двигателя на значения амплитуд спектра частоты вращения КВ исследовано в работе [5]. При этом влияние неисправности остальных цилиндров на амплитудный спектр не рассматривалось.
Расширение функциональных возможностей диагностической экспертной системы двигателя за счет использования спектра угловой скорости и ускорения КВ описано в [6, 7]. По параметрам спектра определяют степень неравномерности работы цилиндров, их герметичность и степень неуравновешенности двигателя. Однако конкретные взаимосвязи не приводятся.
В [2] установлена взаимосвязь между режимом работы (нагрузкой) и амплиту-
№ 4(77) 2018
«Транспорт Российской Федерации» | 59
Рис. 3. Выходное напряжение импульсного датчика частоты вращения коленчатого вала Рис. 4. Представление вейвлета Морле во временной области
 Вместе с тем результаты выполненных экспериментальных исследований свидетельствуют о невозможности достоверной локализации отказов топливной аппаратуры и газораспределительного механизма двигателя по параметрам спектра.
Вместе с тем результаты выполненных экспериментальных исследований свидетельствуют о невозможности достоверной локализации отказов топливной аппаратуры и газораспределительного механизма двигателя по параметрам спектра.Таким образом, даже для двигателей с малым числом цилиндров возникают сложности в определении взаимосвязи между параметрами спектра мгновенной угловой скорости КВ и техническим состоянием узлов двигателя. Локализация таким способом отказов многоцилиндровых двигателей представляет собой существенно более сложную задачу. Это связано с большим значением момента инерции вращающихся узлов и малым периодом действия отдельного цилиндра внутри одного рабочего цикла двигателя. Амплитудные спектры кривой напряжения датчика мгновенной угловой скорости КВ тепловозного дизельного двигателя 16ЧН26/26 для частоты вращения коленчатого вала п = 845 об/мин представлены для случаев исправного двигателя (рис. 1) и отключенного 5-го правого цилиндра (рис.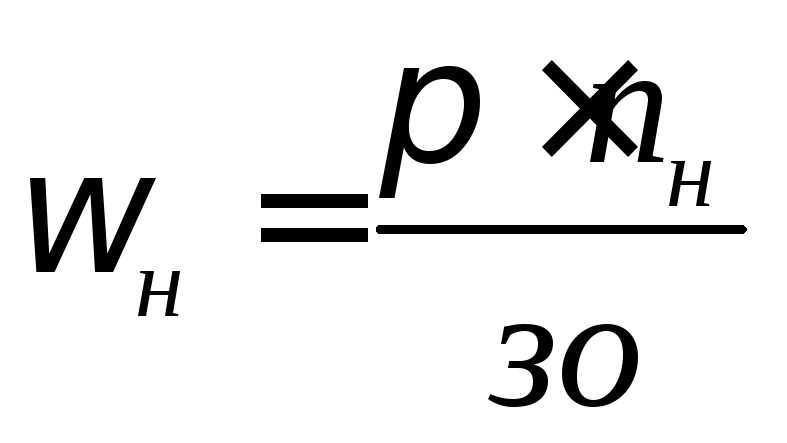
(1)
где 5 — параметр масштаба; т — сдвиг по времени, с;
ф* — комплексно-сопряженный материнский вейвлет.
В данном преобразовании материнский вейвлет (всплеск) — оконная функция, которая сдвигается по времени на величину т и меняет ширину (масштаб) вследствие изменения параметра 5. Разработаны материнские вейвлеты Хаара, Добеши, Симлета, Койфлета, Мей-ера, Морле, Шенона и т. д. [9].
В настоящей статье рассматривается возможность применения вейвлет-пре-образования для оценки технического состояния дизеля. В качестве диагностического сигнала используется выходное напряжение импульсного датчика частоты вращения КВ электронного регулятора ЭРЧМ30Т дизеля 5Д49 тепловоза 2ТЭ116У. Запись сигнала датчика осуществлялась с периодом дискретизации 5 мкс при работе дизеля под нагрузкой с частотой вращения КВ 845 об/мин в следующих режимах: включены все 16 цилиндров, отключен 5-й правый цилиндр, отключен 8-й правый цилиндр, отключены 5-й и 8-й правые цилиндры.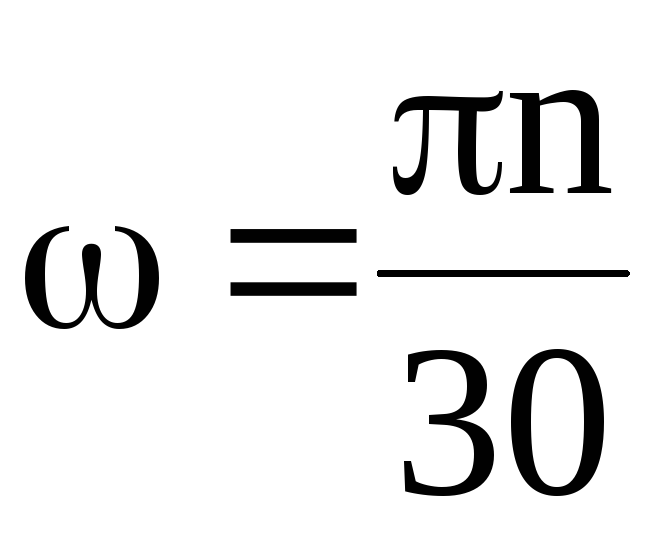
Результат вейвлет-анализа во многом определяется выбором материнского вейвлета, форма кривой которого должна в наибольшей степени совпадать с формой кривой диагностического сигнала исправного объекта. В данном случае сигнал частоты вращения периодический, по форме близкий к гармоническому (рис. 3). Поэтому для анализа сигнала в качестве материнского выбран вейвлет Морле (рис. 4), функция которого имеет вид
г
* = е С/гх*) х е1х2лх1:
Результаты вейвлет-преобразования (скалограммы) исходных сигналов с использованием вейвлета Морле (2) представлены на рис. 5, 6.
5, 6.
Скалограммы диагностических сигналов при всех работающих и одном отключенном цилиндре имеют заметные визуальные отличия значений амплитуды вейвлет-преобразования. Аналитическая оценка этих отличий может быть выполнена с использованием корреляционного анализа. Для этого выделяется фрагмент скалограммы каждого из сравниваемых сигналов, соответствующий двум полным оборотам КВ (рабочему циклу двигателя). Затем для скалограммы сигналов при всех работающих цилиндрах (исправный двигатель), определяется масштаб (сечение), которому соответствует максимальная
Количество отсчётов Рис. 5. Скалограмма частоты вращения при всех работающих цилиндрах
энергия преобразованного сигнала, т. е. выполняется условие
Я&Жт.Зтах)2 =
где т — количество отсчетов скалограммы, соответствующее 248 зубьям диска датчика; п — количество учитываемых масштабов скалограммы.
Зубья Интервалы
1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 0,977 0,999 0,984 0,999 0,993 0,998 0,974 0,999 0,987 0,999 0,977 0,990 0,975 0,997
2 0,989 0,999 0,993 0,998 0,996 0,998 0,986 0,999 0,987 0,999 0,989 0,989 0,986 0,999
3 0,990 0,999 0,994 0,999 0,996 0,999 0,973 0,996 0,988 0,995 0,979 0,995 0,986 0,998
4 0,990 0,999 0,995 0,997 0,994 0,999 0,973 0,998 0,977 0,999 0,990 0,994 0,973 0,996
5 0,991 0,998 0,989 0,997 0,996 0,999 0,974 0,999 0,989 0,994 0,982 0,985 0,971 0,999
6 0,981 0,999 0,996 0,996 0,991 0,999 0,986 0,998 0,978 0,999 0,992 0,992 0,969 0,999
7 0,981 0,996 0,980 0,998 0,998 0,994 0,974 0,999 0,978 0,994 0,984 0,997 0,967 0,999
8 0,992 0,999 0,981 0,998 0,994 0,999 0,986 0,997 0,979 0,999 0,986 0,999 0,966 0,999
9 0,982 0,999 0,991 0,998 0,995 0,998 0,986 0,999 0,990 0,984 0,994 0,990 0,964 0,999
10 0,983 0,998 0,967 0,997 0,988 0,998 0,974 0,997 0,980 0,999 0,988 0,999 0,963 0,999
11 0,993 0,995 0,996 0,979 0,996 0,999 0,994 0,999 0,997 0,998 0,995 0,978 0,977 0,994
12 0,984 0,998 0,967 0,994 0,990 0,998 0,975 0,997 0,983 0,999 0,982 0,997 0,961 0,995
13 0,993 0,994 0,991 0,985 0,997 0,999 0,987 0,997 0,993 0,997 0,992 0,999 0,987 0,993
14 0,954 0,998 0,968 0,996 0,979 0,991 0,975 1,000 0,984 0,999 0,986 0,999 0,975 0,996
15 0,993 0,998 0,991 0,979 0,990 0,999 0,986 0,997 0,985 0,999 0,995 0,999 0,974 0,993
Таблица 2. Матрица коэффициентов автокорреляции Пирсона при отключенном 5-м правом цилиндре
Матрица коэффициентов автокорреляции Пирсона при отключенном 5-м правом цилиндре
Зубья Интервалы
1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 0,989 0,982 0,933 0,973 0,948 0,993 0,974 0,999 0,941 0,997 0,949 1,000 0,983 0,997
2 0,977 0,988 0,947 0,983 0,963 0,997 0,975 1,000 0,957 0,999 0,965 1,000 0,983 0,996
3 0,988 0,974 0,920 0,996 0,976 0,990 0,987 0,998 0,954 0,996 0,979 1,000 0,969 0,987
4 0,975 0,991 0,955 0,988 0,959 0,995 0,976 0,999 0,968 0,999 0,978 0,999 0,982 0,994
5 0,973 0,965 0,929 0,986 0,956 0,976 0,976 0,991 0,925 0,995 0,976 0,996 0,968 0,993
6 0,970 0,986 0,943 0,983 0,970 0,994 0,977 0,999 0,961 0,998 0,975 0,999 0,992 0,991
7 0,967 0,982 0,937 0,980 0,968 0,993 0,977 0,988 0,958 0,984 0,974 0,996 0,968 0,997
8 0,963 0,979 0,930 0,994 0,980 0,992 0,996 0,998 0,954 0,998 0,973 0,999 0,992 0,989
9 0,959 0,986 0,944 0,985 0,964 0,997 0,977 0,998 0,968 0,997 0,971 0,999 0,982 0,999
10 0,912 0,955 0,915 0,983 0,961 0,980 0,977 0,991 0,927 0,979 0,953 0,995 0,969 0,999
11 0,950 0,980 0,932 0,980 0,958 0,997 0,976 0,990 0,964 0,977 0,969 0,999 0,983 0,994
12 0,962 0,994 0,964 0,996 0,984 0,996 0,996 0,998 0,962 0,999 0,982 0,999 0,993 0,994
13 0,938 0,984 0,942 0,995 0,952 0,996 0,976 0,986 0,960 0,999 0,967 0,999 0,985 0,998
14 0,908 0,981 0,913 0,974 0,949 0,996 0,976 0,984 0,958 0,985 0,967 0,994 0,975 0,998
15 0,946 0,978 0,930 0,998 0,964 0,996 0,976 0,991 0,956 0,998 0,967 0,999 0,995 0,999
хЮ»3
200 400 600 800 1000 1200 1400 1600
Количество отсчётов
Рис. 6. Скалограмма частоты вращения при отключенном 5-м правом цилиндре
6. Скалограмма частоты вращения при отключенном 5-м правом цилиндре
Таблица 1. Матрица коэффициентов автокорреляции Пирсона при всех работающих цилиндрах
№ 4 (77) 2018
«Транспорт Российской Федерации» | 61
Рис. 7. Сравнение матриц коэффициентов корреляции Пирсона для сигналов частоты вращения при всех работающих (синие маркеры) и одном отключенном (красные маркеры) цилиндрах
Далее выделенные фрагменты скало-грамм разбиваются на 16 (по количеству цилиндров) интервалов по 15 импульсов (зубьев) в каждом, сечения интервалов скалограмм сравниваются в пределах каждого сигнала с помощью коэффициента автокорреляции Пирсона
I lJ=1(xrX)x(Yj-Y)
TxY ~ I , г г’ (4)
Jl lj=1(Xj-x)\(Yj-?f
где Xj, Y—j-е значения скалограммы сигнала в сечении smax для каждого сравниваемого интервала; X, Y — средние значения скалограммы сигнала в сечении на каждом сравниваемом интервале.
Для двигателя со всеми исправно и равномерно работающими цилиндрами и идеальным профилем зубьев диска, на котором установлен датчик частоты вращения, все интервалы кривой напряжения датчика, отвечающие каждым 15 зубьям диска (работе одного цилиндра), и соответствующие им интервалы скалограммы сигнала напряжения будут одинаковыми, при этом коэффициенты взаимной автокорреляции интервалов скалограммы будут равны единице.
Изменение качества рабочего процесса в отдельных цилиндрах будет приводить к изменению мгновенной угловой скорости вращения коленчатого вала в определен-
ные периоды рабочего цикла двигателя. В результате будет меняться форма кривой напряжения датчика и ее скалограммы на соответствующих интервалах, что приведет к уменьшению коэффициентов взаимной автокорреляции (4) по интервалам.
Результаты определения коэффициентов автокорреляции скалограмм сигналов датчика частоты вращения КВ при всех работающих цилиндрах и при отключенном 5-м правом цилиндре приведены в таблицах 1, 2, а также на рис. 7.
7.
Значения коэффициентов автокорреляции интервалов скалограмм при всех работающих цилиндрах и отключенном 5-м цилиндре формируют отчетливые кластеры (рис. 7), что свидетельствует об изменении качества рабочего процесса в отдельных цилиндрах дизеля. При наличии датчика фазы, т. е. привязки сигнала датчика частоты вращения к верхней мертвой точке любого из цилиндров дизеля, взаимное расположение таких кластеров позволяет локализовать неисправный цилиндр.
Таким образом, применение аппарата вейвлет-преобразования позволяет существенно повысить достоверность контроля технического состояния многоцилиндрового дизеля по изменению мгновенной угловой скорости КВ. □
Литература
1. Грищенко А. В., Грачев В. В., Курилкин Д. Н. и др. Изменение системы технического обслуживания локомотивов // Наука и образование транспорту. — 2017. № 1. С. 25-27.
— 2017. № 1. С. 25-27.
2. Lin, T., Tan A. Lin Ma et al. Condition monitoring and fault diagnosis of diesel engine instantaneous angular speed analysis // Proceed. Institut. Mechan, Engineers/ Part C: J. Mechan. Engineer. Science. 2014. Vol. 229. Is. 2. P. 304-315.
3. Гребенников А. С., Гребенников С. А., Куверин И. Ю. и др. Развитие методологии диагностирования ДВС по показателям изменений угловой скорости коленчатого вала // Материалы международной научно-практической конференции «Информационные технологии и инновации на транспорте». 2015. С. 78-84.
4. Malaczynski G. W., Van der Poel R. Phase diagrams of different modes of misfire calculated from the digital Fourier transformation of angular crankshaft velocity // SAE Technic.l Paper 201001-0167. 2010. — URL: https://doi. org/10.4271/2010-01-0167.
5. Bulatovic Z. M., Stavljanin M. S., Tom-ic M. V. et al. Measurement and analysis of angular velocity variations of twelve-cylinder diesel engine crankshaft, // Mechanic. Systems and Signal Proces. 2011. Vol. 25. Is. 8. P. 3043-3061.
Bulatovic Z. M., Stavljanin M. S., Tom-ic M. V. et al. Measurement and analysis of angular velocity variations of twelve-cylinder diesel engine crankshaft, // Mechanic. Systems and Signal Proces. 2011. Vol. 25. Is. 8. P. 3043-3061.
6. Добролюбов И. П., Савченко О. Ф., Ольшевский С. Н. Принципы разработки компьютерной динамической модели автотракторных ДВС // Вестн. Новосибирск. гос. аграрного ун-та. 2014. № 2 (31). С. 141-146.
7. Способ определения технического состояния двигателей внутреннего сгорания и устройство для его осуществления: Пат. 2541072: МПК G01M 15/05 (2006.01) / Добролюбов И. П., Альт В. В., Савченко О. Ф., Ольшевский С. Н.; заявитель и патентообладатель Новосибирск. гос. аграрный ун-т. № 2012125779/06; заявл. 20.06.2012; опубл. 10.02.2015. Бюл. № 4.
8. Круглова Т. Н., Шурыгин Д.Н., Литвин Д. А. и др. Оценка эффективности различных методов анализа временных диагностических сигналов // Современные наукоемкие технологии. 2016, № 8-2. С. 237-241.
2016, № 8-2. С. 237-241.
9. Смоленцев Н. К. Основы теории вейв-летов. Вейвлеты в Matlab. М. : ДМК Пресс, 2014. — 628 с.
|
Bosch Rexroth KEB Control Techniques Parker Частотные преобразователи Широкий спектр качественных частотных преобразователей, услуги по подбору и модернизации станков и механизмов. Осуществляем официальные поставки по наилучшим ценам. Официальная поддержка клиентов и официальная гарантия. |
Motovario Wittenstein Alpha KEB Apex Мотор редукторы и редукторы Осуществляем поставки редукторов и мотор-редукторов разных типов от ведущих производителей. |
||
|
Абсолютные энкодеры Инкрементальные энкодеры Магнитные линейки Энкодеры, счетчики импульсов, токосъемники, индикаторы и пр. Поставляем официально все типы высокоэффективных энкодеров и индикаторов всех типов. Осуществляем оперативный подбор энкодеров под задачи заказчика. |
СТМЛ-1, ШМ-2, СТМ-2 СТМТ-2, MP-25, MTP-1 Системы линейного перемещения и модули линейного перемещения Разрабатываем и производим широкий спектр модулей и систем линейного перемещения. Производим системы линейных перемещений по индивидуальным заказам. |
||
Техника линейных перемещенийРельсовые направляющие SBC Цилиндрические направляющие Миниатюрные направляющие MID ШВП Техника и механические компоненты для систем линейных перемещений Разрабатываем и поставляем комплектующие для систем линейного перемещения. Производим системы линейных перемещений по индивидуальным проектам. |
Винтовые домкраты ZIMM Компоненты привода и трансмиссии ZIMM Домкраты и подъемно-транспортные механизмы Осуществляем поставки промышленных домкратов для производственных нужд, прецизионные домкраты. Предлагаем компоненты приводов и трансмиссии. |
||
Системы управленияКонтроллеры Fatek ЧПУ Delta Tau ЧПУ «СервоКон 2000» Системы управления, панели операторов Цифровые системы управления, современные системы ЧПУ, HMI и пр. Оказываемо полный комплекс услуг для систем ЧПУ. Осуществляем разработки и модернизации собственной высокоэффективной системы ЧПУ «Сервокон». |
Гибкие кабель-каналы CPS Гофрозащита CPS Flex Системы защиты кабелей, кабель-каналы Широкий спектр систем защиты кабелей, высоконадежные кабель-каналы для промышленного производства, гибкие кабель-каналы для жестких условий эксплуатации или специального назначения. |
НИОКР
Производим НИОКР, осуществляем услуги по разработке, проектированию, пуско-наладке широкого спектра механизмов, узлов, оборудования и станков. Осуществляем разработку, доработку, модернизацию и производство станков и механизмов, в том числе специального назначения (с уникальными характеристиками и/или функционалом) на базе собственного производства в России. Опыт работы более 15 лет.
НИОКР (что такое НИОКР?), определения, основные понятия, эффективность НИОКР.
НИОКР. Проекты НИОКР. Услуги НИОКР.
Заказать услуги НИОКР. Осуществление НИОКР.
НИОКР — Получить более подробную информацию о реализованных проектах.
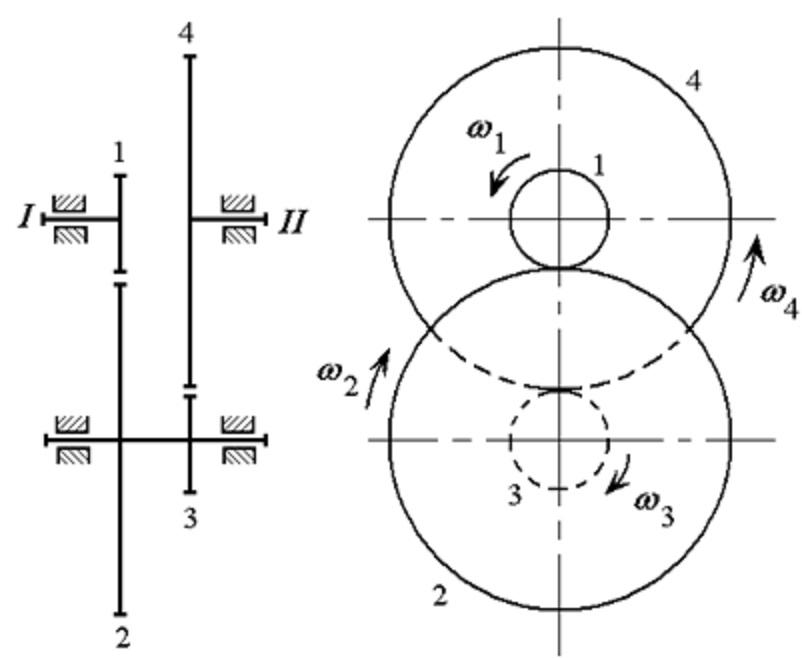
Угловая скорость вращения вала мешалки
В приведенных уравнениях ю = 2кп — угловая скорость вращения вала мешалки, и — тангенциальная составляющая скорости перемешиваемой жидкости на радиусе г. [c.313]
[c.313]Здесь Мщ, — крутящий момент на валу аппарата р — плотность перемешиваемой жидкости и — угловая скорость вращения вала Гм — радиус мешалки г — безразмерный текущий радиус мешалки Wt — безразмерная окружная скорость жидкости в аппарате. [c.83]
Пример [57]. Требуется определить зависимость частоты крутильных колебаний вала мешалки от вязкости жидкости, а также продолжительность времени, за которое амплитуда колебаний вала мешалки уменьшится в 10 раз после мгновенной остановки электродвигателя, если угловая скорость при равномерном вращении вала перед остановкой составляла Q. Массой вала по сравнению с массой лопастей можно пренебречь. Момент инерции массы лопастей J = 0,5 кг-м . Диаметр вала d = 0,005 м, длина вала 0,5 м. Коэффициент момента при наличии сил вязкого сопротивления движению лопастей а= 1,2 Н-м-с. Коэффициенты уравнения (160) п= 1,2/2 0,5= 1,21 = [c.107]
Материал из бункера 4 через патрубок поступает во вращающийся от вала 7 приводной конус 3 с приваренными, лопастями.
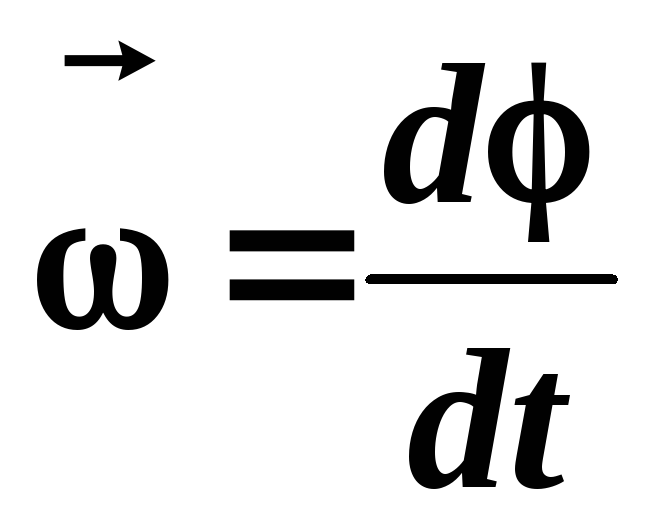 Сыпучая масса в конусе при значительной окружной скорости вращения (6—15 м/сек на верхнем краю) принимает форму параболоида вращения и, пересыпаясь через края конуса, попадает в пространство между корпусом I и конусом 5. К верхней опоре, размещенной на крышке корпуса, свободно подвешена лопастная мешалка, несущая две пары лопастей 2. Вращающийся в конусе материал передает часть своей кинетической энергии лопастям 2, которые начинают вращаться с уГловой скоро стью, значительно меньшей угловой скорости материала и тем более конуса. Дополнительное снижение угловой скорости лопастей 2 достигается тормозным устройством 5, размещенным на крышке, аппарата. Таким образом, в кольцевом пространстве создается разность окружных скоростей между лопастями и материалом, обеспечивающая лучшее перемешивание. Часть спускающегося вниз материала возвращается через окна внутрь конуса, где вновь поднимается вверх. Для устранения скопления материала на днище корпуса на приводной вал 7 посажен скребок. Выгрузка смеси производится из патрубка в днище аппарата.
Сыпучая масса в конусе при значительной окружной скорости вращения (6—15 м/сек на верхнем краю) принимает форму параболоида вращения и, пересыпаясь через края конуса, попадает в пространство между корпусом I и конусом 5. К верхней опоре, размещенной на крышке корпуса, свободно подвешена лопастная мешалка, несущая две пары лопастей 2. Вращающийся в конусе материал передает часть своей кинетической энергии лопастям 2, которые начинают вращаться с уГловой скоро стью, значительно меньшей угловой скорости материала и тем более конуса. Дополнительное снижение угловой скорости лопастей 2 достигается тормозным устройством 5, размещенным на крышке, аппарата. Таким образом, в кольцевом пространстве создается разность окружных скоростей между лопастями и материалом, обеспечивающая лучшее перемешивание. Часть спускающегося вниз материала возвращается через окна внутрь конуса, где вновь поднимается вверх. Для устранения скопления материала на днище корпуса на приводной вал 7 посажен скребок. Выгрузка смеси производится из патрубка в днище аппарата. Кратность циркуляции материала регулируется изменением числа оборотов приводного вала 7 и торможением подвесной мешалки (с лопастями 2). [c.141]
Кратность циркуляции материала регулируется изменением числа оборотов приводного вала 7 и торможением подвесной мешалки (с лопастями 2). [c.141]Исходные данные. Вал жесткий длина вала I = 5500 мм координаты центра тяжести мешалок = 2800 мм, = 4600 мм координаты опасных сечений по жесткости 2, = 600 мм (торцовое уплотнение вала) по прочности = 2750 мм (середина пролета вала) 2, = 2800 мм (шпоночная канавка) концентраторы напряжений в опасных по прочности сечениях — отсутствуют — шпоночная канавка угловая скорость вращения вала ш = 12,6 рад/с (и = = 120 об/мин) материал вала — легированная сталь 15ХМ (р = 7850 кг/м =2 10″ МПа) диаметр аппарата О = 2800 мм мешалки — пр опеллерные массы мешалок из, = 66 кг, = 66 кг диаметры мешалок (1 = 900 мм, с/ = 900 мм мощность, потребляемая одной мешалкой, N = Ы = Ы = 5000 Вт внутри аппарата имеются отражательнь(е перегородки и труба для передавливания реакционной массы рабочая температура в аппарате I = 80°С. [c.713]
С ростом угловой скорости вращения приводного вала увеличивается угол прецессии (рис.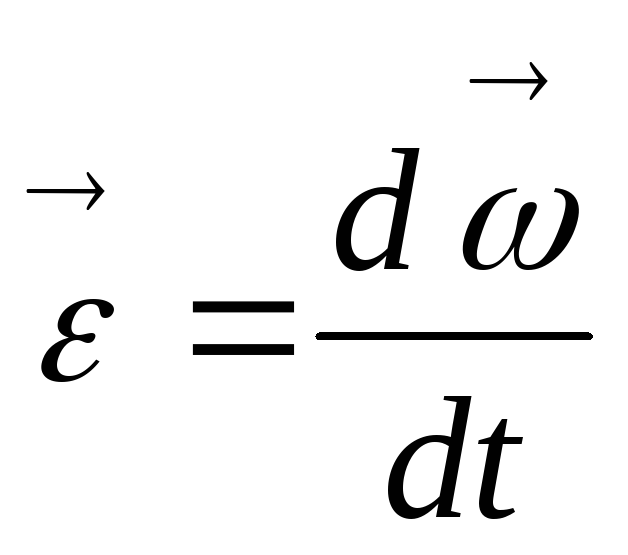 6.1.3.3), а коэффициент мощности растет от значения, соответствующего центральному расположению вала мешалки в гладкостенном аппарате, до значения (рис. 6.1.3.4), примерно равного коэффициенту мощности в аппарате с четырьмя отражательными перегородками [16]. [c.320]
6.1.3.3), а коэффициент мощности растет от значения, соответствующего центральному расположению вала мешалки в гладкостенном аппарате, до значения (рис. 6.1.3.4), примерно равного коэффициенту мощности в аппарате с четырьмя отражательными перегородками [16]. [c.320]
Масса, находящаяся в конусе, при значительной окружной скорости его принимает форму параболоида вращения и, пересыпаясь через края конуса, попадает в пространство между корпусом 4 и конусом 3. При этом масса пересекает зону, захватываемую лопастями 5, свободно подвешенными на крышке корпуса. Вращающийся в конусе материал передает часть своей кинетической энергии лопастям 5, которые при этом начинают вращаться с угловой скоростью, значительно меньшей, чем угловая скорость материала. Дополнительно угловая скорость лопастей снижается при помощи тормозного устройства 6, размещенного на крышке смесителя. Таким образом, в кольцевом пространстве вследствие разности окружных скоростей лопастей и материала обеспечивается интенсивное перемешивание материала.
 Часть опускающегося вниз материала возвращается через специальные окна в конус 3. Смесь выгружают через патрубок, расположенный в днище аппарата. Кратность циркуляции материала регулируется скоростью вращения приводного вала и торможением подвесной мешалки. [c.13]
Часть опускающегося вниз материала возвращается через специальные окна в конус 3. Смесь выгружают через патрубок, расположенный в днище аппарата. Кратность циркуляции материала регулируется скоростью вращения приводного вала и торможением подвесной мешалки. [c.13]При перемешивании больших объемов жидкости, когда требуется применение ддинньгх валов, целесообразно применение аппаратов с прецессирующей мешалкой (рис. 6.1.1.4). Вал мешалки 2 соединяется с валом привода с помощью шарнира Гука 5. В режиме перемешивания, помимо вращения вокруг собственной оси с угловой скоростью со, вал мешалки совершает также прецессионное движение относительно оси приводного вала, находясь в отклоненном от вертикальной оси на угол 5 положении. Таким образом, быстроходными мешалками относительно небольших диаметров удается активно перемешивать большие объемы жидкости. [c.307]
Ес.ии объем сосуда превышает 20 [131], то для обеспечения равномерности перемешивания применяют многоагрегатные (рис. IV.5, а) или прецессирующне (рис. IV.5, б) мешалки. Вал прецессирующей мешалки соединен с валом прдвода шарнирной муфтой, подобной шарниру Гука от карданного вала автомобиля. При вращении вокруг собственной оси с угловой скоростью (0 вал мешалки отклоняется от вертикали и движется по образующей конуса (процессирует) с некоторой угловой скоростью [c.183]
IV.5, а) или прецессирующне (рис. IV.5, б) мешалки. Вал прецессирующей мешалки соединен с валом прдвода шарнирной муфтой, подобной шарниру Гука от карданного вала автомобиля. При вращении вокруг собственной оси с угловой скоростью (0 вал мешалки отклоняется от вертикали и движется по образующей конуса (процессирует) с некоторой угловой скоростью [c.183]
Пропеллерные мешалки применяют для перемешивания жидкостей с вязкостью до 40 П. Основной элемент таких мешалок — пропеллер с = 0,25—0,35Да. Окружная скорость вращения достигает 10—20 м/с при угловой скорости до 1000 об/мин. Пропеллер устанавливают на высоте к — ём от дна аппарата. Общая рациональная высота жидкости составляет 4—5 м- При большей высоте на одном валу крепят два или более пропеллера. Пропеллерные мешалки рационально применять для растворения жидкостей, взвешивания твердых частиц при их массовом содержании в жидкости до 50%, взмучивания шламов с частицами размером до 100 мкм и содержанием твердой фазы до 10%, а также интенсификации теплообмена.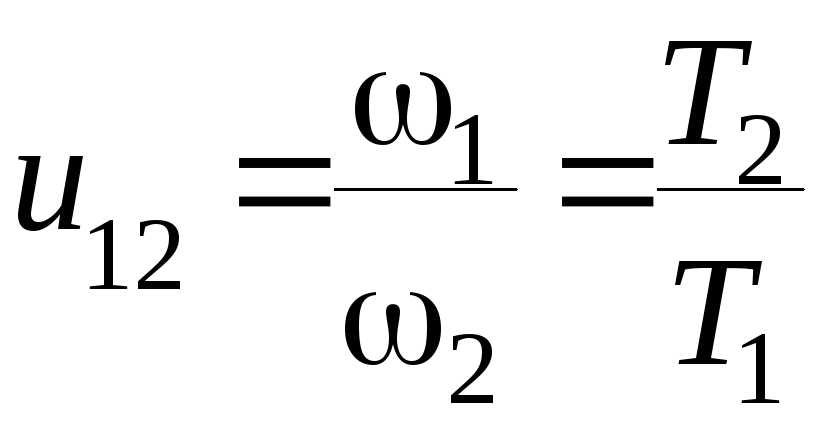 Во избежание образования застойных зон пропеллерные мешалки не следует устанавливать в аппаратах с плоским днищем. [c.195]
Во избежание образования застойных зон пропеллерные мешалки не следует устанавливать в аппаратах с плоским днищем. [c.195]
На рис. 199 представлены кривые изменения амплитуд колебаний в зависимости от частоты вращения вала с мешалкой в глицерине, воде и воздухе. Как следует из приведенных кривых движение вала в перемешиваемой жидкости протекает в режиме прямой синхронной прецессии до начала области неустойчивого вращения. С увеличением угловой скорости вала выше некоторого порогового значения со,, при о) > со,, амплитуды колебаний вала плавно или резко возрастают до недопустимых значений. Значение пороговой скорости со,,, при которой начинается возрастание амплитуд колебаний, может быть бoльпJe и меньше первой критической скорости вала. [c.285]
Скорость угловая критическая вала — Энциклопедия по машиностроению XXL
Скорость угловая критическая вала с дисками 212 [c.587]Так как в рассмотренном примере 6 частота вынужденных колебаний мотора равна угловой скорости вращения его вала, то критическая угловая скорость вала
[c.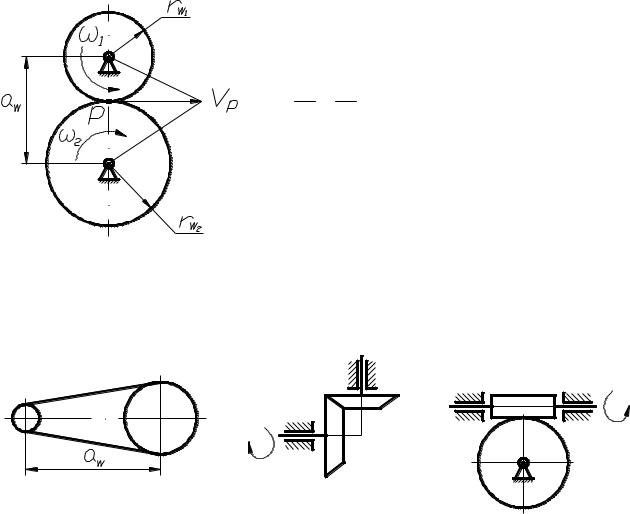 52]
52]
Отметим, что вал с несколькими дисками имеет несколько критических угловых скоростей и критическое состояние наступает при совпадении угловой скорости с любой из критических скоростей. [c.245]
Вал, работающий при угловой скорости, меньшей критической, принято называть жестким, а при угловой, скорости, большей критической, — гибким. Если на валу укреплено несколько дисков, то колебательная система вал — диски имеет несколько степеней свободы, и тогда должно быть несколько критических (ре- [c.131]
Внутри областей устойчивости выясняется характер зависимости прогибов вращающегося вала от скорости его вращения (при некоторой фиксированной величине неуравновешенности). Те угловые скорости, при которых прогибы вала достигают максимальных значений, могут оказаться в эксплуатации опасными такие скорости называют критическими. [c.46]
При угловой скорости вала, равной величине угловой частоты собственных колебаний вала при данной скорости вращения, возникает критическое состояние вала вследствие неуравновешенности. Угловая скорость, равная частоте собственных колебаний прямой прецессии (при этой же скорости вращения), называется критической скоростью прямой прецессии вала или просто критической скоростью вала.
[c.116]
Угловая скорость, равная частоте собственных колебаний прямой прецессии (при этой же скорости вращения), называется критической скоростью прямой прецессии вала или просто критической скоростью вала.
[c.116]
Как правило, неуравновешенность вала вызывает такое колебательное движение, которое приводит к прямой прецессии. При со = со о, т. е. при угловой скорости, равной критической, скорость прецессии равна угловой скорости вала. Такая прецессия называется прямой синхронной прецессией. Однако в некоторых случаях, как будет показано в дальнейшем, неуравновешенность может вызвать обратную прецессию. Поэтому наряду с критической скоростью прямой прецессии иногда рассматривают критическую скорость соо обратной прецессии, которая удовлетворяет соотношению СОо = —А, (соо). [c.117]
Задача о колебаниях вала с диском, расположенным симметрично по отношению к опорам, была первой задачей в области изгибных колебаний вращающихся валов, разрешавшейся теоретически и экспериментально. В 1869 г. Рэнкиным [10] впервые был сделан теоретический анализ колебательного движения гибкого вала с диском, а в 1889 г. Лавалем была построена турбина с гибким валом, рабочая угловая скорость которого была выше его критической скорости. Применение такого вала было основано на использовании обнаруженного эффекта самоцентрирования вала, проявляющегося в закритической области вращения. Если при скорости вращения ниже критической всякая неуравновешенность детали (диска), прикрепленной к валу, вызывает большие колебания и динамические реакции подшипников, то при скорости вращения выше критической, как показали теория и опыт, колебания успокаиваются и практически почти уничтожаются при дальнейшем возрастании скорости. В этом, собственно, и состоит явление самоцентрирования, удачно использованное для создания новой для того времени конструкции вала турбины.
[c.118]
В 1869 г. Рэнкиным [10] впервые был сделан теоретический анализ колебательного движения гибкого вала с диском, а в 1889 г. Лавалем была построена турбина с гибким валом, рабочая угловая скорость которого была выше его критической скорости. Применение такого вала было основано на использовании обнаруженного эффекта самоцентрирования вала, проявляющегося в закритической области вращения. Если при скорости вращения ниже критической всякая неуравновешенность детали (диска), прикрепленной к валу, вызывает большие колебания и динамические реакции подшипников, то при скорости вращения выше критической, как показали теория и опыт, колебания успокаиваются и практически почти уничтожаются при дальнейшем возрастании скорости. В этом, собственно, и состоит явление самоцентрирования, удачно использованное для создания новой для того времени конструкции вала турбины.
[c.118]
Т. е. вал должен вращаться с угловой скоростью ниже критической.
 В противном случае его движение будет неустойчивым.
[c.126]
В противном случае его движение будет неустойчивым.
[c.126]В тех случаях, когда двигатель, приводящий вал во вращение, обладает достаточно большой мощностью, имеется возможность осуществить нарастание угловой скорости вала по тому или иному заданному закону, как это было предположено выше. Но если мощность двигателя мала, то при переходе через критическую скорость угловая скорость вала в зоне, близкой к критической, будет изменяться в зависимости от общих динамических свойств системы вал — двигатель ) и, во всяком случае, ее нарастание будет сильно ограничено. Возможно также и застревание вала на критической скорости и тогда любое увеличение энергии, подаваемой на вращение вала, совершенно не приводит к увеличению угловой скорости, а способствует только увеличению амплитуд колебаний, [c.169]
Типичная характеристика имеет вид нисходящей кривой, т. е. момент уменьшается с увеличением скорости. Если (фиг. 74) построить кривую зависимости момента сопротивления со стороны вала, слагающегося из сопротивления колебательному движению и сопротивления рассеяния энергии (кривая 1), и нанести характеристику двигателя (кривая 2), то точка пересечения А кривых определит угловую скорость стационарного режима вала.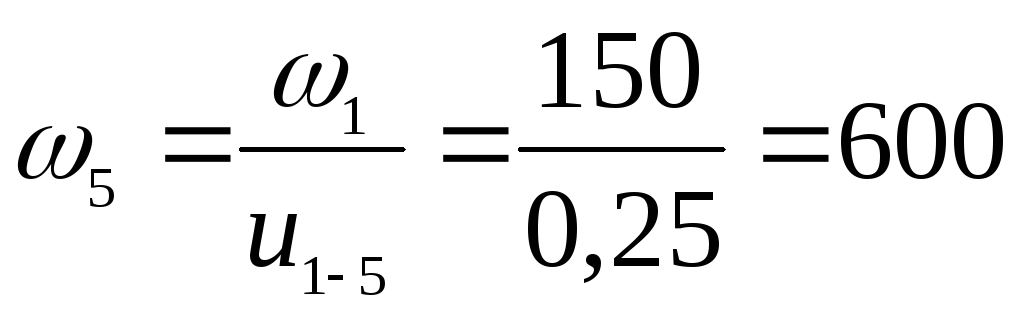 Для кривой 2 эта скорость расположена до критической если же требуется вращение со скоростью выше критической, то характеристика (кривая 3), обеспечивающая медленный про-
[c.410]
Для кривой 2 эта скорость расположена до критической если же требуется вращение со скоростью выше критической, то характеристика (кривая 3), обеспечивающая медленный про-
[c.410]
При угловых колебаниях вала с диском возникает гироскопическое действие диска, повышающее значенпе частоты и критической скорости в области прямой прецессии (Q и (о одного знака) и снижающее эти значения в области обратной прецессии (Q и со разных знаков). [c.410]
На рис. 13, б, в изображено взаимное расположение точек О, В и С при угловых скоростях меньше (рис. 13, б) и больше (рис. 13, в) критической. Теоретические и экспериментальные исследования показывают, что при угловых скоростях меньше и больше критической вал динамически устойчив, т. е. если по каким-либо причинам прогиб вала увеличивается, то после устранения этих причин он возвращается в первоначальное положение. На критической же угловой скорости вал динамически неустойчив. [c.54]
Пусть имеется вполне уравновешенный ротор, вал которого вращается с первой критической скоростью в слегка изогнутом состоянии.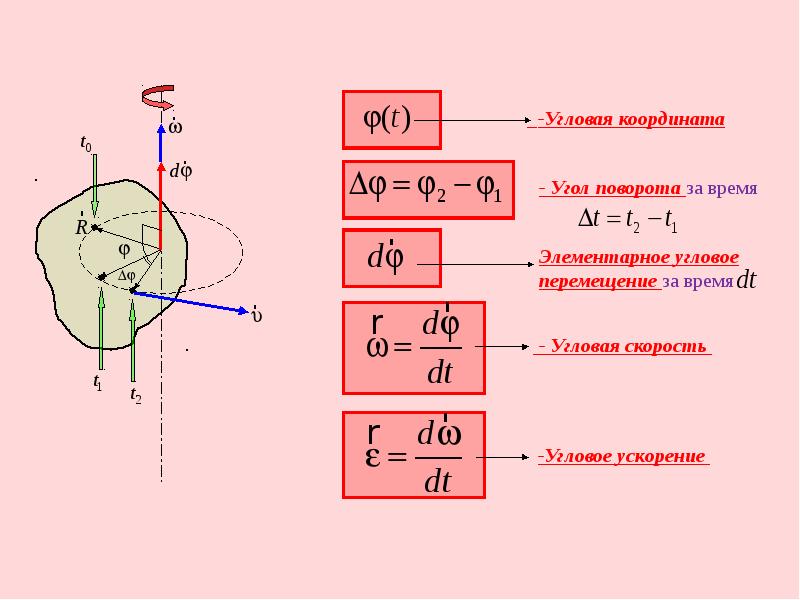 Положим, что угловая скорость происходящего вследствие этого возмущенного движения центра вала такая же, как и угловая скорость вращения самого вала. Это значит, что некото-
[c.65]
Положим, что угловая скорость происходящего вследствие этого возмущенного движения центра вала такая же, как и угловая скорость вращения самого вала. Это значит, что некото-
[c.65]
Этот метод применяется для определения первой критической угловой скорости многодисковых роторов, валы которых имеют переменные сечения. [c.279]
При колебаниях с первой критической угловой скоростью все массы вала одновременно достигают максимального удаления от положения равновесия или одновременно через него проходят. [c.279]
Низкие нормы допускаемых напряжений в турбинных валах приходится принимать и по другим соображениям. Обыкновенно размеры вала подбирают таким образом, чтобы нормальная угловая скорость, при которой вал работает, была значительно ниже так называемой критической скорости. Для повышения критической скорости приходится вал делать по возможности более жестким ). [c.255]
Для устойчивой работы вала межд) его рабочей угловой скоростью Q критической скоростью должны бьт выдержаны определенные соотношения а именно
[c. 366]
366]
Из уравнения (3) следует, что при совпадении угловой скорости с критической угловой скоростью прогибы вала неограниченно возрастают. [c.432]
Из анализа формулы (а) следует, что с ростом угловой скорости со увеличивается и прогиб у, а при (с, = у р /т прогиб у->со. Таким образом, при угловой скорости, называемой критической, должно произойти разрушение оси или вала. Следовательно, критическая угловая скорость оси или вала [c.283]
Таким образом, для отсутствия резонанса угловая скорость оси или вала при установившемся движении должна быть меньше или больше критической скорости. О приближении угловой скорости оси или вала к критической свидетельствует появление сильной вибрации. При продолжительной работе в области резонанса разрущение оси или вала неизбежно. Однако вследствие различных сопротивлений, возникающих при колебаниях, разрушение осей и валов не может произойти мгновенно и при быстром переходе в закритическую область работоспособность осей и валов полностью сохраняется. [c.284]
[c.284]
Решение. Угловая критическая скорость вращения вала находится по формуле (695) [c.483]
Из уравнения (223) следует, что потеря динамической устойчивости вала (или, иначе, явление резонанса) наступает при некоторых определенных значениях угловой скорости которые называют критическими скоростями для данного вала. [c.552]
Чтобы избежать явлений резонанса, угловая скорость м вращения вала должна быть ниже или выше критической Теоретически безразлично, будет ли ш > 1 или числа оборотов шпинделя обусловлены [c.379]
Таким образом, при критической угловой скорости сбалансированный вращающийся вал находится в равновесии при любой величине прогиба (конечно, лишь постольку, поскольку справедлива линейная теория). [c.414]
При угловой скорости, меньшей критической (рис. 7.5, а), радиус окружности, по которой движется центр масс диска, складывается из трех величин радиального зазора б, прогиба вала у и эксцентриситета а. Уравнение равновесия записывается в виде
[c.340]
7.5, а), радиус окружности, по которой движется центр масс диска, складывается из трех величин радиального зазора б, прогиба вала у и эксцентриситета а. Уравнение равновесия записывается в виде
[c.340]
Валы центрифуг по характеру работы разделяют на гибкие и жесткие. Гибкими называют валы, работающие при угловых скоростях, превышающих критическую (со > ю,,р), жесткими — валы, рабочая угловая скорость которых меньше критической (со[c.267]
Из этого уравнения видно, что прогиб вала w быстро увеличивается с приближением значения угловой скорости вращения вала собственной частоте поперечных колебаний вала. Критическая [c.549]
Быстровращающиеся детали машин не могут быть идеально сбалансированы и в практических случаях всегда возникают инерционные силы дисбаланса, уводящие вращающуюся деталь (вал, ротор) от оси Вращения. При этом, как показывает опыт, при определенных угловых скоростях вращения, называемых критическими, имеют место наибольшие прогибы системы и наиболее сильная ее раскачка. При дальнейшем увеличении числа оборотов раскачка уменьшается. Этому явлению можно дать довольно простое объяснение, рассматривая упругую систему как колебательную, а силы дисбаланса — как возмущающие силы.
[c.495]
При дальнейшем увеличении числа оборотов раскачка уменьшается. Этому явлению можно дать довольно простое объяснение, рассматривая упругую систему как колебательную, а силы дисбаланса — как возмущающие силы.
[c.495]
Вал, работающий при угловой скорости, меньшей критической, принято называть жестким, а при угловой скорости, большей критической — гибким. Если на валу укреплено несколько дисков, то колебательная система вал — диск имеет несколько степеней свободы, и тогда должно быть несколько критических (резонансных) угловых скоростей. Наименьшая из этих скоростей называется первой резонансной. С учетом того, что при балансировке роторов принимается во внимание упругость ппор ротора, ГОСТ 19534-70 дает следующее определение жестких и гибких роторов К жестким роторам относятся роторы, у которых после балансировки в двух произвольно выбранных плоскостях коррекции на частоте вращения при балансировке ниже первой резонансной системы ротор — опоры значения остаточных дисбалансов в плоскостях опор не превзойдут допустимых значений на эксплуатационных частотах вращения. Все остальные роторы относятся к гибким .
[c.328]
Все остальные роторы относятся к гибким .
[c.328]
Основное практическое значение имеет положительная синхронна. прецессия Л = 1, т. е. когда угловая скорость плоскости изогнутого вала равна по величине и совпадает по направлению с угловой скоростью вала. Гироскопический момент в этом случае уменьшает изгиб вала, т. е. повышает критическую скорость. При наличии возбуждаюншх сил соответствующей частоты возможна [c.374]
Основное практическое значение имеет положительная синхронная прецессия А = 1, т. е. когда угловая скорость плоскости изогнутого вала равна по величине и совпадает по направлению с угловой скоростью вала. Гироскопический момент в этом случае уменьшает изгиб вала, т. е. повышает критическую скорость. При наличии возбуждающих сил соответствующей частоты наблюдается также отрицательная синхронная прецессия, т. е. вращение плоскости изогнутого вала с угловой скоростью, равной по величине и противоположной по направлению угловой скорости вала. При этом гирескопический момент ка-кой-либо массы будет равен
[c.275]
При этом гирескопический момент ка-кой-либо массы будет равен
[c.275]
При вращении вала, несущего несбалансированный диск, ось вала под действием центробежной силы прогибается и совершает прецес сионное движение, описывая некоторую поверхность вращения. С увеличением угловой скорости прогибы оси возрастают и становятся особенно значительными с приближением угловой скорости к некоторому определенному (критическому) значению соответствующее число оборотов также называют критическим. При дальнейшем увеличении угловой скорости сверх критического значения прогибы оси вала вновь [c.324]
При совпадении или кратности частоты возмущающих сил и частоты собственных колебаний оси или вала наступает резонанс, при котором адшлитуда колебаний оси или вала резко возрастает и может достигнуть такого значения, при котором ось или вал разрушится. Соответствующую резонансу угловую скорость оси или вала называют критической. [c.373]
Расчет критической угловой скорости вала центрифуги. Устойчивая работа вала нарушается при приближении его скорости к критической. При этом увеличивается прогиб вала. На рис. 232 приведена схема вала для наиболее типичного случая консольного закреилепия ротора центрифуги. Вал центрифуги совершает двойное вращательное движение. Кроме вращательного движения около собственной изогнутой оси, вал совершает вращательное
[c.274]
Устойчивая работа вала нарушается при приближении его скорости к критической. При этом увеличивается прогиб вала. На рис. 232 приведена схема вала для наиболее типичного случая консольного закреилепия ротора центрифуги. Вал центрифуги совершает двойное вращательное движение. Кроме вращательного движения около собственной изогнутой оси, вал совершает вращательное
[c.274]
Электрический мотор массы N[ установлен на балке, жесткость которой равна с. На вал мотора насажен груз массы тИг на расстоянии / от оси вала. Угловая скорость мотора (О = onst. Определить амплитуду вынужденных колебаний мотора н критическое число его оборотов в минуту, пренебрегая массой балки и сопротивлением движению. [c.272]
Оиределить критическую угловую скорость (относительно поперечных колебаний) легкого вала, несущего иосредипс диск веса Р. Рассмотреть следующие случаи 1) вал на обоих концах опирается на длинные иодшииники (концы можно считать заделанными) 2) на одном конце вал опирается на длинный подшипник (конец заделан), а на другом — на короткий подшипник (конец оперт). Жесткость вала на изгиб Е], длина вала /.
[c.416]
Жесткость вала на изгиб Е], длина вала /.
[c.416]
Анализ комплексной системы автоматического регулирования частоты вращения вала дизельного двигателя и температуры охлаждающей жидкости — page 16
В.А. Марков, С.Н. Девянин, Л.Л. Михальский
16
Сначала рассчитывался канал регулирования частоты вращения
коленчатого вала, затем контур регулирования температуры охлаж-
дающей жидкости. Результаты расчетов канала регулирования часто-
ты вращения коленчатого вала ( рис. 7) свидетельствуют о том, что
исходная САР с чисто пропорциональным регулятором обеспечивает
степень неравномерности (наклон) регуляторной характеристики
δ, % (рис.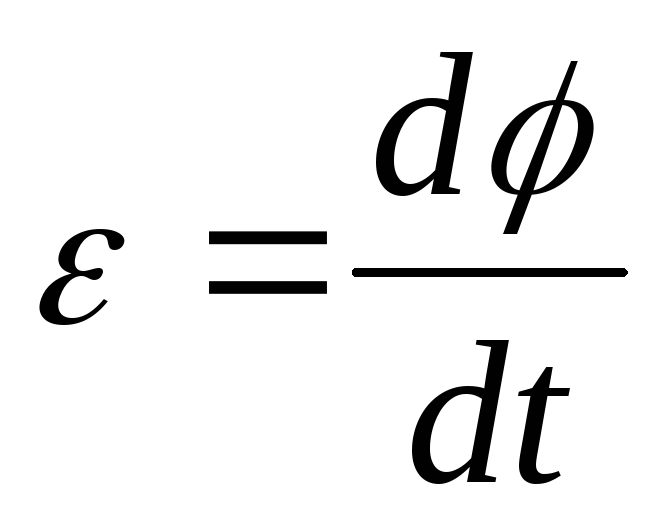 7,
7,
а
и 8):
д.х.х max д.ном
д.ном
100,
ω − ω
δ =
⋅
ω
где ω
д.ном
— номинальная угловая скорость вала двигателя; ω
д.х.х max
—
угловая скорость вала двигателя на режиме холостого хода.
Рис. 8.
Зависимость степени неравномерности регуляторной характеристи-
ки САР частоты вращения вала дизеля (
а
) и провала угловой скорости (ча-
стоты вращения) в переходном процессе наброса полной нагрузки (
б
) от
коэффициента усиления регулятора по нагрузке
k
н
дизеля типа Д-240 с ко-
эффициентом усиления П-регулятора
k
п
= 10
Эта САР реализует δ = 7 % при провале частоты вращения в пе-
реходном процессе наброса полной нагрузки –7,2 % (рис. 7,
7,
а
и 9).
Наилучшее качество процесса регулирования достигается при коэф-
фициенте усиления регулятора по нагрузке
k
н
= 0,79 (рис. 7,
д
).
В этом случае обеспечивается нулевая степень неравномерности ре-
гуляторной характеристики (δ = 0), т. е. реализуется астатическая
САР. Провал частоты вращения в переходном процессе наброса пол-
ной нагрузки дизеля составил Δω
д
= 2,2 %, а продолжительность пе-
реходного процесса
t
п
≈
0,3 с. Эти показатели качества процесса ре-
Эти показатели качества процесса ре-
гулирования значительно лучше аналогичных показателей, допусти-
мых для САР первого класса точности (Δω
д
= 5 %,
t
п
= 2 с).
На втором этапе исследований рассчитывался контур регулирова-
ния температуры охлаждающей жидкости (см. рис. 9). Следует отме-
тить, что подсистема регулирования температуры охлаждающей жид-
кости значительно более инерционная, чем подсистема регулирования
частоты вращения, поэтому переходные процессы в этой подсистеме
Вопросы»Угловая скорость вращения вала автомобильного двигателя и угловая скорость вращения колес автомобиля измеряются в оборотах в минуту|Поступи в ВУЗ
Угловая скорость вращения вала автомобильного двигателя и угловая скорость вращения колес автомобиля измеряются в оборотах в минуту
создана: 20. 03.2020 в 10:01
03.2020 в 10:01
…………………………………………
liliana :
Угловая скорость вращения вала автомобильного двигателя ωдвиг
и угловая скорость вращения колёс автомобиля ωкол
измеряются в оборотах в минуту. Эти величины связаны соотношением
ωкол = ωдвиг / (kb)
где k — передаточное число дифференциала автомобиля, а b — передаточное число
коробки передач при выбранной передаче.
В таблице указаны передаточные числа для автомобиля «Лада-Калина».
|
|
Коробка передач |
|
|||||
|
|
1-я |
2-я |
3-я |
4-я |
5-я |
Задняя |
Дифференциал |
|
|
пер. |
пер. |
пер. |
пер. |
пер. |
|
|
|
Передаточное число |
3,636 |
1,950 |
1,357 |
0,941 |
0,784 |
3,500 |
3,706 |
Водитель разгонялся на 5-й передаче, пока число оборотов двигателя не достигло 2000 об/мин.
В этот момент водитель, не меняя скорости, включил 2-ю передачу.
Найдите угловую скорость вращения вала двигателя после переключения.
Результат округлите до целого числа оборотов.
Ответ: 4974
Физики разогнали «спиннеры» до миллиарда оборотов в секунду
Jonghoon Ahn et al. / Phys. Rev. Lett.
Две команды физиков независимо разогнали с помощью лазеров нанометровые «спиннеры» до скорости порядка одного миллиарда оборотов в секунду — самой высокой скорости вращения, полученной в лаборатории. Первая группа из Швейцарской высшей технической школы Цюриха (ETH Zurich) заставляла вращаться наночастицу кремнезема, а вторая группа, состоящая из китайских и американских исследователей, использовала в качестве «спиннера» наногантелю.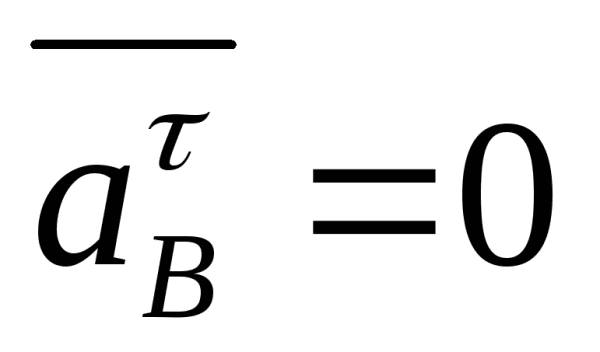 Работа ученых поможет лучше понять такие тонкие эффекты, как вращение Казимира, связанное с квантовыми флуктуациями вакуума. Статьи опубликованы в Physical Review Letters [1, 2], кратко о них сообщает Physics, препринты работ выложены на сайте arXiv.org [1, 2].
Работа ученых поможет лучше понять такие тонкие эффекты, как вращение Казимира, связанное с квантовыми флуктуациями вакуума. Статьи опубликованы в Physical Review Letters [1, 2], кратко о них сообщает Physics, препринты работ выложены на сайте arXiv.org [1, 2].
Скорость вращения любого объекта ограничена пределом его прочности. Чем быстрее вращается объект, тем большую скорость развивают его частицы и тем большая сила нужна, чтобы заставлять их повернуть и удерживать тело в целости. Другими словами, при увеличении скорости растет центробежная сила, которая стремится «разорвать» тело. Впрочем, называть центробежную силу «силой» не совсем правильно, поскольку она возникает только в неинерциальной системе отсчета (подробнее о ее природе можно прочитать в этой заметке).
Заметнее всего действие этой «фиктивной силы» проявляется в точках, наиболее удаленных от центра вращения объекта: F = mω2r, где m — масса точки, r — ее расстояние до центра, а ω — угловая скорость. Из-за этого частота вращения макроскопических объектов редко превышает тысячу оборотов в секунду. Например, частота вала газогенератора двигателя PW207K вертолета «Ансат» может достигать 60000 оборотов в минуту (1000 оборотов в секунду), а турбина двигателя CFM56, который устанавливается на самолетах фирм Boeing и Airbus, вращается с частотой около 5200 оборотов в минуту (менее 90 оборотов в секунду).
Из-за этого частота вращения макроскопических объектов редко превышает тысячу оборотов в секунду. Например, частота вала газогенератора двигателя PW207K вертолета «Ансат» может достигать 60000 оборотов в минуту (1000 оборотов в секунду), а турбина двигателя CFM56, который устанавливается на самолетах фирм Boeing и Airbus, вращается с частотой около 5200 оборотов в минуту (менее 90 оборотов в секунду).
Уменьшая размеры объекта, можно заставить его вращаться гораздо быстрее. Оказывается, что для достижения сверхвысоких скоростей удобнее всего использовать частицы размером порядка ста нанометров, подвешенные в воздухе с помощью лазерного излучения (так называемая оптическая ловушка). Направляя на связанную частицу свет с круговой поляризацией, можно передать ей угловой момент и увеличить ее угловую скорость (эффект Садовского). Таким образом можно избежать механического трения, которое поглощает энергию и мешает разгонять частицу, а также контролировать центр вращения с точностью, сравнимой с теоретическим пределом.
К сожалению, на высоких скоростях начинает сказываться трение наночастицы о воздух, которое также уносит энергию частицы. Бороться с этим трением можно только откачивая установку до сверхнизких давлений, создавая в ней вакуум. Из-за подобных технических сложностей ученым не удавалось достичь в лаборатории скоростей вращения, превышающих по порядку десяти мегагерц. В новых работах ученым удалось преодолеть это препятствие, подтвердить теоретические предсказания и достичь частоты вращения порядка одного гигагерца.
Схема установок, в которой ученые разгоняют наночастицы до сверхвысоких угловых скоростей
René Reimann et al. / Phys. Rev. Lett.
Первая группа исследователей под руководством Лукаса Новотного (Lukas Novotny), использовала в качестве «спиннера» частицу кремнезема (проще говоря, обычного стекла) приближенно сферической формы и диаметром около ста нанометров. Для уменьшения потерь физики откачали установку до давления порядка 10−8 атмосфер и увеличили длину волны лазера, который использовался для разгона частицы, до 1565 нанометров. Это позволило уменьшить скорость нагрева частицы — в предыдущих экспериментах такой нагрев заставлял частицу «выскакивать» из ловушки и мешал разогнать ее выше определенного предела.
Для уменьшения потерь физики откачали установку до давления порядка 10−8 атмосфер и увеличили длину волны лазера, который использовался для разгона частицы, до 1565 нанометров. Это позволило уменьшить скорость нагрева частицы — в предыдущих экспериментах такой нагрев заставлял частицу «выскакивать» из ловушки и мешал разогнать ее выше определенного предела.
В результате ученые обнаружили, что с уменьшением давления при фиксированной мощности лазера и увеличении мощности при фиксированном давлении угловая скорость вращения частицы линейно растет, причем экспериментальная зависимость хорошо согласуется с теорией. Максимальная частота, полученная в этом эксперименте, достигала 1,03 гигагерц, что отвечало скорость краев частицы порядка 300 метров в секунду, центробежному ускорению порядка 1012 метров на секунду в квадрате и напряжению порядка 0,2 гигапаскаль. Для сравнения, критическое напряжение, при котором частица кремнезема разрывается, составляет примерно 10 гигапаскаль.
Зависимость частоты вращения наночастицы от давления при фиксированной мощности лазера
René Reimann et al. / Phys. Rev. Lett.
Зависимость частоты вращения наночастицы от мощности лазера при фиксированном давлении
René Reimann et al. / Phys. Rev. Lett.
Вторая группа, под руководством Тунцана Ли (Tongcang Li), заставляла вращаться наногантели — связанные друг с другом частицы кремнезема. Чтобы изготовить такие гантели, ученые «растворяли» наночастицы кремнезема в воде и получали коллоидную суспензию, а затем с помощью ультразвукового небулайзера заставляли воду формировать микрометровые капли, взвешенные в воздухе.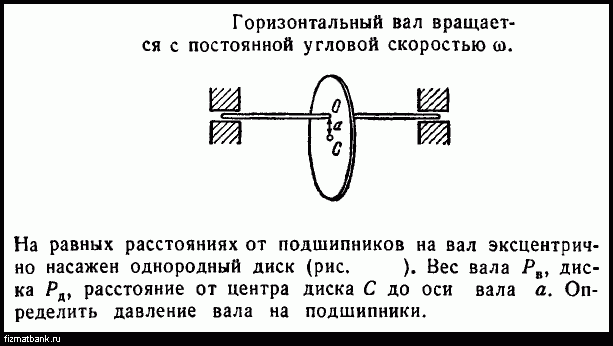 В некоторых из капель находилось две сферические частицы кремнезема; после испарения воды частицы оставались связаны в наногантели, которые ученые использовали в дальнейших опытах. Отношение диаметра шаров к расстоянию между ними для всех полученных наногантелей было примерно равно двум.
В некоторых из капель находилось две сферические частицы кремнезема; после испарения воды частицы оставались связаны в наногантели, которые ученые использовали в дальнейших опытах. Отношение диаметра шаров к расстоянию между ними для всех полученных наногантелей было примерно равно двум.
Фотографии нангантелей, полученные с помощью сканирующего электронного микроскопа
Jonghoon Ahn et al. / Phys. Rev. Lett.
Зависимость частоты вращения наногантели от давления при фиксированной мощности лазера
Jonghoon Ahn et al. / Phys. Rev. Lett.
Так же как и группа швейцарских ученых, группа под руководством Тунцана Ли помещала наногантели в оптическую ловушку, откачивала установку до давления порядка 10−7 атмосфер и светила на частицы лазером с круговой поляризацией и длиной волны около 1550 нанометров. Аналогично швейцарцам, физики получили, что скорость вращения линейно растет при уменьшении давления, а предельная частота вращения в этом случае составила примерно 1,1 гигагерц — при бо́льших скоростях гантель разрывалась под действием центробежной силы.
Аналогично швейцарцам, физики получили, что скорость вращения линейно растет при уменьшении давления, а предельная частота вращения в этом случае составила примерно 1,1 гигагерц — при бо́льших скоростях гантель разрывалась под действием центробежной силы.
Тем не менее, конструкция установки, аналогичная опыту Кавендиша, в котором проволока крутильных весов заменена на лазерное излучение, позволяет провести на ней качественно другие эксперименты. Если заменить в ней свет с круговой поляризацией на линейно поляризованный свет, наногантели будут колебаться, а не крутиться, что позволит в будущем измерить вращательный эффект Казимира (Casimir torque) и исследовать природу квантовой гравитации.
Впрочем, ученые признаются, что изначально они не ставили перед собой практических целей. Например, соавтор первой работы, Рене Рейманн (René Reimann), говорит: «Если честно, это просто было очень круто — иметь механический объект с самой высокой скоростью вращения в мире прямо перед нами». Тем не менее, работа ученых может пригодиться при изучении межзвездной пыли и вакуумного трения, исследовании поведения материалов и взаимосвязи между вращательными и поступательными степенями свободы в экстремальных условиях.
Тем не менее, работа ученых может пригодиться при изучении межзвездной пыли и вакуумного трения, исследовании поведения материалов и взаимосвязи между вращательными и поступательными степенями свободы в экстремальных условиях.
В ноябре прошлого года американские исследователи-нанотехнологи изготовили с помощью фотолитографии самый маленький в мире фиджет-спиннер, размер которого составил примерно сто микрометров.
Дмитрий Трунин
Основы углового ускорения и вращательного момента инерции
Угловое ускорение и момент инерции в конструкции машин Как поставщик гибких приводных муфт и предохранительных муфт с шариковой фиксацией нас часто просят оказать небольшую помощь в расчете крутящих моментов, особенно для клиентов, желающих модернизировать существующее оборудование.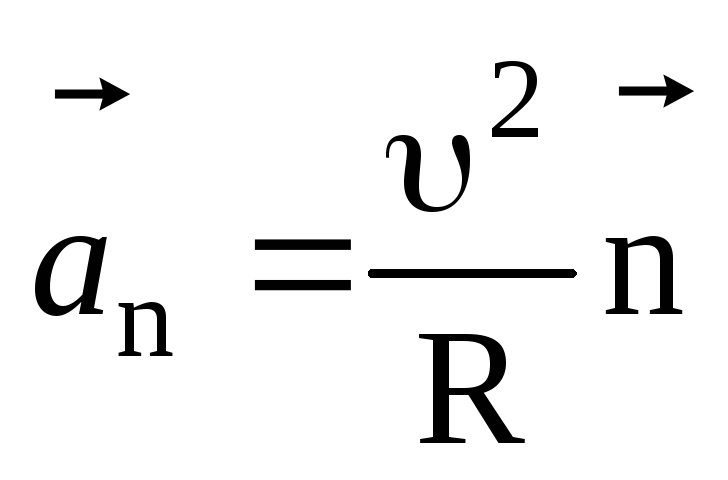 Чтобы помочь в процессе оценки крутящих моментов, мы рассмотрим один из основных расчетов, используемых для оценки крутящего момента, необходимого для ускорения вращающейся массы до определенной скорости в течение заданного времени.2). Уравнение ниже определяет скорость изменения угловой скорости.
Чтобы помочь в процессе оценки крутящих моментов, мы рассмотрим один из основных расчетов, используемых для оценки крутящего момента, необходимого для ускорения вращающейся массы до определенной скорости в течение заданного времени.2). Уравнение ниже определяет скорость изменения угловой скорости.
ω = угловая скорость в стандартной системе СИ, радиан в секунду (рад / сек), 1 радиан = 57,3 градуса
t = время разгона в секундах
π = 3,1416
n = скорость привода в оборотах в минуту об / мин
В следующем примере угловая скорость будет рассчитана для ускорения от 0 до 60 об / мин за одну секунду. Обратите внимание, что 2π радиан в секунду = 60 об / мин.
Этот расчет очень полезен при проектировании машин, потому что угловое ускорение, умноженное на крутящий момент инерции, равняется крутящему моменту. Имейте в виду, что точный момент инерции может быть трудно вычислить на основе сложной геометрии реальных приводных линий, а другие переменные, такие как трение, не учитываются в следующем расчете. Тем не менее, он по-прежнему очень полезен при приближении требований к крутящему моменту или установлении минимальных базовых значений для определения размеров компонентов.
Тем не менее, он по-прежнему очень полезен при приближении требований к крутящему моменту или установлении минимальных базовых значений для определения размеров компонентов.
Дж = момент инерции в кг ∙ м 2
T = крутящий момент в Н ∙ м
N = сила в Ньютонах
кг = масса в килограммах
м = радиус плеча рычага в метрах
В последнем примере ниже мы будем использовать найденное выше угловое ускорение для расчета крутящего момента на маховике с радиусом 1 метр и массой 1000 кг.
Как мы видим, если бы маховик с радиусом 1 метр и массой 1000 кг разогнался до 60 об / мин за одну секунду, для этого потребовалось бы 3141.59 Ньютон-метров входного крутящего момента.
Надеюсь, этот обзор по вычислению углового ускорения оказался для вас полезным. Если у вас есть вопросы, касающиеся выбора размеров и применения муфт вала или предохранительных муфт, обращайтесь в наш технический отдел.
Угол поворота и угловая скорость
Цели обучения
К концу этого раздела вы сможете:
- Определите длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Вычислить угловую скорость вращения колеса автомобиля.
В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой.Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на рисунке 1 вращается вокруг своего центра — каждая точка в объекте движется по дуге окружности.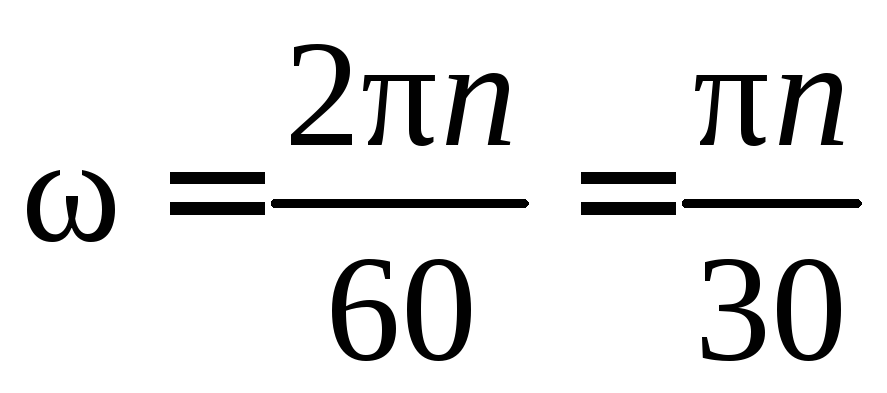 Рассмотрим линию от центра компакт-диска до его края. Каждая яма , , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию.Мы определяем угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [latex] \ displaystyle \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [ / латекс]
Рассмотрим линию от центра компакт-диска до его края. Каждая яма , , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию.Мы определяем угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [latex] \ displaystyle \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [ / латекс]
Рис. 1. Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ за время Δt .
Рис. 2. Радиус круга повернут на угол Δθ . Длина дуги Δs описана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории, как показано на Рисунке 2. Обратите внимание, что r — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r . Окружность круга равна 2π r . Таким образом, за один полный оборот угол поворота составляет
Окружность круга равна 2π r . Таким образом, за один полный оборот угол поворота составляет
[латекс] \ displaystyle \ Delta \ theta = \ frac {2 \ pi {r}} {r} = 2 \ pi \\ [/ latex].
Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ , чтобы быть радиан (рад), определенным так, что 2π рад = 1 оборот.
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.
| Таблица 1. Сравнение угловых единиц | |
|---|---|
| Градус Меры | Радианная мера |
| 30º | [латекс] \ displaystyle \ frac {\ pi} {6} \\ [/ latex] |
| 60º | [латекс] \ displaystyle \ frac {\ pi} {3} \\ [/ latex] |
| 90º | [латекс] \ displaystyle \ frac {\ pi} {2} \\ [/ latex] |
| 120º | [латекс] \ displaystyle \ frac {2 \ pi} {3} \\ [/ latex] |
| 135º | [латекс] \ displaystyle \ frac {3 \ pi} {4} \\ [/ latex] |
| 180º | π |
Рисунок 3. {\ circ}} {2 \ pi} \ приблизительно 57.{\ circ} \\ [/ латекс].
{\ circ}} {2 \ pi} \ приблизительно 57.{\ circ} \\ [/ латекс].
Угловая скорость
Насколько быстро вращается объект? Определим угловую скорость ω как скорость изменения угла. В символах это [латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta {t}} \\ [/ latex], где угловой поворот Δ θ происходит за время Δ t . Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω аналогична линейной скорости v . Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги Δ с за время Δ t , поэтому она имеет линейную скорость [латекс] v = \ frac {\ Delta {s}} {\ Delta {t}} \\ [/ латекс].
Из [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex] мы видим, что Δ s = r Δ θ . Подставляя это в выражение для v , получаем [latex] v = \ frac {r \ Delta \ theta} {\ Delta {t}} = r \ omega \\ [/ latex].
Подставляя это в выражение для v , получаем [latex] v = \ frac {r \ Delta \ theta} {\ Delta {t}} = r \ omega \\ [/ latex].
Мы записываем эту связь двумя разными способами и получаем два разных вывода:
[латекс] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex].
Первое соотношение в [latex] v = r \ omega \ text {or} \ omega \ frac {v} {r} \\ [/ latex] гласит, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (наибольшее r ), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью .Вторую взаимосвязь в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины такая же, как скорость v автомобиля. См. Рисунок 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой v означает большой ω , потому что v = rω . Точно так же шина с большим радиусом, вращающаяся с той же угловой скоростью ( ω ), будет создавать для автомобиля большую линейную скорость ( v ).
Точно так же шина с большим радиусом, вращающаяся с той же угловой скоростью ( ω ), будет создавать для автомобиля большую линейную скорость ( v ).
Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси составляет v , как если бы автомобиль был поднят. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.
Пример 1. Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость 0.Автомобильная шина радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 4.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем v = 15,0 м / с. Радиус шины задан равным r = 0,300 м. Зная v и r , мы можем использовать второе соотношение в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] для вычисления угловой скорости .
Решение
Для вычисления угловой скорости мы будем использовать следующее соотношение: [latex] \ omega \ frac {v} {r} \\ [/ latex].
Подстановка известных,
[латекс] \ omega = \ frac {15.0 \ text {m / s}} {0.300 \ text {m}} = 50.0 \ text {rad / s} \\ [/ latex].
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если землеройный комбайн с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его колеса вращались медленнее. У них будет угловая скорость [latex] \ omega = \ frac {15.0 \ text {m / s}} {1.20 \ text {m}} = 12.5 \ text {rad / s} \\ [/ latex].
И ω , и v имеют направления (следовательно, это угловая и линейная скорости , соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.
Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.
Эксперимент на вынос
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5.Когда объект движется по кругу, например, муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.
Исследования PhET: Ladybug Revolution
Присоединяйтесь к божьей коровке в исследовании вращательного движения. {\ circ} = 1 \ text { революция} \\ [/ латекс].{\ circ} \\ [/ латекс].
{\ circ} = 1 \ text { революция} \\ [/ латекс].{\ circ} \\ [/ латекс].
Концептуальные вопросы
- Есть аналогия между вращательными и линейными физическими величинами.Какие вращательные величины аналогичны расстоянию и скорости?
Задачи и упражнения
- У полуприцепов счетчик пробега на одной ступице колеса прицепа. Ступица утяжеляется так, что она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние. Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
- Микроволновые печи вращаются со скоростью около 6 об / мин.
 6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли? - Бейсбольный питчер выносит руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера составляет 35,0 м / с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
- В лакроссе мяч выбрасывается из сетки на конце клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча около локтевого сустава равна 30.0 рад / с и мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
- Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
- Комплексные концепции. При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава. (а) Если скорость кончика ботинка кикера составляет 35,0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика ботинка, какова угловая скорость кончика ботинка? (b) Башмак находится в контакте с изначально неподвижным 0.
 Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность действия футбольного мяча, пренебрегая сопротивлением воздуха.
Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность действия футбольного мяча, пренебрегая сопротивлением воздуха. - Постройте свою проблему. Рассмотрим аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками. Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению.Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную диаграмму тела одного всадника. Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной.
Глоссарий
Длина дуги: Δ с , расстояние, пройденное объектом по круговой траектории
яма: крошечная выемка на спиральной дорожке, отформованной в верхней части слоя поликарбоната CD
угол поворота: отношение длины дуги к радиусу кривизны на круговой траектории: [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex]
радиус кривизны: радиус круговой траектории
радиан: единица измерения угла
угловая скорость: ω, скорость изменения угла, под которым объект движется по круговой траектории
Избранные решения проблем и упражнения
1. 723 км
723 км
3. 5 × 10 7 оборотов
5. 117 рад / с
7. 76,2 рад / с; 728 об / мин
8. (а) 33,3 рад / с; (б) 500 Н; (в) 40,8 м
Как рассчитать угловую скорость
Обновлено 15 декабря 2020 г.
Кевин Бек
В повседневном дискурсе «скорость» и «скорость» часто используются как синонимы. Однако в физике эти термины имеют особые и различные значения. «Скорость» — это скорость перемещения объекта в пространстве, и она задается только числом с определенными единицами измерения (часто в метрах в секунду или милях в час).С другой стороны, скорость — это скорость, связанная с направлением. Таким образом, скорость называется скалярной величиной, тогда как скорость — векторной величиной.
Когда машина мчится по шоссе или бейсбольный мяч проносится по воздуху, скорость этих объектов измеряется относительно земли, тогда как скорость включает больше информации. Например, если вы едете в машине со скоростью 70 миль в час по межштатной автомагистрали 95 на восточном побережье Соединенных Штатов, также полезно знать, идет ли она на северо-восток в сторону Бостона или на юг в сторону Флориды. В случае с бейсбольным мячом вы можете захотеть узнать, изменяется ли его координата y быстрее, чем координата x (летающий мяч), или верно ли обратное (линейный привод). Но как насчет вращения шин или вращения (вращения) бейсбольного мяча, когда машина и мяч движутся к своей конечной цели? Для такого рода вопросов физика предлагает концепцию угловой скорости .
В случае с бейсбольным мячом вы можете захотеть узнать, изменяется ли его координата y быстрее, чем координата x (летающий мяч), или верно ли обратное (линейный привод). Но как насчет вращения шин или вращения (вращения) бейсбольного мяча, когда машина и мяч движутся к своей конечной цели? Для такого рода вопросов физика предлагает концепцию угловой скорости .
Основы движения
Вещи перемещаются в трехмерном физическом пространстве двумя основными способами: перемещением и вращением.Трансляция — это перемещение всего объекта из одного места в другое, как машина, едущая из Нью-Йорка в Лос-Анджелес. С другой стороны, вращение — это циклическое движение объекта вокруг фиксированной точки. Многие объекты, такие как бейсбольный мяч в приведенном выше примере, демонстрируют оба типа движения одновременно; По мере того, как летающий мяч перемещается по воздуху от домашней пластины к дальнему забору, он также вращается с заданной скоростью вокруг своего центра.
Описание этих двух видов движения рассматривается как отдельные физические задачи; то есть при расчете расстояния, которое мяч проходит по воздуху, на основе таких вещей, как начальный угол запуска и скорость, с которой он покидает летучую мышь, вы можете игнорировать его вращение, а при вычислении его вращения вы можете рассматривать его как сидящего в одном место для настоящих целей.
Уравнение угловой скорости
Во-первых, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-то другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругам или их частям. . Вы можете вспомнить из геометрии или тригонометрии, что длина окружности равна его диаметру, умноженному на константу пи, или πd . (Значение пи составляет около 3,14159.) Это чаще всего выражается в терминах радиуса окружности r , который составляет половину диаметра, в результате чего длина окружности 2πr .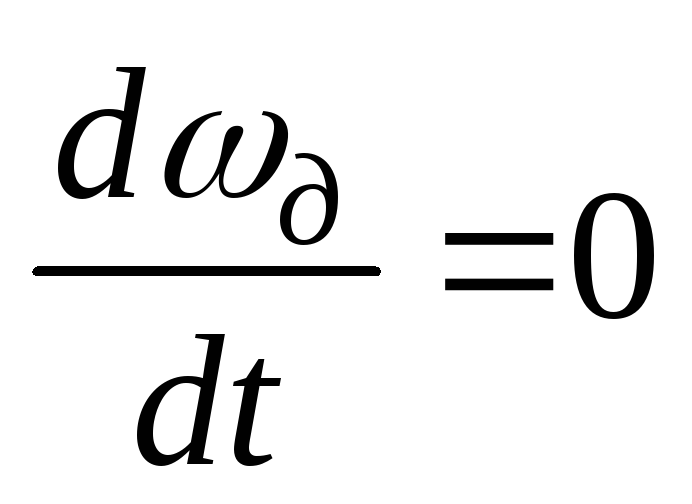 o} {2 \ pi} = 57.o
o} {2 \ pi} = 57.o
В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно в секунду.
Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r от центра круга, причем направление v всегда перпендикулярно радиус круга, то угловая скорость может быть записана в виде
\ omega = \ frac {v} {r}
, где ω — греческая буква омега.Единицы угловой скорости — радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v / r дает м / с, деленные на м, или с -1 , что означает, что радианы технически являются безразмерной величиной.
Уравнения вращательного движения
Формула углового ускорения выводится таким же существенным образом, как и формула угловой скорости: это просто линейное ускорение в направлении, перпендикулярном радиусу окружности (эквивалентно его ускорению по касательной к круговой путь в любой точке), деленный на радиус круга или части круга, который равен:
\ alpha = \ frac {\ omega} {t}
, потому что для кругового движения:
a_t = \ frac { \ omega r} {t} = \ frac {v} {t}
α , как вы, наверное, знаете, это греческая буква «альфа». 2} {r}
2} {r}
Это ускорение направлено к точке, вокруг которой вращается рассматриваемый объект. Это может показаться странным, так как объект не приближается к этой центральной точке, поскольку радиус r фиксирован. Думайте о центростремительном ускорении как о свободном падении, при котором нет опасности столкновения объекта с землей, потому что сила, притягивающая объект к нему (обычно сила тяжести), точно компенсируется тангенциальным (линейным) ускорением, описываемым первым уравнением в эта секция.Если бы a c не было равно a t , объект либо улетел бы в космос, либо вскоре врезался бы в середину круга.
Связанные величины и выражения
Хотя угловая скорость обычно выражается, как отмечалось, в радианах в секунду, могут быть случаи, в которых предпочтительнее или необходимо использовать вместо этого градусы в секунду или, наоборот, преобразовывать градусы в радианы. перед решением проблемы.
перед решением проблемы.
Допустим, вам сказали, что источник света вращается на 90 ° каждую секунду с постоянной скоростью.Какова его угловая скорость в радианах?
Сначала запомните, что 2π радиан = 360 °, и установите пропорцию:
\ frac {360} {2 \ pi} = \ frac {90} {\ omega} \ подразумевает 360 \ omega = 180 \ pi \ подразумевает \ omega = \ frac {\ pi} {2}
Ответ — половина пи радиан в секунду.
Если бы вам дополнительно сказали, что световой луч имеет дальность действия 10 метров, то какова будет вершина линейной скорости луча v , его угловое ускорение α и его центростремительное ускорение a с ?
Чтобы решить для v , сверху, v = ωr, где ω = π / 2 и r = 10m:
\ frac {\ pi} {2} 10 = 15.2
Угловая скорость в сравнении с линейной скоростью
Опираясь на предыдущую задачу, представьте себя на очень большой карусели с маловероятным радиусом 10 километров (10 000 метров). Эта карусель совершает один полный оборот каждые 1 минуту 40 секунд или каждые 100 секунд.
Эта карусель совершает один полный оборот каждые 1 минуту 40 секунд или каждые 100 секунд.
Одним из следствий разницы между угловой скоростью, которая не зависит от расстояния от оси вращения, и линейной круговой скоростью, которой нет, является то, что два человека, испытывающие одинаковые ω , могут испытывать совершенно разные физические ощущения. .Если вы окажетесь на расстоянии 1 метра от центра в этой предполагаемой массивной карусели, ваша линейная (тангенциальная) скорость будет:
v_t = \ omega r = \ frac {2 \ pi} {100} (1) = 0,0628 \ text {м / с}
или 6,29 см (менее 3 дюймов) в секунду.
Но если вы находитесь на краю этого монстра, ваша линейная скорость будет:
v_t = \ omega r = \ frac {2 \ pi} {100} (10000) = 628 \ text {m / s}
Это примерно 1406 миль в час, быстрее, чем пуля. Подожди!
Выполненная работа и переданная мощность
Выполненная работа
Выполненная работа — это сила, умноженная на расстояние, перемещенное на силу , и может быть выражена как
W = F s (1)
где
W = выполненная работа (Дж, Нм)
F = сила (Н)
s = расстояние, перемещаемое силой (с)
Для углового перемещения
работа done может быть выражено как
W = F θ r
= T θ (2)
где
W = работа (Джоули)
θ559 (радианы)
r = радиус (м)
T = крутящий момент или момент (Нм)
Передаваемая мощность
Мощность — это соотношение между n выполненная работа и затраченное время могут быть выражены как
P = W / dt
= T θ / dt
= T ω
= 2 π n T
= 2 π (n об / мин /60) T
= 0.
105 n об / мин T (3)
где
P = мощность (Вт)
dt = затраченное время (с)
ω = 2θ / dt π n = угловая скорость (рад / с)
n = скорость (об / с)
n об / мин = скорость (об / мин, об / мин)
Примечание! — машина должна вращаться, чтобы производить энергию! Машина без вращения может передавать крутящий момент, как электродвигатель, но поскольку расстояние не перемещается силой, мощность не производится.Как только машина начинает вращаться, вырабатывается мощность.
Пример — требуемый крутящий момент для выработки мощности
Машина вращается со скоростью 3000 об / мин (об / мин) и потребляет 5 кВт . Крутящий момент на валу можно рассчитать, изменив (3) на
T = P / 2 π n
= (5 кВт) (1000 Вт / кВт) / 2 π (3000 об / мин) / (60 сек / мин)
= 15,9 Нм
Угловая скорость: определение, формула и примеры — видео и стенограмма урока
Радианы
Перед тем, как перейти к угловой скорости, нам нужно рассмотреть еще одну вещь, а именно радианы. Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой. Техническое определение радиан. Измерение — это длина дуги, образуемой углом, деленная на радиус круга, частью которого является угол, где «подтянутый» означает быть противоположным углу и продолжаться от одной точки круг к другому, оба отмечены углом. Это говорит нам о том, что угол тета = с / r радиан, где с = длина дуги, соответствующей тета, и r = радиус круга, частью которого является тета.
Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой. Техническое определение радиан. Измерение — это длина дуги, образуемой углом, деленная на радиус круга, частью которого является угол, где «подтянутый» означает быть противоположным углу и продолжаться от одной точки круг к другому, оба отмечены углом. Это говорит нам о том, что угол тета = с / r радиан, где с = длина дуги, соответствующей тета, и r = радиус круга, частью которого является тета.
Поскольку большинству из нас удобно измерять углы в градусах, удобно, что мы можем легко преобразовать градус в радиан, умножив градус на пи / 180. Например, угол в 45 градусов имеет радиан. мера 45 (пи / 180), что равно пи / 4 радиана.
Угловая скорость
Угловая скорость встречается реже, чем линейная скорость, поскольку она применяется только к объектам, движущимся по круговой траектории.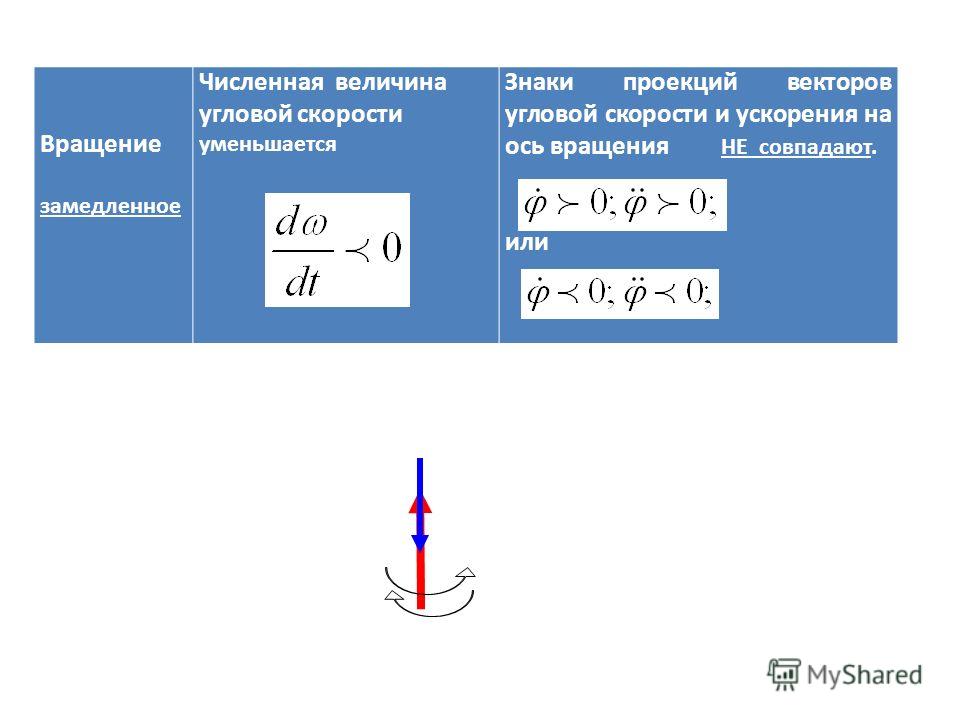 Например, гоночный автомобиль на круговой трассе, шар рулетки на колесе рулетки или колесо обозрения — все они имеют угловую скорость.
Например, гоночный автомобиль на круговой трассе, шар рулетки на колесе рулетки или колесо обозрения — все они имеют угловую скорость.
Угловая скорость объекта — это угловое смещение объекта во времени. Когда объект движется по круговой траектории, центральный угол, соответствующий положению объекта на круге, изменяется. Угловая скорость, представленная как w , представляет собой скорость изменения этого угла во времени.
Например, колесо обозрения может вращать пи / 6 радиан каждую минуту. Следовательно, угловая скорость колеса обозрения будет равна пи / 6 радиан в минуту.
Формулы угловой скорости
Есть три формулы , которые мы можем использовать, чтобы найти угловую скорость.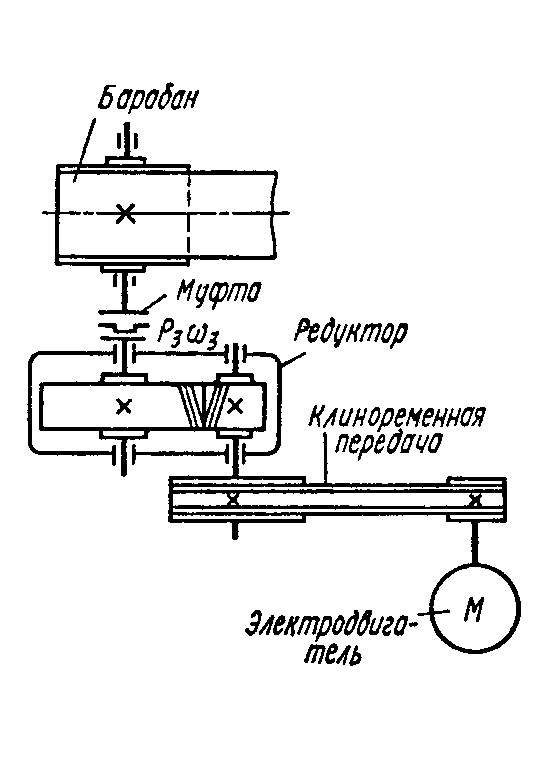
Вариант 1
Первое вытекает прямо из определения.Угловая скорость — это скорость изменения позиционного угла объекта во времени, поэтому w = theta / t , где w = угловая скорость, theta = позиционный угол и t = время.
Например, если гоночный автомобиль движется по круговой трассе и проходит 1 круг или 2 радиана на дюйм за 4 минуты, то мы можем определить угловую скорость автомобиля, подставив theta = 2pi радиан и t = 4 минуты в наша формула, чтобы получить w = 2pi / 4 = pi / 2 радиан в минуту.Угловая скорость автомобиля составляет пи / 2 радиана в минуту.
Вариант 2
Чтобы получить нашу вторую формулу для угловой скорости, мы понимаем, что тета дана в радианах, а определение радианной меры дает theta = с / r . Таким образом, мы можем подставить theta = s / r в нашу первую формулу угловой скорости.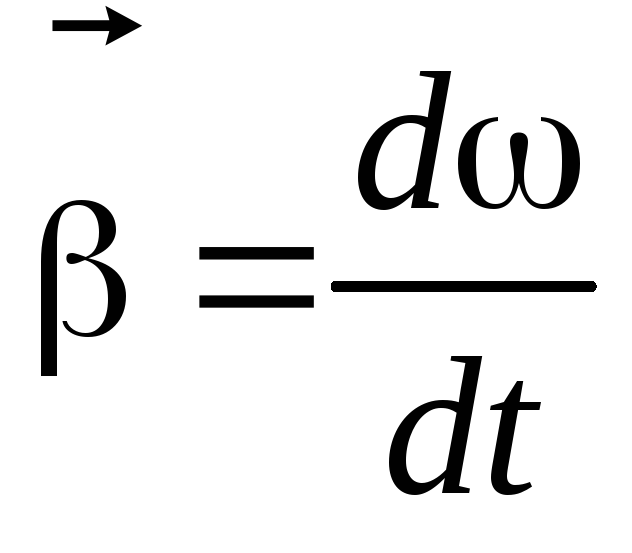 Это дает w = ( s / r ) / t . Упрощение дает w = s / ( r t ), где s = длина дуги, r = радиус и t = время.
Это дает w = ( s / r ) / t . Упрощение дает w = s / ( r t ), где s = длина дуги, r = радиус и t = время.
Например, если колесо рулетки имеет радиус 10 дюймов, а шарик проходит 7 дюймов по круговой траектории за 2 секунды, то мы можем определить угловую скорость шара, вставив s = 7 дюймов, r = 10 дюймов и t = 2 секунды на w = s / ( r t ), чтобы получить w = 7 / (10 * 2) = 0,35 радиан в секунду. Угловая скорость мяча составляет 0,35 радиана в секунду.
Вариант 3
Последняя формула исходит из признания того, что мы можем переписать нашу вторую формулу угловой скорости как w = с / ( r t ) = ( s / t ) (1/ r ).Напомним, что s / t — наша линейная скорость, поэтому мы можем переписать эту формулу как w = v (1/ r ) = v / r , где v = linear скорость и r = радиус круга.
Например, если гоночный автомобиль движется по круговой трассе со скоростью 110 миль в час, а радиус гоночной трассы составляет 0,2 мили, то мы можем найти угловую скорость автомобиля, подключив v = 110 миль в час и r = 0.2 мили в нашу формулу, чтобы получить w = 110 / 0,2 = 550 радиан в час.
Резюме урока
Мы рассмотрели линейную скорость, , скорость изменения положения объекта, движущегося по прямой линии, относительно времени и радиан, мера угла (тета = с / r , где s = длина дуги и r = радиус). Мы видели, что оба они играют важную роль в угловой скорости. Угловая скорость — это угловое смещение во времени объекта или частицы, которые движутся по круговой траектории.У нас есть три формулы, которые мы используем для определения угловой скорости, и они отображаются на экране.
Эти формулы и определения снабдили нас всем необходимым для эффективной и действенной работы с угловой скоростью.
Карта механики — Системы с ременным и зубчатым приводом
Ременные и шкивные системы, а также системы с шестеренчатым приводом представляют собой обычные способы передачи вращательного движения и крутящего момента с одного вала на другой.Ремни обеспечивают гибкость в том, что валы не обязательно должны находиться рядом друг с другом, а шестерни чаще используются в приложениях с высокими нагрузками.
| Ремни и шкивы часто используются для передачи движения и крутящего момента от одного вала к другому. | Шестерни — еще один распространенный способ передачи движения и крутящего момента от одного вала к другому. |
Положение, скорость и ускорение в системах с ременным приводом
На схеме ниже показана простая система с ременным приводом.Шкив A и шкив B имеют свой собственный радиус и соединены ремнем, который, как мы предполагаем, не проскальзывает относительно шкивов. Каждый шкив совершает вращение с фиксированной осью и поэтому будет следовать этим кинематическим правилам отдельно, однако движение ремня можно использовать для связи движения двух шкивов.
В качестве ограничения мы можем предположить, что скорость шкива будет одинаковой по всей петле в любой момент времени.Если бы это было не так, то в одних местах пояс собирался, а в других растягивался. Если ремень не проскальзывает, скорость ремня будет такой же, как скорость кромки каждого из двух шкивов. Уравнивая эти две скорости друг другу и работая в обратном направлении, чтобы связать их с угловыми скоростями, мы получаем среднее уравнение ниже. Взятие интеграла или производной позволяет нам также связать угловые смещения или угловые ускорения с аналогичными уравнениями.
| Угловые перемещения: | \ [r_ {A} (\ Delta \ Theta _ {A}) = r_ {B} (\ Delta \ Theta_ {B}) \] |
|---|---|
| Угловые скорости: | \ [r_ {A} \ omega_ {A} = r_ {B} \ omega_ {B} \] |
| Угловые ускорения: | \ [r_ {A} \ alpha_ {A} = r_ {B} \ alpha_ {B} \] |
Если у нас есть более сложная серия ремней и шкивов, мы будем анализировать систему поэтапно. Сюда входят шкивы, соединенные ремнями, как у нас выше, а также шкивы, соединенные через вал, как показано со шкивами B и C на схеме ниже.
Сюда входят шкивы, соединенные ремнями, как у нас выше, а также шкивы, соединенные через вал, как показано со шкивами B и C на схеме ниже.
Для шкивов на одном валу угловые смещения, угловые скорости и угловые ускорения будут одинаковыми.
| \ [\ Delta \ Theta_ {B} = \ Delta \ Theta_ {C} \] | \ [\ omega_ {B} = \ omega_ {C} \] | \ [\ alpha_ {B} = \ alpha_ {C} \] |
Если мы знаем угловое смещение, угловую скорость или угловое ускорение шкива A, мы могли бы найти угловое смещение, угловую скорость или угловое ускорение шкива D, перемещая одно взаимодействие за раз (определение движения шкива B, затем C, затем D).
Положение, скорость и ускорение в зубчатых передачах
На схеме ниже показана простая зубчатая передача.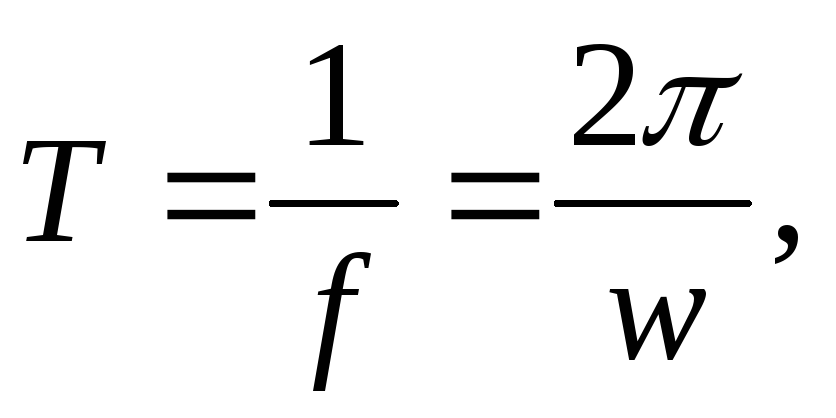 Gear A и Gear B имеют свой собственный радиус и взаимодействуют в точке контакта. Каждая шестерня совершает вращение с фиксированной осью и поэтому будет следовать этим кинематическим правилам отдельно, однако движение зубьев в точке контакта можно использовать для соотнесения движения одной шестерни с другой.
Gear A и Gear B имеют свой собственный радиус и взаимодействуют в точке контакта. Каждая шестерня совершает вращение с фиксированной осью и поэтому будет следовать этим кинематическим правилам отдельно, однако движение зубьев в точке контакта можно использовать для соотнесения движения одной шестерни с другой.
В качестве ограничения мы можем предположить, что скорость зубьев в точке контакта будет такой же. Если бы это было не так, зубья одной шестерни проходили бы сквозь зубцы другой шестерни. Приравнивая эти две скорости друг к другу и работая в обратном направлении, чтобы связать угловые скорости, мы находим второе уравнение ниже. Взятие интеграла или производной позволяет нам также связать угловые смещения или угловые ускорения с аналогичными уравнениями.
| Угловые перемещения: | \ [r_ {A} (\ Delta \ Theta _ {A}) = — r_ {B} (\ Delta \ Theta_ {B}) \] |
|---|---|
| Угловые скорости: | \ [r_ {A} \ omega_ {A} = — r_ {B} \ omega_ {B} \] |
| Угловые ускорения: | \ [r_ {A} \ alpha_ {A} = — r_ {B} \ alpha_ {B} \] |
Вы заметите, что приведенные выше уравнения соответствуют уравнениям, которые мы имели для систем с ременным приводом, за исключением знака минус в правой части каждого уравнения. Это связано с тем, что зацепленные шестерни вращаются в противоположных направлениях (если одна шестерня вращается по часовой стрелке, другая будет вращаться против часовой стрелки), в то время как шкивы в системах с ременным приводом всегда вращаются в одном и том же направлении.
Это связано с тем, что зацепленные шестерни вращаются в противоположных направлениях (если одна шестерня вращается по часовой стрелке, другая будет вращаться против часовой стрелки), в то время как шкивы в системах с ременным приводом всегда вращаются в одном и том же направлении.
Также аналогично системам с ременным приводом, у нас могут быть составные зубчатые передачи с тремя или более шестернями, как показано на рисунке ниже. В этих сценариях у нас также, вероятно, будут шестерни, которые соединены через вал, например, синие и желтые шестерни, показанные ниже. В таких ситуациях шестерни на одном валу будут иметь совпадающие угловые смещения, угловые скорости и угловые ускорения.Как и в случае систем с ременным приводом, вам просто нужно переходить зубчатую передачу по одному шагу за раз, применяя правильный набор уравнений, чтобы соответствовать каждому шагу взаимодействия.
На анимированной диаграмме выше показана составная зубчатая передача. Красная и синяя шестерни взаимодействуют через зацепляющиеся зубья, затем синяя и желтая шестерни находятся на одном валу, затем, наконец, желтая и зеленая шестерни взаимодействуют через зацепляющиеся зубья.
Концепция, которая обычно используется в зубчатых передачах, которая обычно не используется в системах с ременным приводом, — это концепция передаточного числа .Для любой зубчатой передачи передаточное число определяется как угловая скорость входа, деленная на угловую скорость выхода. Основываясь на приведенных выше уравнениях, мы также можем доказать, что отношение угловых смещений или угловых ускорений будет аналогично передаточному отношению. Однако передаточное число всегда определяется как положительное число, поэтому вам все равно придется использовать интуицию, чтобы определить направление выходного сигнала.
| \ [Передаточное число = \ frac {\ omega_ {input}} {\ omega_ {output}} = \ frac {\ Delta \ Theta_ {input}} {\ Delta \ Theta_ {output}} = \ frac { \ alpha_ {input}} {\ alpha_ {output}} \] |
В простой двухступенчатой системе передаточное число будет равно радиусу выходной шестерни, деленному на радиус входной шестерни, или количеству зубьев ведомой шестерни, разделенному на количество зубьев на входная шестерня (так как количество зубьев будет прямо пропорционально радиусу).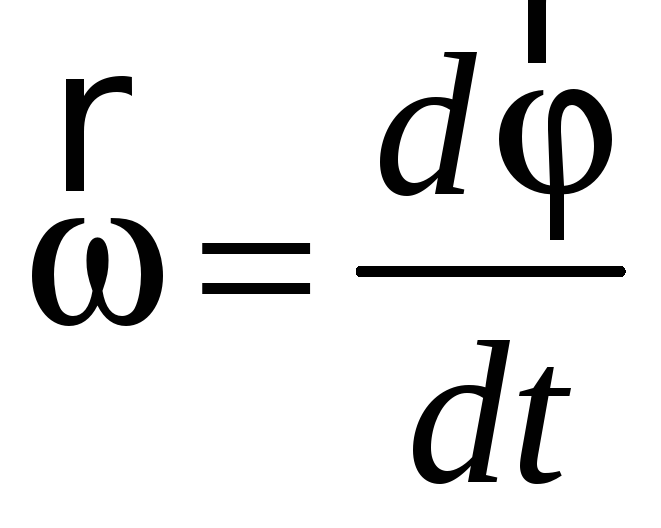 В составных зубчатых передачах этот простой расчет, приведенный ниже, не будет работать, но если вам задано передаточное число для составной зубчатой передачи, вы все равно можете применить приведенные выше уравнения.
В составных зубчатых передачах этот простой расчет, приведенный ниже, не будет работать, но если вам задано передаточное число для составной зубчатой передачи, вы все равно можете применить приведенные выше уравнения.
| \ [Передаточное число = \ frac {\ omega_ {input}} {\ omega_ {output}} = \ frac {r_ {output}} {r_ {input}} = \ frac {N_ {output}} { N_ {input}} \] |
Анализ крутящего момента маховика и вала | Инженеры Edge
Связанные ресурсы: механические станки
Анализ крутящего момента маховика и вала
Технический анализ
Проектирование и проектирование редукторов
Проектирование машин, уравнения и калькуляторы
Анализ крутящего момента маховика и вала
Маховик, установленный на относительно жестком валу, показан на рис.а. Учитывая равновесие моментов,
экв1
где,
T i = ведущий или входной крутящий момент (Н-м)
T o = нагрузка или выходной крутящий момент (Н-м)
I = момент инерции массы маховика (кг-м 2 )
ω = угловая скорость вала (рад / с) (dθ / dt)
Фиг. 1
1
Крутящий момент на валу маховика
Когда крутящий момент больше, чем крутящий момент нагрузки, член (T i — T o ) положительный, и маховик ускоряется.Когда крутящий момент меньше, чем крутящий момент нагрузки, термин (T i — T o ) отрицательный, указывая на замедление маховика. Диаграмма T -θ для конкретного приложения показана на рис. 2 (а). В этом случае мощность подается на машину от двигателя с постоянным крутящим моментом, развивающего крутящий момент Tm. Рабочий цикл ведомой машины состоит из трех частей — AB, BC и CD. Во время элементов AB и CD крутящий момент, необходимый машине, остается постоянным на уровне T 1 . В точке B он увеличивается до T 2 и остается постоянным в течение элемента BC.Цикл повторяется для каждого оборота.
Фиг.2
(а) Диаграмма крутящего момента, (б) Диаграмма скорости
Во время первого элемента AB крутящий момент, необходимый для машины, меньше крутящего момента, обеспечиваемого двигателем (T 1  Таким образом, маховик ускоряется, и его угловая скорость увеличивается до wmax. в точке B. Во время элемента BC крутящий момент, необходимый для машины, больше крутящего момента, передаваемого двигателем (T 2 > T м ).Маховик замедляется, и его угловая скорость уменьшается до wmin. в точке C. Это изменение угловой скорости показано на рис. 2 (б).
Таким образом, маховик ускоряется, и его угловая скорость увеличивается до wmax. в точке B. Во время элемента BC крутящий момент, необходимый для машины, больше крутящего момента, передаваемого двигателем (T 2 > T м ).Маховик замедляется, и его угловая скорость уменьшается до wmin. в точке C. Это изменение угловой скорости показано на рис. 2 (б).
В элементах AB и CD энергия подводится к маховику. Подводимая энергия U i определяется выражением,
экв 2
В элементе BC энергия снимается с маховика, а выход энергии U o от маховика определяется выражением,
экв. 3
Изменение кинетической энергии от точки B до C определяется как
экв 4
или
экв 5
Разница между максимальной и минимальной скоростями (ω макс. — w мин. ) во время цикла называется максимальным колебанием скорости. Отношение максимального колебания скорости к средней скорости называется коэффициентом колебания скорости. Следовательно, коэффициент колебания скорости, обозначенный C s , равен,
.экв.6
где ω — средняя или средняя угловая скорость маховика. Выдается,
экв.7
Подставляя уравнения (6) и (7) в выражение (a),
Значения коэффициентов колебания скорости, используемые на практике, приведены в таблице 1.Коэффициент колебания скорости можно выразить следующими способами:
или
Аналогично
или
или
где n — скорость в об / мин.
Иногда используется термин, называемый коэффициентом «устойчивости». Коэффициент устойчивости определяется как величина, обратная коэффициенту колебания скорости. Обозначается буквой м.
Следовательно,
Таблица 1, Коэффициенты колебаний скорости
| Тип оборудования | С с |
| Прессы для пробивки, резки и формовки | 0.200 |
| Компрессор (с ременным приводом) | 0,120 |
| Компрессор (шестеренчатый) | 0,020 |
| Станки | 0,025 |
| Поршневые насосы | 0,040 |
| Редукторные передачи | 0,020 |
| Двигатели внутреннего сгорания | 0.030 |
| Генераторы постоянного тока (прямой привод) | 0,010 |
| Генератор переменного тока (прямой привод) | 0,005 |
© Copyright 2000 — 2021, Engineers Edge, LLC www.
 Производим полный комплекс услуг по подбору редукторов, оказываем консультации для клиентов.
Производим полный комплекс услуг по подбору редукторов, оказываем консультации для клиентов.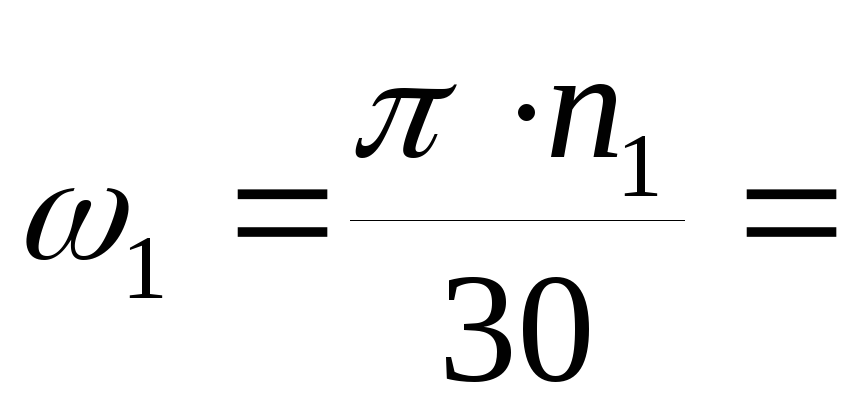 Оказываем полный комплекс услуг по разработке и производству.
Оказываем полный комплекс услуг по разработке и производству.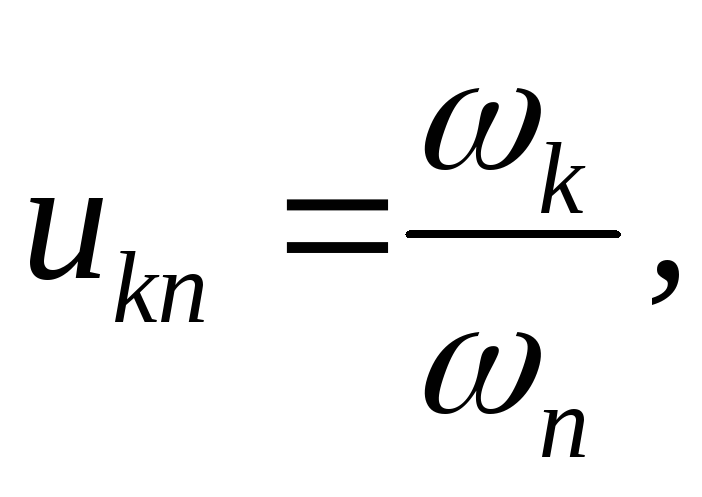

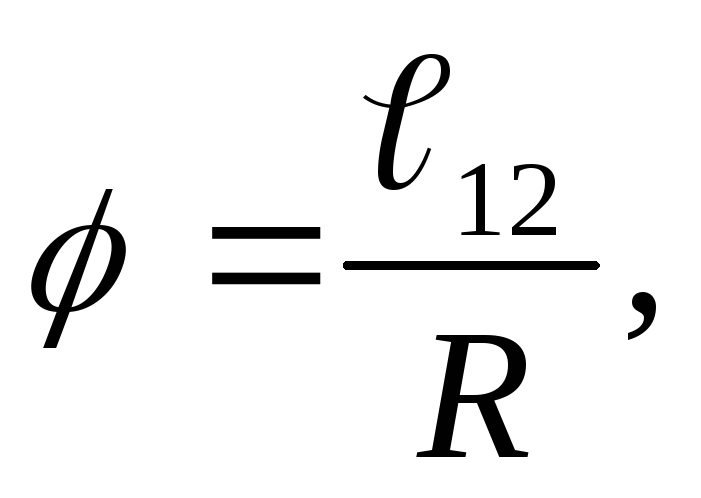 6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли? Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность действия футбольного мяча, пренебрегая сопротивлением воздуха.
Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность действия футбольного мяча, пренебрегая сопротивлением воздуха. 105 n об / мин T (3)
105 n об / мин T (3)