Остановка по четным и нечетным числам: Знак «Стоянка запрещена по четным или нечетным числам месяца»
Дорожный знак 3.29 «Стоянка запрещена по нечетным числам месяца»
Правила установки и принципы действия дорожных знаков «Стоянка запрещена по нечетным числам месяца» и «Стоянка запрещена по четным числам месяца» мало чем отличаются от знака-исходника — «Стоянка запрещена». Но необходимость в их наличии очевидна.
На узких участках дорог — в местах расположения многочисленных офисов учреждений и организаций, где большое количество транспортных средств осуществляет парковку, — возникает проблема затрудненного встречного разъезда.
Автомобили, стоящие по обеим сторонам дороги, сужают проезжую часть и делают встречное движение практически невозможным.
Судя по самому названию знаков, они запрещают стоянку по нечетным и четным числам месяца (соответственно). Иными словами, в зоне действия знака в конкретный день месяца запрещена только стоянка. Но, важно помнить, что остановка разрешается.
Зона действия знаков «Стоянка запрещена по нечетным числам месяца» и «Стоянка запрещена по четным числам месяца» начинается в месте их установки и продолжается до участков дороги, которые являются:
- Ближайшим по ходу следования перекрестком;
- Концом населенного пункта;
- Местом установки знака «Конец зоны всех ограничений».

Кроме того, данные дорожные знаки могут сочетаться с табличками 8.2.2 — 8.2.6. В этом случае зона их действия будет определяться направлением стрелки на табличках, а также расстоянием, указанным на них.
Действие знаков «Стоянка запрещена по нечетным числам месяца» и «Стоянка запрещена по четным числам месяца» может быть обусловлено и применением знака 6.4 «Парковка (парковочное место)» в его сочетании с табличкой 8.2.1. В этом случае знаки прекращают свое действие, и стоянка транспортных средств будет разрешена в любой день.
Указанные знаки не распространяют свое действие на три вида транспортных средств:
- На ТС, управляемые водителями-инвалидами I и II групп или перевозящие таких инвалидов или инвалидов-детей;
- На ТС, принадлежащие федеральной почтовой службе РФ;
- На такси с включенным таксометром.
Важно помнить, что знаки «Стоянка запрещена по нечетным числам месяца» и «Стоянка запрещена по четным числам месяца» «работают» только на той стороне дороги, на которой установлены.
Однако именно здесь возникает принципиально важный момент, связанный с параллельной установкой знаков по обеим сторонам дороги.
Возьмем чисто теоретический пример. В случае одновременного применения знаков «Стоянка запрещена по нечетным числам месяца» и «Стоянка запрещена по четным числам месяца», возникает парадоксальная ситуация.
Так, в 23 часа 59 минут 59 секунд нечетного числа месяца автомобиль, стоящий в зоне действия знака, запрещающего стоянку по четным числам месяца, не нарушает правила. Но ровно через секунду наступает четное число, а вместе с этим автоматически возникает и нарушение правил стоянки. Еще раз отметим, что это — чисто теоретически.
Поэтому законодатель следующим образом определил случай параллельной установки знаков по обеим сторонам дороги: хронологический отрезок с 19 часов и до 21 часа каждых суток определен в качестве времени перестановки ТС. Иными словами, в это время парковка разрешена на любой стороне дороги.
Иными словами, в это время парковка разрешена на любой стороне дороги.
Соответственно и новые сутки начинаются не в 0 часов и 00 минут, а в 21.00 предшествующих суток. Например, 1 июля начинается в 21.00 (30 июня) и продолжается до 19 часов (собственно 1 июля). Затем идет перестановочное время — с 19.00 до 21.00, чтобы с 21.00 (1 июля) началось четное число (то есть 2 июля) и т.д.
Многие курсанты автошкол (да и начинающие водители) мечтают «вбить в голову гвоздь» тому, кто придумал это правило.
Но если копнуть поглубже, то логика законодателя понятна. Конечно, можно, было бы устроить перестановочное время с 23 часов и до 1 часа ночи, но будет ли удобно водителю вылезать из теплой постели, заводить автомобиль и переставлять его на другую сторону дороги, чтобы не нарушить Правила?
Если данная информация была для вас полезна, напишите, пожалуйста, об этом в комментариях. Если возникнут вопросы, пишите, обязательно постараемся вам помочь.
Пдд онлайн от команды autoass!
Содержание статьи:
- знак стоянка запрещена по нечётным
- парковка по четным и нечетным дням
- стоянка по четным и нечетным дням
- парковка по четным и нечетным
Дорожный знак 3.
 29 «Стоянка запрещена по нечетным числам месяца»
29 «Стоянка запрещена по нечетным числам месяца»Принцип действия и правила установки дорожного знака 3.29 «Стоянка запрещена по нечётным числам месяца» совершенно идентичны таковым у знака 3.28 «Стоянка запрещена». Чем же вызвана необходимость установки такого знака? Разве недостаточно установки обычного знака, запрещающего стоянку? Оказывается, нет.
Знак 3.29 обычно устанавливается на узких участках дорог, где может быть затруднён разъезд встречно двигающегося транспорта, а также в местах скопления офисных зданий, различных учреждений, супермаркетов и других мест, которые предполагают парковку автомобильного транспорта. Припаркованные с обеих сторон дороги автомобили могут существенно помешать дорожному движению, тогда как парковка только с одной стороны дороги проблем для трафика не составит. Поэтому этом зачастую знак 3.29 «Стоянка запрещена по нечётным числам месяца» устанавливается на одной стороне дороги, а знак 3.30 «Стоянка запрещена по чётным числам месяца» — на другой.
Правда, подобная установка знаков имеет один интересный нюанс. Что, если автомобиль останавливается на «разрешённой стороне», но водитель оставляет его на ночь? Ведь ровно в 00.00 чётный день сменяется нечётным, и в одну секунду карета превращается в тыквы, а примерный водитель – в нарушителя.
В Правилах дорожного движения этот момент предусмотрен. В случае параллельной установки знаков 3.29 и 3.30 началом следующих суток считается время не в 00.00, а в 21.00, а отрезок времени с 19.00 до 21.00 считается временем перестановки транспортных средств, когда автомобили можно ставить на стоянку с любой стороны. То есть, если водитель не хочет попасть в число нарушителей, он должен позаботиться о том, чтобы в период с 19.00 до 21.00 переставить свой автомобиль на «правильную» сторону.
Знак 3.29 полностью напоминает знак 3.28: синий круг с красной окантовкой, «перечёркнутый» красной полосой, с одним лишь исключением: в его центре имеется вертикальная белая полоска.
Действие знака 3.29 «Стоянка запрещена по нечётным числам месяца» начинается непосредственно в месте его установки, и его запрет действует до следующих участков:
- следующего по ходу движения транспортного средства перекрестка;
- окончания населенного пункта, помеченного соответствующим знаком;
- знака 3.31, обозначающего окончание зоны всех ограничений;
После того, как вышеуказанные участки дороги будут пройдены, стоянка автомобилей автоматически разрешается во все дни месяца.
Знак 3.29 и таблички дополнительной информации
Зона влияния знака 3.29 может быть уточнена при помощи установки табличек и знаков дополнительной информации, а именно:
Так, табличка 8.2.2, установленная вместе со знаком 3.29, указывает то расстояние, на которое распространяется действие знака.
Знак 3.29 может устанавливаться совместно с табличкой 8.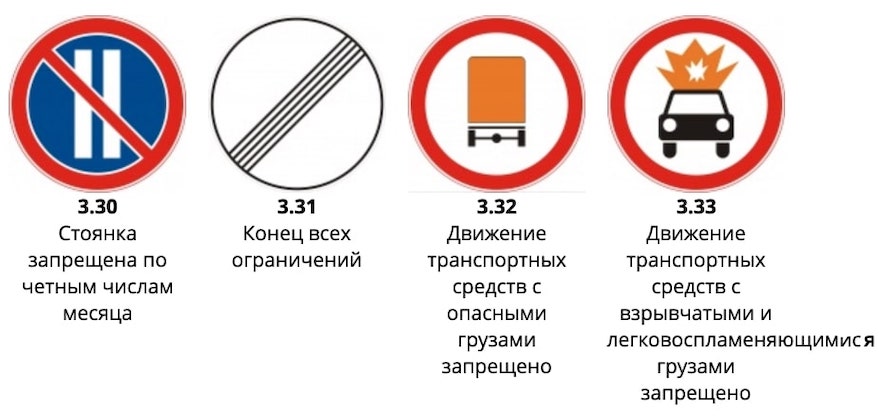 2.3. Эта табличка указывает на окончание зоны действия знака. Проще говоря, стрелка на табличке указывает на то, что знак «Стоянка запрещена по нечётным числам месяца» действует перед местом его установки.
2.3. Эта табличка указывает на окончание зоны действия знака. Проще говоря, стрелка на табличке указывает на то, что знак «Стоянка запрещена по нечётным числам месяца» действует перед местом его установки.
Если на дороге установлена табличка 8.2.4, это говорит водителю о том, что он в данный момент находится в зоне действия знака «Стоянка запрещена по нечётным числам месяца». Эта табличка является дополнительным указанием на действующее ограничение на том участке дороги, где уже действует ранее введенный запрет на стоянку, и режим запрета еще не отменен.
Таблички дополнительной информации 8.2.5 и 8.2.6 (по отдельности или совместно), которые могут быть установлены вместе со знаком «Стоянка запрещена по нечётным числам месяца» используются для того, чтобы обозначить ограничения стоянок возле площадей, зданий и пр. В данном случае стоянка будет запрещена, начиная с места, где установлен знак, в том направлении, в котором указывает стрелка и на том расстоянии, которое указано на знаке.
Зона действия знака 3.29 может быть ограничена при помощи информационного указателя 6.4 «Место для парковки» и таблички 8.2.1, которые, в случае совместной установки указывают на разрешенное для остановки и стоянки место.
Водитель должен помнить, что знак 3.29 «Стоянка запрещена по нечётным числам месяца» действует исключительно с той стороны дороги, с которой он установлен.
Знак 3.29 не распространяется на водителей, имеющих инвалидность первой и второй групп, а также на водителей транспортных средств, которые перевозят таких инвалидов. Такие автомобили обязательно должны быть оборудованы специальными знаками «Инвалид».
Кроме того, знак не действует на такси, у которых включен таксометр, а также на автомобили, принадлежащие российской федеральной почтовой службе.
Читайте также:
– Дорожный знак 3.30 «Стоянка запрещена по четным числам месяца»
– Дорожный знак 3.31 «Конец зоны всех ограничений»
– Дорожный знак 3. 32 «Движение транспортных средств с опасными грузами запрещено»
32 «Движение транспортных средств с опасными грузами запрещено»
Стоянка по четным и нечетным числам месяца в 2021 году
Рассмотрим дорожные знаки запрещающие стоянку по четным и нечетным дням.
«Стоянка» — преднамеренное прекращение движения транспортного средства на время более 5 минут по причинам, не связанным с посадкой или высадкой пассажиров либо загрузкой или разгрузкой транспортного средства.
В отличии от запрещающего знака 3.27 «Остановка запрещена», который запрещает любую остановку, знаки 3.28 «Стоянка запрещена», 3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца» запрещают прекращение движения продолжительностью более 5 минут, которое не связано с посадкой (высадкой) пассажиров или загрузкой (разгрузкой) транспортного средства. То есть, если необходимо остановиться в зоне действия знаков запрещающих стоянку, например для посадки пассажиров и такая остановка займет более пяти минут, то это не будет являться нарушением Правил.
ГОСТ Р 52289-2004. Технические средства организации дорожного движения. Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств.
5.4.25 Знаки 3.28 «Стоянка запрещена», 3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца» применяют для запрещения стоянки.
3.28 «Стоянка запрещена». Запрещается стоянка транспортных средств.
3.29 «Стоянка запрещена по нечетным числам месяца».
3.30 «Стоянка запрещена по четным числам месяца».
Основные требования установки и применения знаков запрещающих стоянку, такие же как и для запрещающего знака 3.27 «Остановка запрещена», с ними можно ознакомиться по ссылке: Знак 3.27 «Остановка запрещена» и зона его действия.
Мы остановимся на ситуации, когда на проезжей части дороги, на ее противоположных сторонах установлены одновременно знаки 3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца». Одновременное применение знаков 3.29 и 3.30 на проезжей части дороги, необходимо для возможности уборки улиц коммунальными службами.
Одновременное применение знаков 3.29 и 3.30 на проезжей части дороги, необходимо для возможности уборки улиц коммунальными службами.
При таком применении знаков, стоянка запрещена по четным и нечетным дням на соответствующей стороне проезжей части дороги.
На снимке, знаки 3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца» установлены на противоположных сторонах. Автомобили поставлены на стоянку также на обеих сторонах проезжей части дороги. В зависимости от числа месяца (четное или нечетное), на одной из сторон дороги, автомобили будут припаркованы с нарушением Правил.Согласно Правилам, при одновременном применении знаков 3.29 и 3.30 на противоположных сторонах дороги, в период времени с 19 часов до 21 часа, разрешается поставить транспортное средство на стоянку на любой стороне проезжей части.
При одновременном применении знаков 3.29 и 3.30 на противоположных сторонах проезжей части разрешается стоянка на обеих сторонах проезжей части с 19 часов до 21 часа (время перестановки).
Это сделано для того, чтобы владельцы транспортных средств в конце дня могли спокойно переставить свои автомобили на соответствующую сторону проезжей части дороги в соответствии с наступающими сутками. Соответственно, следующие сутки для стоянки, в соответствии с Правилами при одновременном применении знаков 3.29 и 3.30, наступают в 21 час.
Рассмотрим на примере (изображение ниже).
Сегодня 1 число месяца (нечетное число), следовательно поставить автомобиль на стоянку разрешено на правой стороне проезжей части. Если планируем оставить транспортное средство для стоянки и на следующие сутки (четное число), то в соответствии с Правилами после 21 часа, автомобиль должен быть припаркован уже на противоположной стороне (на левой стороне) проезжей части. Перестановку транспортного средства необходимо выполнить с 19 часов до 21 часа.Почему время перестановки именно такое, это сделано для удобства владельцев транспортных средств, чтобы в конце рабочего или выходного дня можно было спокойно поставить автомобиль на стоянку и не делать это в 00 часов 00 минут, когда наступят следующие календарные сутки.
Если у Вас остались вопросы пишите в комментариях или в группе ВКонтакте — ШКОЛА-ПДД, попробуем вместе разобраться. Всем безопасной дороги и правильной стоянки!
Опубликовано 08 октября 2019 года, обновлено 08 сентября 2020 года.
Знаки парковки по четным и нечетным числам месяца в 2020 году
Для чего необходим знак, запрещающий парковку по определенным дням месяца. Как правильно определить разрешенное время и протяженность стоянки. Исключения из общего правила.
Дорожные знаки — один из способов регулирования движения на городских улицах и загородных дорогах. Однако некоторые из них порой оказываются не совсем понятны водителям.
Например, знаки запрета парковки по четным и нечетным числам вызывают вопрос, с чем связана такая избирательность? Дадим на него развернутый ответ.
Основные моменты
О том, что стоянка транспортных средств в данном месте запрещена, водителей предупреждает сплошная линия разметки вдоль карая проезжей части и специальные запрещающие знаки:
- стоянка запрещена;
- стоянка запрещена по нечетным числам;
- стоянка запрещена по четным числам.

Знак «Стоянка запрещена» представляет собой синий круг с красным окаймлением, наискось перечеркнутый красной же полосой.
В зоне действия такого знака запрещена только стоянка, но не остановка. Знаки, запрещающие стоянку по определенным дням, дополнены вертикальными белыми полосами.
Одна такая полоса означает запрет на стоянку по нечетным числам месяца, а две полосы запрещают стоянку по четным датам.
Знаки могут применяться как самостоятельно, так и в сочетании с информационными табличками, сообщающим водителям дополнительные сведения:
- о принудительной эвакуации неправильно припаркованных машин;
- о протяженности зоны действия знака, если она отличается от обычной;
- об окончании действия запрета.
Необходимые термины
Запрет на стоянку по нечетным дням означает, что на данной стороне улицы нельзя парковать машину по нечетным числам любого месяца — 1, 3, 5,….
29, 31.
И напротив, можно оставить 2, 4 и т. д. Останавливаться на данной стороне можно в любой день.
Стоянка по четным дням запрещена означает, что в зоне действия знака нельзя припарковаться в любую четную дату месяца — 2, 4,6 … 28, 30.
Во все остальные дни стоянка под данным знаком будет вполне законной. Остановка разрешена всегда.
Время перестановки — ежедневный период, длящийся с 19:00 до 21:00, когда парковка разрешена на любой стороне улицы.
Но такое понятие применяется только на тех улицах, где оба знака, запрещающих парковку в определенные дни, установлены одновременно.
Начало нечетных и четных дат приходится на 21:00. То есть действие знака «Парковка запрещена по четным дням» начинается в 21:00 1, 3, 5 и т. д. числа каждого месяца.
С нечетными датами все обстоит ровно наоборот — они начинаются в 21:00 2, 4, 6 и пр. числе месяца.
Что они означают
Знаки 3.29 и 3.30 запрещают водителям оставлять свои автомобили в зоне их действия в определенные даты.
Фото: дорожный знак 3.29 — 3.30
Под стоянкой в данном случае понимается прекращение движения транспортного средства более чем на 5 минут.
Двигатель при этом может быть включен, а водитель находиться внутри. Исключение делается лишь для машин почты, такси и инвалидов.
Помимо временного критерия стоянку определяет и отсутствие действий, связанных с погрузкой или выгрузкой различных предметов, а также посадку или высадку пассажиров.
Останавливаться для того, чтобы выполнить такие манипуляции указанные знаки не запрещают. Не будет нарушением и вынужденная стоянка, вызванная неисправностью автомобиля.
Но водитель должен выставить знак аварийной остановки и включить световую сигнализацию «аварийку».
Какими нормативными актами регулируется
Знаки 3.29 и 3.30 приведены в Приложении 1 Правил дорожного движения в разделе «Запрещающие знаки».
ПДД регулируются и основные моменты применения таких знаков:
| Распространение действия | Только на ту сторону улицы, где знак находится |
| Протяженность действия такого знака до перекрестка | Границы населенного пункта или отменяющего знака |
| Время перестановки | При совместном применении знаков |
| Исключение | Для почтовых и инвалидных автомобилей, легальных такси |
Ответственность за несоблюдение запрета, установленного таким знаком предусмотрена Кодексом об административных нарушениях.
В статье 12.16 КоАП за такое нарушение установлен штраф в 1500 р. Если же предписания знака проигнорированы в Москве или Санкт-Петербурге, то размер штрафа увеличивается вдвое и составит уже 3000 р.
Автомобиль, припаркованный вопреки правилам, может быть принудительно эвакуирован на основании ст. 27.13 КоАП.
Особенности данных знаков
Главная особенность знаков 3.29 и 3.30, запрещающих стоянку в определенные дни месяца, заключается в том, что их действие распространяется только на одну сторону улицы.
На противоположной стороне стоянка разрешена в любое время, если только там не установлен аналогичный знак. Допускается одновременная установка обоих знаков, но на разных сторонах улицы.
Запрет на парковку автомобилей по четным или нечетным дням не распространяется на простую остановку, с целью посадить или высадить пассажиров. Такая остановка возможна в любой день, на любой из сторон улицы, нарушением это не будет.
Для чего нужна парковка по разным дням
Дорожные знаки, запрещающие парковку по определенным дням, имеют определенную логику размещения.
Они применяются на относительно узких улицах, где наблюдается большое скопление припаркованных автомобилей.
Причиной такой их плотности могут быть расположенные поблизости многочисленные офисы, популярные кафе или зоны отдыха.
Одновременное занятие края проезжей части с обеих сторон такой улицы, существенно ее сужает. В результате водителям становится трудно разминуться, возникают заторы.
При любом чрезвычайном происшествии спецтехника не сможет быстро добраться по забитой машинами улице к нужному месту.
Для регулирования движения в таких «узких местах» и используются знаки 3.29 и 3.30. Если все автомобили припаркованы только на одной стороне улицы, остается достаточно места для встречного разъезда, маневрирования машин экстренных служб.
Кроме того, одна сторона улицы оказывается также доступна для очистки от снега в зимний период, от пыли песка — в летний.
Как вычислить зону распространения таблички
Чтобы не ошибиться с протяженностью зоны действия знаков, запрещающих парковку в те или иные дни, необходимо руководствоваться общими положениями ПДД.
Если такой знак установлен один, без поясняющих табличек или совместно со знаком «Работает эвакуатор», то запрет распространяется на соответствующую сторону улицы вплоть до:
- ближайшего после знака перекрестка;
- такого же знака, но уже с табличкой 8.2.3;
- границы населенного пункта;
- знака «Отмена всех ограничений».
Если запрещающий знак имеет поясняющие таблички, то для определения протяженности зоны, запретной для стоянки, необходимо пользоваться информацией именно с них.
Как правило, применяется табличка 8.2.2, показывающая протяженность зоны запрета в метрах.
Фото: дорожный знак 8.2.2
Иногда запрещение стоянки ограничивается определенными временными рамками, о чем информирует соответствующая табличка, например, в деловом центре это могут быть дневные часы, а в жилых районах, напротив, вечерние и ночные.
Видео: знаки 3.29-3.30
Время действия стоянки по четным и нечетным дням
Временем начала новых суток принято считать полночь — 0:00. Однако в Правилах дорожного движения принят иной вариант — новые сутки отсчитываются с наступления темного времени — с 21:00.
Это перекликается с традицией, действующей во многих странах Европы. В применении такого правила есть свой резон — водители имеют возможность вечером, возвращаясь с работы или отдыха, сразу поставить машину на «правильной» стороне и не выходить перемещать ее в полночь.
Для удобства водителей, работающих или проживающих в зоне действия сразу двух знаков по обеим сторонам улицы, действует дополнительный период, когда стоянка разрешена одновременно везде.
Это промежуток с 19:00 до 21:00 ежедневно. Он предназначен для того, чтобы без спешки переставить автомобиль на сторону, где с нового дня парковка разрешается или сразу занять там место на следующие сутки.
Эти два часа так и называются — время перестановки.
Есть ли исключения из правил
Несмотря на то, что действуют знаки парковки по четным и нечетным числам в ПДД на всех участников движения, из общего правила есть ряд исключений.
Не будут являться нарушителями водители, припарковавшие в зоне действия такого знака автомобили:
| Почтовой службы | Если на бортах имеется соответствующее цветографическое изображение |
| Легкового такси | С необходимыми обозначениями и включенным таксометром |
| Управляемые инвалидами 1 или 2 группы | Или перевозящие людей с ограниченными возможностями |
Еще одним исключением будет парковка в так называемое «время перестановки». Согласно ПДД оно длиться с 19:00 до 21:00 одного и того же дня.
В этот период разрешается стоянка автомобилей на обеих сторонах тех улицах, где одновременно применяются оба знака.
После 21:00 начинается отсчет новых суток и парковка на «неположенной» стороне становится наказуемой. Если же знак на улице установлен только один, то время перестановки на ней не действует.
Знак запрета парковки по четным или по нечетным дням применяется для регулирования движения на узких улицах.
Нарушение предписаний такого знака является правонарушением, наряду с другими примерами неправильной парковки. На водителя накладывается штраф, а автомобиль может быть эвакуирован.
Зачем на самом деле нужны знаки, запрещающие парковку по четным и нечетным дням — ГАИ
Как оказалось, многие водители — и даже те, кто за рулем далеко не первый год — задаются вопросом, с какой целью дорожники устанавливают знаки, запрещающие парковку с той или иной стороны улицы в зависимости от даты. Официальная версия гласит, что они нужны для удобства уборки дорог. Как же обстоят дела на самом деле, выяснил портал «АвтоВзгляд».
Вообще знаки-близнецы 3. 29 и 3.30 вводились с целью разгрузить улицы, чтобы коммунальные службы могли спокойно выполнять свои обязанности: в зимнее время очищать дороги от снега, а в летнее — от пыли, листьев и прочего природного «мусора». Кроме того, подразумевалось, что это нехитрое решение хоть мало-мальски способствует снижению трафика.
29 и 3.30 вводились с целью разгрузить улицы, чтобы коммунальные службы могли спокойно выполнять свои обязанности: в зимнее время очищать дороги от снега, а в летнее — от пыли, листьев и прочего природного «мусора». Кроме того, подразумевалось, что это нехитрое решение хоть мало-мальски способствует снижению трафика.
Задумка с разбитой по дням стоянкой — заимствованная, кстати, за рубежом — быть может, сама по себе и не плоха, да вот только реализована она у нас как-то невнятно. Коммунальщики по-прежнему наводят порядок на улицах сразу с двух сторон — припаркованные авто им ничуть не мешают. В то время как водители, утомленные бессмысленными нововведениями, оплачивают солидные штрафы, путаясь в требованиях знаков.
И не значит ли это, что истинный смысл односторонних парковок в чем-то другом?
Фото: Московский Комсомолец
Тем, кто знаком с Правилами дорожного движения постольку-поскольку, напомним, что знаки 3.29 и 3.30 действуют строго по своему календарю, немного опережающему реальное время. Так, если таблички установлены с двух сторон улицы, то их предписания надобно соблюдать до семи часов вечера. В течение следующих двух часов можно свободно парковаться по оба края проезжей части, а в 21.00 на таких дорогах уже наступает следующий день.
Так, если таблички установлены с двух сторон улицы, то их предписания надобно соблюдать до семи часов вечера. В течение следующих двух часов можно свободно парковаться по оба края проезжей части, а в 21.00 на таких дорогах уже наступает следующий день.
Учитывая, сколько на российских дорогах водителей, твердо знающих лишь про «кирпич» и сигналы светофора, ничуть не удивительно, что масса автомобилистов попадает в ловушку знаков-близнецов. Если «прогуляться» по тематическим интернет-форумам, можно найти множество сообщений от пользователей, жалующихся на «безосновательную» эвакуацию с «правильной» стороны дороги в период с 21.00 до 00.00.
Фото: Московский Комсомолец
Это наводит на мысль, что коварные «зеленые крокодилы» отнюдь не случайно «пасутся» поздними вечерами на улицах, украшенных знаками 3.29 и 3.30. Да и таблички там эти висят вовсе не для того, чтобы помогать коммунальщикам. Истинный смысл задумки — содрать с моторизованных граждан побольше денег. Впрочем, и это не удивительно.
К слову сказать, в СМИ уже неоднакратно поднимался вопрос целесообразности установок на столичных улицах знаков 3.29 и 3.30. С тем, что в этом решении нет никакого смысла, давно уже согласились и в Центре огранизации дорожного движения (ЦОДД). В пределах Садового кольца таблички не сыскать — убрали. Что же до спальных районов Москвы, то там, очевидно, они будут висеть еще долго. А почему — мы уже выяснили.
122623
122623
15 февраля 2019
37339
Знак 3.29 — Стоянка запрещена по нечетным числам месяца
08.12.2018
При одновременном применении знаков 3.29 и 3.30 на противоположных сторонах проезжей части разрешается стоянка на обеих сторонах проезжей части с 19 часов до 21 часа (время перестановки).
Зона действия знака может быть уменьшена установкой в конце зоны его действия повторного знака 3.29 с табличкой 8.2.3 или применением таблички 8.2.2
Одна сторона дороги НЕ на инвалидов НЕ на такси До ближайшего перекрестка (до конца населенного пункта) НЕ на почту
Разрешено ли Вам произвести остановку для посадки пассажира?
| 1. | Не разрешено. | |
| 2. | Разрешено только по нечетным числам месяца. | |
| 3. | Разрешено только по четным числам месяца. | |
| 4. | Разрешено. |
Знак «Стоянка запрещена по нечетным числам месяца» запрещает только стоянку. Следовательно, остановиться в этом месте, в том числе и для посадки пассажиров, Вы можете в любой день месяца.
Разрешено ли Вам поставить автомобиль на стоянку в указанном месте по нечетным числам месяца?
| 1. | Разрешено. | |
| 2. | Разрешено только после 19 часов. | |
| 3. | Запрещено. |
Ответ
- Зона действия знака «Стоянка запрещена по нечетным числам месяца» распространяется до ближайшего перекрестка, поэтому в указанном месте стоянка вашего ТС по нечетным числам месяца запрещена.
- Однако при одновременной установке знаков «Стоянка запрещена по нечетным числам месяца» и «Стоянка запрещена по четным числам месяца» эти знаки действуют только до 19 часов. Следовательно, Вы можете поставить автомобиль на стоянку после 19 часов.
© 2016-2021 [email protected]
Знак 3.30 Стоянка запрещена по четным числам месяца
06.02.2016
Знак 3.30 «Стоянка запрещена по четным числам месяца» применяют для запрещения стоянки.
Знак 3.30 устанавливают на той стороне дороги, на которой вводится запрещение.
При одновременном применении знаков 3.29, 3.30 на противоположных сторонах проезжей части с 19 до 21 ч (время перестановки) разрешается стоянка на обеих сторонах проезжей части.
Для запрещения остановки или стоянки вдоль одной из сторон площади, фасада здания и т.п. знак 3.30 с одной из табличек 8.2.5, 8.2.6 или с обеими табличками одновременно допускается устанавливать напротив въезда на площадь, подъезда к зданию и т.п. лицевой стороной к водителям транспортных средств.
В населенных пунктах повторный знак 3.30 диаметром 250 мм (без табличек 8.2.2 — 8.2.4) для подтверждения введенных ранее ограничений допускается устанавливать за выездами с прилегающих территорий, признаки которых могут неоднозначно распознаваться водителями транспортных средств.
Действие знака 3.30 не распространяется на транспортные средства, управляемые инвалидами I и II групп или перевозящие таких инвалидов, если на этих транспортных средствах установлен опознавательный знак «Инвалид».
В зоне действия знака 3.30 допускается стоянка автомобилей организаций федеральной почтовой связи, имеющих на боковой поверхности кузова белую диагональную полосу на синем фоне, а также стоянка такси с включенным таксометром.
Действие знака распространяется от места установки знака до ближайшего перекрестка за знаком, а в населенном пункте при отсутствии перекрестка — до конца населенного пункта.
Указанный знак должны быть повторно установлены после окончания населенного пункта или непосредственно за перекрестком при необходимости сохранить ограничения, введенные знаком, установленным соответственно до перекрестка или конца населенного пункта.
Зона действия знака 3.30 может быть уменьшена установкой в конце зоны их действия повторных знаков 3.30 с табличкой 8.2.3 (что является предпочтительным) или применением таблички 8.2.2 либо установкой другого знака из указанного перечня или установкой знака 6.4 «Место стоянки» с табличкой 8.2.1 «Зона действия».
Действие знака 3.30 распространяется на сторону дороги, где установлен знак.
Дорожные знаки по ГОСТу
ПДД – Остановка и стоянка
Штраф за нарушение правил остановки или стоянки
Эвакуация автомобиля в вопросах и ответах
Знак 3.31 «Конец зоны всех ограничений»
Нечетных и четных чисел
Что такое четные и нечетные числа?
Целое число, которое можно разделить на 2, является четным числом, а целое число, которое нельзя разделить на 2, является нечетным числом. Они могут быть как положительными, так и отрицательными. Нечетные числа всегда находятся между четными и наоборот.
Чтобы различать четные и нечетные числа, всегда ищите их конечную цифру. Последняя цифра четного числа всегда равна 0, 2, 4, 6 или 8, а последняя цифра нечетного числа всегда равна 1, 3, 5, 7 или 9.
Примеры
Несколько примеров четных чисел:
-22, -10, 0, 6, 18, 234.
Вышеупомянутые числа четные, потому что они заканчиваются на 0, 2, 4, 6 или 8.
Несколько Примеры нечетных чисел:
-101, -17, 1, 9, 23, 985.
Приведенные выше числа нечетные, потому что они заканчиваются на 1, 3, 5, 7 или 9.
Свойства
нечетные и четные числа обладают особыми свойствами в отношении алгебраических операций (сложение, вычитание и умножение).Когда мы применяем алгебраические операции к двум четным или нечетным числам, мы всегда получаем четное или нечетное число. Мы исключаем деление здесь, потому что деление иногда дает результат в дробях, когда речь идет об особых свойствах.
- Когда мы складываем или вычитаем два четных числа, результатом всегда будет четное число. Например, 6 + 4 = 10
6 — 4 = 2
- Когда мы складываем или вычитаем четное и нечетное число, результат всегда нечетный. Например, 7 + 4 = 11
7 — 4 = 3
- Когда мы складываем или вычитаем два нечетных числа, результатом всегда будет четное число. Например, 7 + 3 = 10
7 — 3 = 4
- Когда мы умножаем два четных числа, результатом всегда будет четное число. Например,
6 × 4 = 24 - Когда мы умножаем четное и нечетное число, результатом всегда будет четное число. Например,
7 × 4 = 28 - Когда мы умножаем два нечетных числа, результатом всегда будет нечетное число. Например,
7 × 3 = 21
Обобщение нечетных и четных чисел
Мы также можем обобщить четные и нечетные числа.Например, если «n» — четное число, то следующее нечетное число будет «n + 1», а следующее четное число — «n + 2» и так далее. Аналогично, если «n» — нечетное число, то следующее четное число — «n + 1», следующее нечетное число — «n + 2» и так далее.
Например, если мы хотим записать серию из пяти нечетных чисел, начиная с 73, мы можем записать это как:
73, 73 + 2, 73 + 4, 73 + 6, 73 + 7
73, 75 , 77, 79, 81
Таблица чисел
Следующая таблица представляет собой таблицу чисел от 1 до 100, где нечетные числа выделены желтым цветом , а четные числа выделены зеленым цветом .
Предыдущий урок | Главная страница | Следующий урокЭвены и шансы | Математические решения
Урок для детского сада, первый и второй класс
Стефани Шеффилд
Многие первоклассники научились считать по два, минимум до десяти.Некоторые выучили пение «Два, четыре, шесть, восемь, кого мы ценим». И некоторые знают, что когда вещи одинаковы, мы часто говорим, что они равны. Однако большинство первоклассников не задумывались о связи этих представлений со свойствами четных чисел или о разнице между четными и нечетными числами. Урок Стефани Шеффилд помогает развить у детей представление о том, что количество есть даже если его можно разделить на половинки, а также помогает им увидеть закономерность, согласно которой четные числа заканчиваются на 0, 2, 4, 6 или 8, а нечетные числа заканчиваются на 1, 3, 5, 7 или 9.Этот урок будет включен в готовящуюся к выпуску книгу Стефани Teaching Arithmetic: Lessons for First Grade , , которая будет опубликована Math Solutions Publications осенью 2001 года.
Каждый год наша школа PTA проводит общешкольный сбор средств. Однажды, чтобы заинтересовать детей этим событием, мы провели собрание, чтобы объявить о распродаже. Мамы PTA предоставили приз за каждое занятие, которое было упаковано как подарок. Если хотя бы половина учеников в классе продаст хотя бы один предмет, класс сможет открыть коробку и забрать приз.
Когда мы вернулись в класс после собрания, я поставил коробку на картотечный шкаф. Я спросил класс: «Если половина детей в нашем классе должна продать один предмет, сколько детей нужно для этого?»
Руки взметнулись в воздух, и цифры разлетелись по кругу, но было ясно, что существуют разногласия по поводу того, сколько учеников составляет половину класса. Я решила использовать кубики с кнопками, чтобы помочь детям найти ответ.
Я снял с полки контейнеры с кубиками и поставил по одной на каждый стол.Я сказал: «Каждому из вас нужно девятнадцать кубиков. Кто знает, зачем вам девятнадцать кубиков? »
Кристин предварительно ответила: «Потому что нас девятнадцать?» «Что будет представлять каждый куб?» Я спросил.
«Один ребенок», — ответила Кристин.
Затем я дал указания классу. «Построй поезд из своих девятнадцати кубиков. Посоветуйтесь с другом, чтобы убедиться, что ваши поезда такого же размера ». Я подождала, пока это сделают все дети.
Тогда я сказал: «А теперь сломайте свой поезд пополам.«Когда дети разделили свои поезда на две части, некоторые подумали, что у них два одинаковых поезда. Их новые поезда выглядели такими же, и они не думали проверять, ставя их или кладя на стол. Алекс, однако, поднял свои две фигуры.
«Не думаю, что это правильно. Они не совпадают », — сказал он.
«Да, они должны быть одинаковыми», — согласилась Андреа, сравнивая два своих поезда. «Что ты имеешь в виду?» Я спросил.
«Это как яблоко», — объяснил Ричард.«Если вы разрежете его пополам, вы и ваш друг получите по частям. Но это должно быть справедливо ».
«Итак, если разрезать что-то пополам, сколько частей вы получите?» Я спросил. «Два!» они все вместе сказали.
«А что вы можете сказать мне о двух частях?» Я продолжил. «Они всегда такие же», — ответил Мукунд.
«Равные», — добавил Кристиан.
«Вопрос в том, сколько учеников в половине нашего класса?» Я сказал. «Как кубики могут помочь вам узнать?»
Кевин ответил: «Либо восемь, либо девять.В одном из поездов их восемь, а в другом — девять ». Кевин неправильно подсчитал кубики, но он знал, что поезда находятся на расстоянии одного куба друг от друга.
Я сказал: «Но если мы разделим наш поезд на половинки, все они должны быть одинаковой длины. Как можно разделить поезд из девятнадцати кубиков пополам? » Студенты пробовали снова и снова, соединяя кубики вместе, а затем разделяя их. Каждый раз результат был неравным.
Наконец, Хлоя сказала: «Я просто не думаю, что это сработает. Один поезд всегда на куб выше.”
«Это сработает, если мы выбросим один куб», — предположил Кристиан.
«Не пойдет!» — раздраженно воскликнула Кирра. «Один из поездов всегда больше другого».
Поскольку некоторые из студентов были разочарованы, я остановил их расследование на несколько минут обсуждения. Я сказал: «Это сложно потому, что мы не можем разрезать куб пополам и положить часть его в один поезд, а часть — в другой. Но использование кубиков по-прежнему является хорошей моделью для решения нашей проблемы о том, сколько детей составляет половину класса, потому что мы также не можем разделить ученика на части.Лучшее, что мы можем сделать для этой задачи, — это сказать, что половина нашего класса — это либо девять, либо десять ».
«Давай используем девять!» — воскликнула Андреа. «Так у нас будет больше шансов открыть коробку!»
Затем я расширил вопрос, чтобы студенты использовали кубики для деления других целых чисел пополам. Я сказал: «Кирра сказала, что девятнадцать не работают. Кто знает, что она имеет в виду? »
Лорен сказала: «Она имеет в виду, что вы не можете разделить его на две равные части».
«Знаете ли вы, сколько кубиков может иметь поезд, чтобы его можно было разделить пополам?» Я спросил.
Хлоя подняла руку. «Если бы мы избавились от куба, у нас было бы восемнадцать, и это работает», — сказала она. Дети убедились с помощью кубиков, что это так. Я подошел к доске и провел вертикальную линию, чтобы получилось два столбца. Я назвал левый столбец «Работает», а другой столбец «Не работает». Я записал 19 в разделе «Не работает» и 18 в разделе «Работает».
Я привлек внимание детей и дал указания для дальнейших исследований. «Каждый из вас выберет число от десяти до двадцати.Тут же руки нырнули в емкости с кубиками. Я потратил минуту, чтобы привлечь их внимание, и подождал, пока все руки не уберутся с кубиков.
Затем я продолжил: «После того, как вы отсчитаете кубики, сделайте поезд и попробуйте разбить его пополам. Будьте готовы сообщить классу выбранный вами номер и его принадлежность к столбцу «Работает» или «Не работает».
Дети пошли работать. Некоторые отстегивали кубики в своих поездах, а затем снова начинали отсчитывать кубики. Некоторые начали с поезда из девятнадцати человек и забрали несколько кубиков.
Когда я увидел, что все дети изучили хотя бы одно число, я обратил их внимание. Я попросил нескольких детей сообщить о числах, которые они исследовали, записав каждое число на доске в нужном столбце, чтобы указать, можно ли его разбить на две равные части.
После того, как я записал шесть чисел, я сосредоточил внимание класса на метках столбцов. Я спросил: «Кто может объяснить, что мы подразумеваем под« работает »и« не работает »?
Я подождал, пока большинство детей не поднимут руки, и затем позвал Мукунда.«Все числа, которые работают, вы можете сделать два поезда, которые совпадают с ними», — сказал он.
Далее я позвонил Татьяне. «Эти числа, — сказала она, указывая на столбец« Не работает », — у всех есть остатки, когда вы пытаетесь разбить его пополам, но другие работают без остатка».
Я продолжал просить детей сообщать числа, пока я не записал все числа от 10 до 20. Иногда дети сообщали числа, которые я уже записал. В этих случаях мы использовали информацию в качестве проверки.
Затем я попросил класс рассмотреть числа меньше десяти, на этот раз сначала сделав прогноз о том, подойдет ли это число, а затем построил поезд и разделил его на две части. Для начала я спросил класс: «Как вы думаете, шесть подойдут или нет?»
Ричард ответил: «Думаю, так и будет, потому что я знаю, что три и три — шесть». Некоторые дети согласились, а другие не были уверены.
Я сказал: «Когда вы делаете предсказание, как это сделал Ричард, вы можете проверить свое предсказание с помощью кубиков.Вы бы построили поезд из шести кубиков и посмотрели, сможете ли вы его разбить пополам ».
Я немедленно запретил детям это делать и дал классу еще одно направление. Я сказал: «Посмотрите, что вы можете узнать о числах меньше десяти. Каждый раз делайте сначала прогноз, а затем проверяйте свою идею с помощью кубиков ». Дети снова занялись делом.
«Все дублёры работают!» — воскликнула Андреа через несколько минут. «Три и три — шесть, четыре и четыре — восемь, а пять и пять — десять!»
Лорен остановилась и посмотрела на схему.Затем она посмотрела на Андреа и сказала: «Все числа в графе« Работы »- двойные. Видите, там восемь и восемь — шестнадцать, а шесть и шесть — двенадцать ».
Еще через несколько минут я снова привлек внимание класса. Я попросил студентов сообщить цифры, которые они исследовали, и я записал их в нужные столбцы. Я быстро проверил, что записал все числа.
Затем я сказал: «Есть еще один ярлык, который мы можем присвоить каждой из этих колонок». На доске я написал четное число, выше «Работает» и нечетное число выше «Не работает.”
«У нас в классе четное или нечетное количество учеников?» Я спросил.
«Нечетное число!» был громкий ответ.
«Может ли кто-нибудь объяснить, что, по вашему мнению, такое четные числа?» Я спросил.
Джесси вызвался: «Все четные числа, из них можно составить поезд, а затем два четных, но нечетные числа не работают». Головы кивали, и дети шептали в знак согласия.
Теперь я задал связанный с этим вопрос. «Что, если бы у нас было девятнадцать печенек? Можно ли разделить их на две равные части? Поговорите со своим соседом о том, что вы думаете.”
Через несколько минут я попросил обсуждения. Кьерра подняла руку. «Файлы cookie — это разные вещи», — сказала она. «Печенье можно разрезать пополам, но нельзя — кубиками».
Изменение порядка и запись
Я попросил каждого ученика взять лист бумаги и карандаш, нарисовать линию и обозначить левый столбец «Четные числа» и правый столбец « нечетные числа». Я сделал это на доске и подождал, пока они все это сделают в своих бумагах.Одна из причин, по которой я хотел, чтобы у них был опыт записи самих чисел, заключается в том, что иногда, когда они пишут сами, они замечают закономерности, которые они пропустили, глядя на доску. Кроме того, это служит моделью для организации списков чисел и дает им модель для правильного формирования чисел. И, наконец, если они заберут эту пластинку домой, это может вызвать разговор с их родителями о математике, которую они делали сегодня в школе. Бумаги в руках служат отправной точкой для этого обсуждения и помогают им вспомнить математику.
«Каждый из вас запишет числа из каждого столбца, но мы расположим числа в порядке от наименьшего к наибольшему. Давай сделаем это вместе. Какое наименьшее число вы видите на доске в столбце «Четные числа»? » Все они ответили: «Два», и я написал это в верхней части новой колонки, которую я пометил. Следующим по величине числом, которое они нашли, было четыре, затем шесть, затем восемь. К настоящему времени многие из детей заметили, как работает счет по два, и рассказали быстро, без поиска. Но поскольку многие из них менее уверенно считали на два больше, чем десять или двенадцать, они немного сбавили скорость.Таким же образом мы разместили номера в столбце «Нечетные».
Когда мы заказали все числа, я спросил: «Какие закономерности вы замечаете, когда пишете числа таким образом?»
Ричард поднял руку. «Четные числа идут два, четыре, шесть, восемь, затем числа справа идут ноль, два, четыре, шесть, восемь».
«И нечетные числа идут один, три, пять, семь, девять», — сказал Анджело.
Математика, лежащая в основе четных и нечетных чисел, и их связь с двойными и половинными числами важны для растущего чувства числа первоклассников.Хотя это расследование возникло в результате естественной ситуации в нашем классе, такая возможность не всегда появляется. Тем не менее, я могу предоставить детям такую же возможность, построив урок вокруг другой ситуации, которая требует выяснить, сколько детей в половине класса. Например, если мы разделим класс на две команды, сможем ли мы иметь одинаковое количество детей в каждой команде? Или, если половина нашего класса сделает фотографии до обеда, а половина — после обеда, сколько будет в каждой группе? Независимо от проблемы, я всегда использую кубики, чтобы у детей была возможность проверить свое мышление с помощью физических объектов.
Из выпуска Интернет-бюллетеня № 1, лето 2001 г.
Что такое четные и нечетные числа?
Четные и нечетные числа
Число, которое делится на 2 и дает остаток от 0, называется четным числом. Нечетное число — это число, которое не делится на 2. Остаток в случае нечетного числа всегда равен «1».
Свойство, по которому мы классифицируем целое число в математике как четное или нечетное, также известно как четность.
Идентификационное четное или нечетное число1. Понимая число на месте «единиц»
В этом подходе мы анализируем число в разряде «единиц» целого числа, чтобы проверить, является ли число четным или нечетным.
Все числа, заканчивающиеся на 1,3,5,7 и 9, являются нечетными. Например, такие числа, как 11, 23, 35, 47 и т. Д., Являются нечетными числами.
Все числа, оканчивающиеся на 0,2,4,6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами.
| 25, 32, 38, 87, 95, 64, 76, 53 | |
| Четный | Нечетный |
| 32, 38, 64, 76 | 25, 87, 95, 53 |
2. По группировке
Если мы разделим число на две группы с равным количеством элементов в каждой, то это будет четное число. В случае нечетных чисел при группировке мы получаем остаток 1.
- Группами по два в каждой
Для числа, если оно образует несколько групп по два без остатка, это четное число. В случае остатка число является нечетным числом.
Данная таблица объясняет результат, когда мы применяем разные операции к набору двух чисел.
Заявка
Элементарные навыки распознавания чисел полезны в старших классах для изучения математики, естественных наук и систем коммуникации.Мы применяем эту концепцию при проектировании схем с использованием логических вентилей и двоичных кодов. В древней математике изучение геометрических фигур началось с разделения фигур на четные и нечетные по количеству сторон.
Интересные факты
|
Четные и нечетные числа | Блестящая вики по математике и науке
Четное число имеет четность 000, потому что остаток при делении на 222 равен 000, а нечетное число имеет четность 111, потому что остаток при делении на 222 равен 111.Например, 0,2,4,10, −60,2,4,10, -60,2,4,10, −6 — все четные числа, потому что они оставляют остаток 0 при делении на 222. Целые числа 1 , 3,5,11, −71,3,5,11, -71,3,5,11, −7 — все нечетные числа, потому что они оставляют остаток 1 при делении на 222.
Каждое целое число может быть четным или нечетным, и ни одно целое число не может быть четным или нечетным. Это включает 0, что является четным.
Выясните, является ли 1729 четным или нечетным числом.
Поскольку остаток, полученный при делении 1729 на 2, равен 1, 1729 является нечетным числом.
ИЛИ \ text {ИЛИ} ИЛИ
Число 1729 оканчивается цифрой «9». Таким образом, это нечетное число. □ _ \ квадрат □
Выясните, является ли 1000 четным или нечетным числом.
Поскольку остаток, полученный при делении 1000 на 2, равен 0, 1000 — четное число.
ИЛИ \ text {ИЛИ} ИЛИ
Число 1000 заканчивается цифрой «0». Таким образом, это четное число. □ _ \ квадрат □
а) (б) (c) Ни один из вышеперечисленных
Какое из утверждений относительно числа −163? -163? −163 верно?
(а) Это нечетное число.
(b) Это четное число.
(c) Это не четное и нечетное число.
Отправьте свой ответ
Сколько из следующих 10 чисел являются четными целыми числами?
0,1, −2,3, −1,5.0, −2,4,2 × 2, −2 × 3,5,22 \ begin {array} {rrrrr} 0, && 1, && — 2, && 3, && — 1, \\ 5.0, && — 2.4, && 2 \ times 2 , && — 2 \ times 3.5, && \ frac {2} {2} \ end {array} 0,5.0, 1, −2.4, −2,2 × 2, 3, −2 × 3.5 , −1,22
Число 2222452122 четное или нечетное?
Последняя цифра — 2, а 2 — четное число. Итак, 2222452122 — четное число. □ _ \ квадрат □
Четное или нечетное — по математике для 2-го класса
Что такое четные или нечетные числа? Ключевые моментыЧетные числа можно разделить на две равные группы.
Нечетные числа нельзя разделить на две равные группы.
Посмотрите на эти примеры:
4 — четное число.
7 — нечетное число.
Вы заметили, как нечетные и четные числа чередуются с ?
1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10Больше десяти
🤔 Как узнать, является ли число больше 10 четным, и нечетным ?
👉 Посмотрите на место Ones. Помните, единица — это последняя цифра в числе.
Числа, которые оканчиваются на 0, 2, 4, 6 и 8 , равны даже .
Числа, которые оканчиваются на 1,3, 5, 7 и 9 , являются нечетными .
Например, подумайте о числе 13. Оно четное или нечетное?
3 на месте Единицы.
Итак, 13 — нечетное число.
Смотри и учись
Поздравляем! Теперь вы можете отличить четные числа от нечетных.
Начните практику ниже. 👇
Проверка четности или нечетности — математика для 3-го класса
Узнайте о четных и нечетных числах
Чтобы сыграть в баскетбол или футбол, вам нужно и даже игроков.
Что такое четные числа?
Четные числа можно разделить на две равные группы , например 2, 4, 6, 8 и 10.
6 игроков могут разделиться на две равные группы. Вот почему 6 — это число даже !
Что такое нечетные числа?
Любое число, которое не является четным , называется нечетным .
Нечетные числа нельзя разделить на две равные группы. 1, 3, 5 все нечетные.
Это четное или нечетное?
🤔 Как определить, четное или нечетное число из 10 ?
👉 Посмотрите на место Единственных.
Числа, заканчивающиеся на 0, 2, 4, 6 и 8, всегда равны , даже .
Числа, заканчивающиеся на 1, 3, 5, 7 и 9, всегда являются нечетными .
Подумайте о числе 13. Оно четное или нечетное?
Поскольку 3 — нечетное число, число 13 будет нечетным , тоже.
Правила сложения четных и нечетных чисел
Все числа соответствуют этим 4 образцам.
Четный + Четный = Четный
Пример: 2 + 2 = 4
Нечетный + Нечетный = Четный
1 + 3 = 4
Четный + Нечетный = Нечетный
2 + 3 = 5
Нечетный + Четный = Нечетный
1 + 2 = 3
Действительно ли эти правила верны для всех чисел? 🤔
Давайте попробуем на примере посмотреть.
Правила гласят, что сложение нечетного и четного должно дать нам нечетная сумма .
Проверим:
Да, сумма нечетная!
Правила вычитания
Как и в случае с сложением, существует 4 правила вычитания. Взглянем.
Четный — Четный = Четный
4-2 = 2
Нечетный — Нечетный = Четный
3 — 1 = 2
Четный — Нечетный = Нечетный
2-1 = 1
Нечетный — Четный = Нечетный
3 — 2 = 1
Давайте посмотрим на примере, чтобы убедиться, что эти правила верны.
Согласно правилам, вычитание двух нечетных чисел должно дать нам разницу в четных и .
Проверим:
Да, у нас есть разница в и даже !
Отличная работа! 🤗
Смотри и учись
🎉 Теперь вы можете отличить четные числа от нечетных. Начните свою практику ниже.
Как умножать нечетные числа
Пояснение:Допустим, у нас есть два числа, и их единицы — цифры и B соответственно.Если мы хотим узнать единичные цифры произведения и, все, что нам нужно сделать, это взглянуть на единичные цифры произведения и. Например, если мы умножим 137 и 219, то цифра единиц будет такой же, как цифра единиц. Поскольку единичная цифра 63 равна 3, единичная цифра 137 x 219 также будет 3. Короче говоря, нам действительно нужно беспокоиться только о единичных цифрах чисел, которые мы умножаем, когда мы пытаемся найти единичную цифру их произведения. .
Мы хотим найти единственную цифру.По сути, экспонента — это всего лишь короткая стрелка для повторного умножения. Давайте посмотрим на разряды первых нескольких показателей 2013 года.
— единица цифры 3.
Чтобы найти единичную цифру 2013 года во второй степени, нам нужно думать об этом как о произведении 2013 и 2013 годов. Как обсуждалось ранее, если мы хотим, чтобы единичные цифры двух чисел умножались вместе, нам просто нужно умножить их единичные цифры. Таким образом, если умножить 2013 год на 2013, то цифра из единиц будет такой же, как.
— единица цифра 9.
Далее мы хотим найти единичную цифру 2013 года в третьей степени. Для этого мы умножим квадрат 2013 года на 2013 год. Не имеет значения, что мы не знаем точно, чему равен 2013 квадрат, потому что нам нужно беспокоиться только о единичной цифре, которая равна 9. Другими словами, В 2013 году в третьей степени будет одна цифра, которая равна единице произведения 9 (которая была единицей в квадрате 2013 года) и 3 (которая является единицей цифры 2013 года).Когда мы умножаем 9 на 3, мы получаем 27, так что единица 2013 года в третьей степени равна 7.
— одна цифра 7.
Чтобы найти единичную цифру 2013 года в четвертой степени, нам нужно только позаботиться о том, чтобы умножить единичную цифру 2013 года в третьей степени (то есть 7) на единичную цифру 2013 года. Когда мы умножаем 7 и 3, мы получаем 21, что означает, что цифра 2013 в четвертой степени равна 1.
— одна цифра 1.
Чтобы найти единственную цифру 2013 года в пятой степени, мы умножим 1 на 3, что даст нам 3.
— единица цифры 3.
Обратите внимание, что мы вернулись к цифре из единиц с 3. Если мы умножим это на 2013, мы получим цифру из единиц 9. Другими словами, цифры из единиц повторяются в каждой четвертой степени.
Значение разряда степеней 2013 года следующее (с 2013 года в первой степени):
3, 9, 7, 1, 3, 9, 7, 1, ….
По сути, мы хотим найти 2013-й член приведенной выше последовательности. Обратите внимание, что каждый четвертый член равен 1, т.е.е. последовательность повторяется каждые четыре члена. Если позиция терминов в последовательности кратна 4, тогда термин будет 1. Короче говоря, 4-й, 8-й, 12-й, 16-й члены и так далее будут равны 1. Поскольку 2012 кратно 4, 2012-й член в последовательности будет равен 1. (Мы можем определить, кратно ли число 4, посмотрев на его последние две цифры.) Это означает, что 2013-й член будет 3. Таким образом, 2013 год в степени 2013 имеет одна цифра 3.
Ответ 3.
.


 29, 31.
29, 31. Эти два часа так и называются — время перестановки.
Эти два часа так и называются — время перестановки.